数字图像处理之直方图处理——a cute dog huang

关于图像处理的知识，确实很棒，在此感谢：https://blog.csdn.net/mary_0830/article/details/89003488

直方图处理概念
灰度级范围为[0,L-1]的数字图像的直方图是离散函数h（rk）=nk，其中rk是第k级灰度值，nk是图像中灰度为rk的像素个数。在实践中，经常用乘积MN表示的图像像素的总数除它的每个分量来归一化直方图，通常M和N是图像的行和列的维数。因此，归一化后的直方图由p（rk）=nk/MN给出，其中k=0,1,…,L-1。简单来说，p（rk）是灰度级rk在图像中出现的概率的一个估计。归一化直方图的所有分量之和应等于

1。在直方图中，暗图像集中分布在灰度级的低端；亮图像集中分布在灰度级的高端。低对比度图像具有较窄的直方图，且集中于灰度级的中部；高对比度图像的直方图分量则覆盖了很宽的灰度级范围。

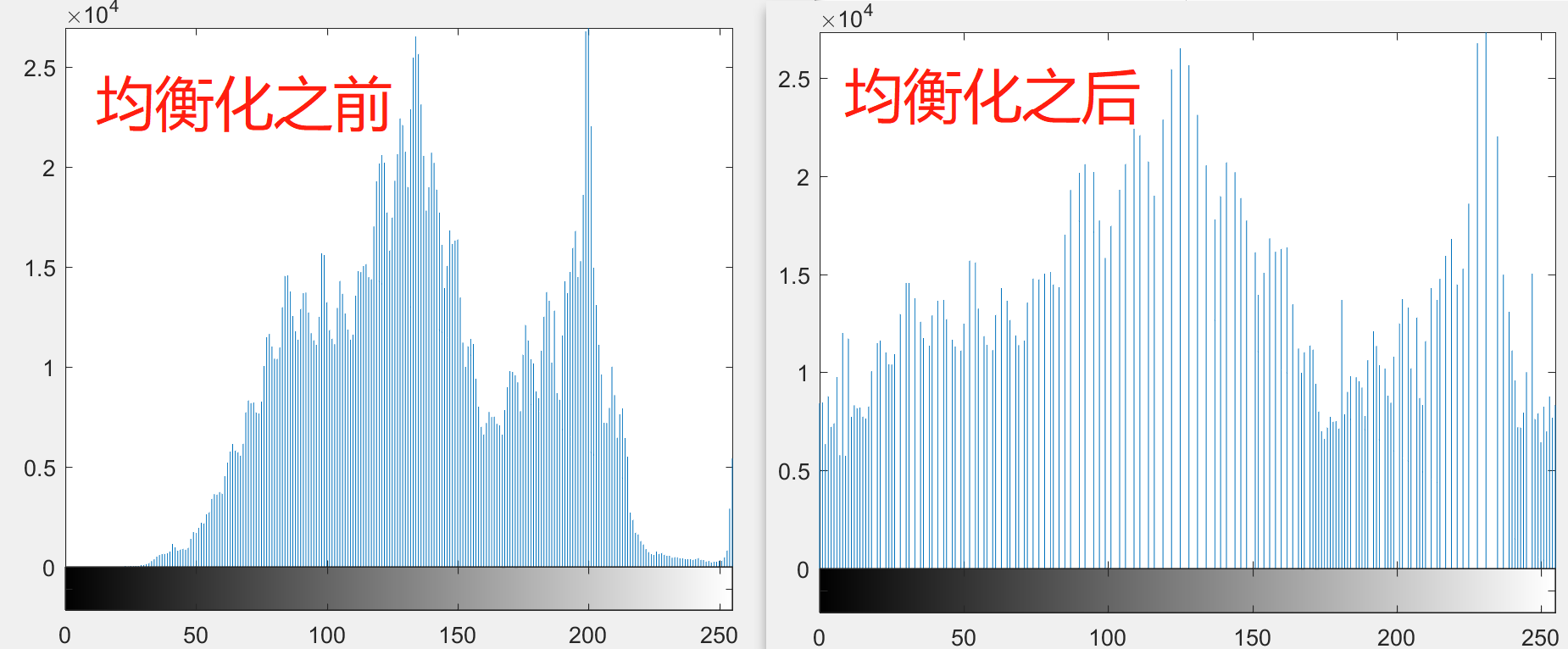
直方图均衡化（Histogram Equalization）

均衡化的基本原理：是把原始图的直方图变换为均匀分布的形式，这样就增加了象素灰度值的动态范围从而可达到增强图像整体对比度的效果。

均衡化步骤：

统计图像中每个灰度级出现的次数，计算图像中每个灰度级出现的概率；
根据变换公式得到直方图均衡化的变换函数；
根据变换函数映射到每个像素点；
输出映射后的图像；

、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、

clear all
f=imread('C:\Users\HUAWEI\Desktop\cute_dog_huang.jpg');
f=rgb2gray(f);
imshow(f);
imhist(f);
figure,imshow(f);
g=histeq(f,256);
figure,imhist(g);
figure,imshow(g);

、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、

 

 

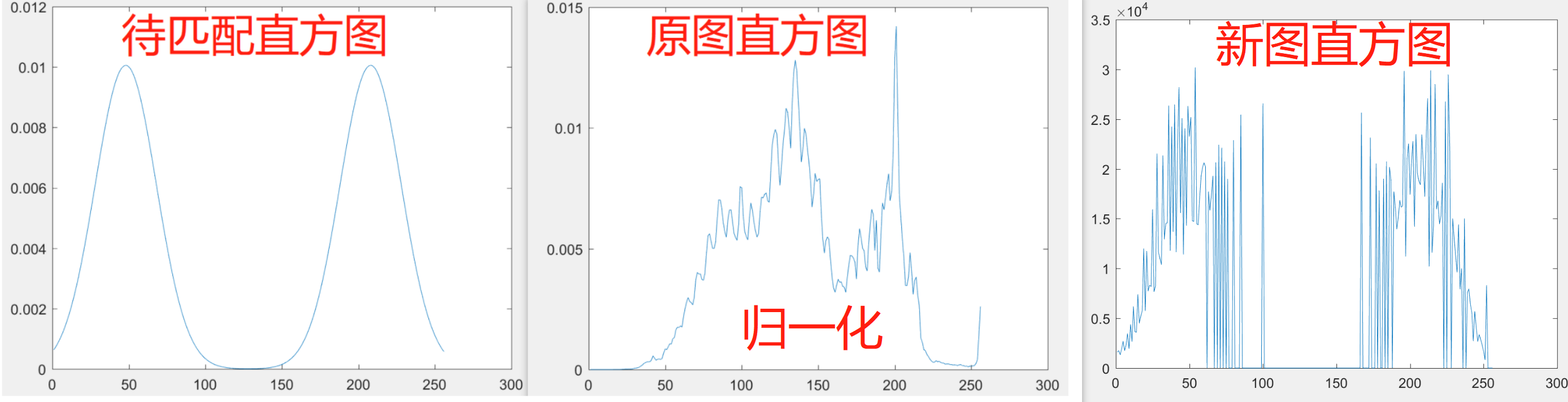
直方图规定化（Histogram Specification）

规定化的基本原理：有目的的增强某个灰度区间的图像，即能够人为地修正直方图的形状，使之与期望的图像相匹配。

规定化步骤：
计算给定图像的直方图pr®，并用它寻找直方图均衡变化，把sk四舍五入为范围[0，L-1]内的整数；
计算变化函数G的所有值，把变换函数G的值四舍五入为范围[0，L-1]内的整数，并将G的值放入一个表中；
对每一个值sk，使用步骤2存储的G值寻找相应的zq值，以使G（zq）最接近sk，并存储这些从s到z的映射。当满足给定sk的zq值多余一个时（即映射不唯一时），则选择最小的值；
首先对输入图像进行均衡，然后用步骤3找到的映射把该图像中的每个均衡后的像素值sk映射为直方图规定化后的图像中的相应zq的值，形成直方图规定化后的图像。
、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、

clear all
r=127;
x=-r:r+1;
sigma=20;
y1=exp(-((x-80).^2)/(2*sigma^2));
y2=exp(-((x+80).^2)/(2*sigma^2));
y=y1+y2; %双峰高斯函数，任意函数都可以

y=y/sum(y); %归一化，使函数符合概率分布的sum(y)==1这样一个规律
plot(y); %待匹配的直方图

G=[]; %函数的累积直方图
for i=1:256
G=[G sum(y(1:i))];
end

img=imread('C:\Users\HUAWEI\Desktop\cute_dog_huang.jpg');
img=rgb2gray(img);
[m n]=size(img);
hist=imhist(img); %待处理图像的直方图
p=hist/(m*n);
figure;plot(p) %原图直方图

s=[]; %待处理图像的累积直方图
for i=1:256
s=[s sum(p(1:i))];
end

for i=1:256
tmp{i}=G-s(i);
tmp{i}=abs(tmp{i}); %因为要找距离最近的点，所以取绝对值
[a index(i)]=min(tmp{i}); %找到两个累积直方图距离最近的点
end

imgn=zeros(m,n);
for i=1:m
for j=1:n
imgn(i,j)=index(img(i,j)+1)-1; %由原图的灰度通过索引映射到新的灰度
end
end

imgn=uint8(imgn);
figure;imshow(imgn)
figure;plot(imhist(imgn)) %新图的直方图

 、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、

 

 

 

局部直方图处理

 

在某种意义上，像素被基于整幅图像的灰度分布的变换函数修改。虽然这种全局方法适用于整个图像的增强，但存在这样的情况，增强图像中小区域的细节也是需要的。这些区域中，一些像素的影响在全局变换的计算中可能被忽略了，因为全局变换没有必要保证期望的局部增强。解决方法是以图像中每个像素的邻域中的灰度分布为基础设计变换函数。

前面描述的直方图处理技术很容易适应局部增强。该过程是定义一个邻域，并把该区域的中心从一个像素移至另一个像素。在每一个位置，计算邻域中的点的直方图，并且得到的不是直方图均衡化，就是规定化变换函数。这个函数最终用于映射邻域中心像素的灰度。然后，邻域中心的被移至一个相邻像素位置，并重复该过程。当邻域进行逐像素平移时，由于只有邻域中的一行或一列改变，所以可在每一步移动中，以新数据更新前一个位置得到的直方图。这种方法与区域每移动一个像素位置就计算邻域中所有像素的直方图相比有明显的优点。有时用于减少计算量的另一种方法是使用非重叠区域，但这种方法通常会产生我们不希望的“棋盘”效应。

 

-------在此几乎原文搬摘原文，只是为了学习，日后方便再次学习，感谢大佬。