SURF
Speeded-Up Robust Features (SURF)
本文提出了一种新的尺度和旋转不变检测器和描述符,即SURF (speedeup Robust feature)。SURF在可重复性、显著性和鲁棒性方面接近甚至优于先前提出的方案,
但可以更快地计算和比较。这是通过依赖积分图像进行图像卷积来实现的;通过构建现有检测器和描述符的优势(具体来说,为检测器使用基于Hessian矩阵的度量和基于分
布的描述符);并将这些方法简化到本质。这导致了新的检测、描述和匹配步骤的组合。
1. 介绍
寻找同一场景或物体的两幅图像之间的点对应是许多计算机视觉应用的一部分。图像配准、摄像机标定、
物体识别和图像检索只是其中的几个方面。离散图像点对应的搜索主要分为三个步骤。首先,“兴趣点”在图像中不同的位置被选择,比如角落,斑点,和丁字路口特征
点探测器最有价值的特性是它的可重复性。重复性是指在不同观察条件下寻找相同特征点的检测器的可靠性。然后用特征向量表示每个感兴趣点的邻域。该描述符必须是独特的,
同时鲁棒的噪声,检测位移和几何和光度变形。最后,对描述符向量进行匹配。匹配是基于向量之间的距离,例如马氏距离或欧氏距离。描述符的维数直接影响到所需的时间,
快速兴趣点匹配所需的维数更少。然而,低维特征向量通常没有高维特征向量那么明显。
我们需要在计算量与准确度之间平衡,能够在不牺牲性能的情况下快速计算。比如在简化检测方案的同时保持其准确性,以及在减少描述符的大小的同时保持其足够的独特性。
描述符的高维性通常是SIFT在匹配步骤上的一个缺点。对于只依赖普通PC的在线应用程序,这三个步骤(检测、描述、匹配)中的每一个都必须快速。
2、基于hessien矩阵的特征点
SURF特征点检测方法使用一个非常基本的Hessian矩阵近似。
2.1 基于hessien矩阵的特征点
我们为简化特征点检测,提高计算速度,使用盒滤波器近似(替代)Hessian矩阵。
黑塞矩阵(Hessian Matrix)是由一个多元函数的二阶偏导数构成的方阵,描述了函数的局部曲率,为了生成图像稳定的边缘点(突变点)。
对于一个图像I(x,y),其Hessian矩阵如下:
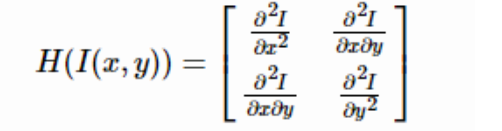
H矩阵的判别式是:
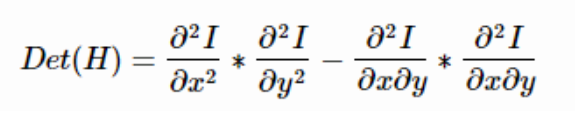
在构建我们使用的Hessian矩阵前需要对图像进行高斯滤波,在引入尺度后,给定图像I中一点X(x,y)。
X在尺度σ下的海森矩阵定义为H(X,σ)。经过滤波后的Hessian矩阵表达式为:
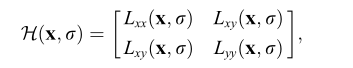
L(x,y,σ)=G(σ)∗I(x,y)代表着图像的高斯尺度空间,是由图像和不同的高斯卷积得到。
在离散数学图像中,一阶导数是相邻像素的灰度差:
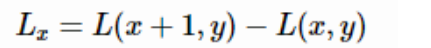
二阶导数是对一阶导数的再次求导:
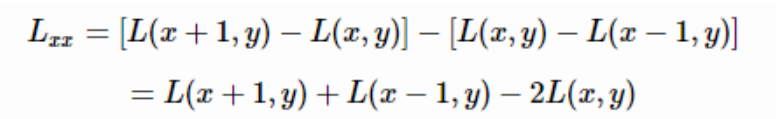
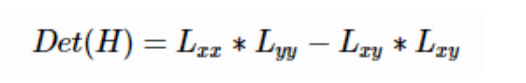
用这个值来判别图像局部特征点,Hession矩阵判别式中的L(x,y)是原始图像的高斯卷积核。
由于高斯核服从正太分布,从中心点往外,系数越来越小,为了提高运算速度,SURF算法使用了盒式滤波器(图2的右半部分)来替代高斯滤波器L,所以在L(x,y)
上乘了一个加权系数0.9, 近似的二阶高斯导数可以降低计算量。积分图允许用于盒型卷积滤波器的快速计算。
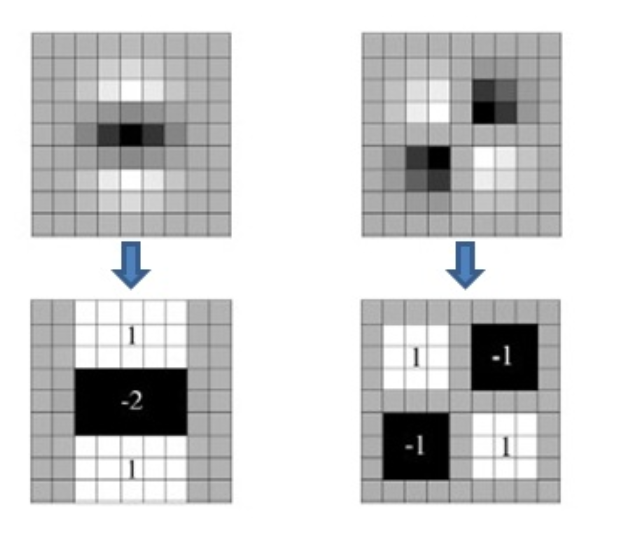
图2.从上到下:高斯二阶偏导数分别在y- (Lyy)和xy方向(Lxy)上;二阶高斯偏导数在y- (Dyy)和xy方向(Dxy)上的近似。灰色区域等于零。
在图2中9*9大小的盒滤波器近似σ=1.2的高斯函数,并且在图3中作为初始尺度层。为了提高计算效率,我们对矩形区域的权重保持简单化。
使用w=0.9。
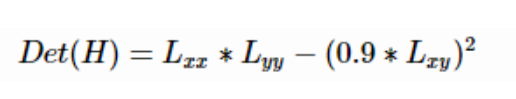
我们用Dxx 、Dyy和Dxy表示它们。近似的det(H)=DxxDyy-(w*Dxy)^2,对于权重我们定义为:
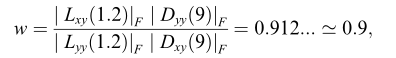
|x|F为弗洛比尼乌斯规范,权重随尺度的变化而变化。但在实践中,我们会保持这个因子为常数,因为对实验没有显著影响。
2.2、积分图像
为了使文章更加独立,我们简要讨论了积分图像的概念。他们允许用于盒型卷积滤波器的快速计算。在位置X=(x,y)处输入整数图像,
表示输入图像I中原点和X形成的矩形区域所有像素的总和。
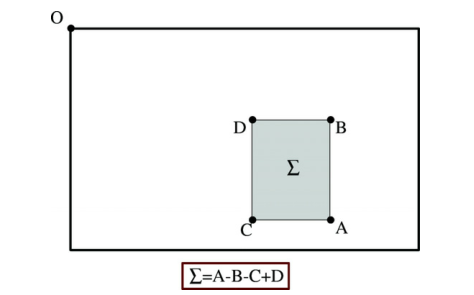
图1. 使用积分图像,它只需要三次加法和四次内存访问来计算一个矩形区域内的强度总和,任何大小
2.3、构造尺度空间
SURF算法的尺度空间由O组S层组成,同一组不同层图像之间尺寸一样,不同的是不同组间使用的盒式滤波器的模板尺寸逐渐增大,
Hessian的近似行列式表示图像中x位置的斑点响应。这些响应存储在不同比例的斑点响应图中
不同组间图像的尺寸都是一致的,不同的是不同组间使用的盒式滤波器的模板尺寸逐渐增大,
同一组不同层图像使用相同尺寸的滤波器,但是滤波器的尺度空间因子逐渐增大。如下图所示:
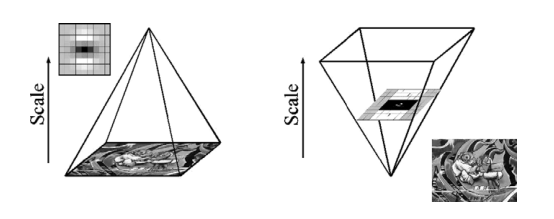
图3 与迭代地减小图像大小(左图)不同,使用积分图像允许以不变的成本(右图)提高过滤器的规模。
一个Octive是通过将相同的输入图像与一个增大的滤波器进行卷积而得到的一系列滤波器响应图。
对于两个连续的,我们必须将该大小增加至少2个像素(每边1个像素),以保持大小不均匀,从而确保中心像素的存在。这使得卷积核尺寸增加了6个像素(见图4)
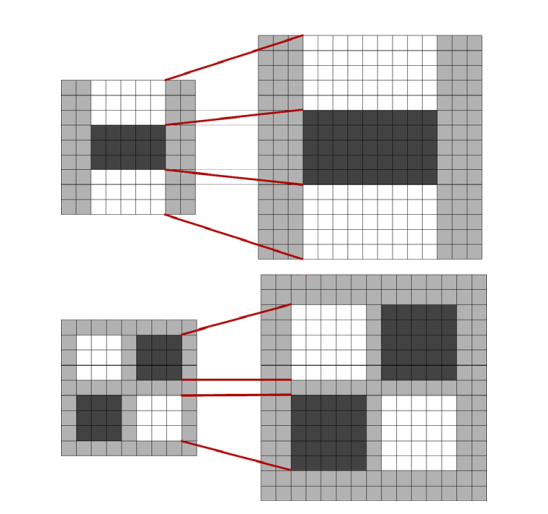
图4 过滤器Dyy(顶部)和Dxy(底部)为两个连续的尺度级别(9x9和15x15)。为了保证中心像素(顶部)的存在,暗部的长度只能增加偶数个像素。
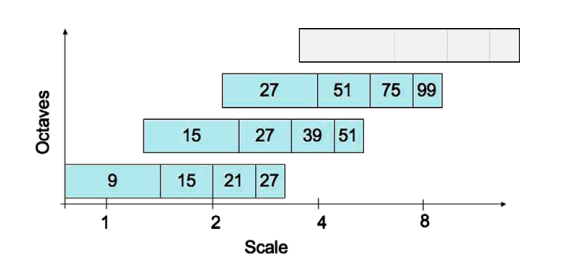
图5所示。三个不同的Octive滤波器边长度的图形表示。对数横轴表示尺度。为了无缝地覆盖所有可能的Octive,尺度是重叠的
2.4特征点检测
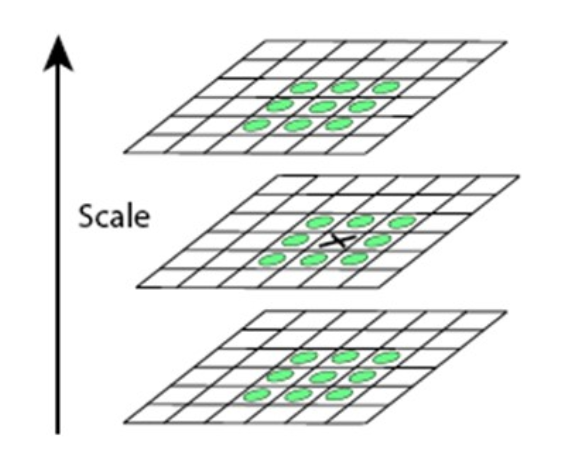
为了定位感兴趣的点在图像中的位置和尺度,一个非极大值抑制在3x3x3的空间邻域内比较极值。具体来说,利用SIFT的方法在尺度和图像空间中插值出Hessian矩阵行列式的极值。
3、特征点描述和匹配
根据特征点周围圆形区域的信息确定可重复的方向。然后,我们构造一个与选定方向对齐的正方形区域,并从中提取SURF描述符。
最后,对两幅图像进行特征匹配。下面将解释这三个步骤
3.1 特征点方向分配
在特征点的圆形邻域内,统计60度扇形内所有点的水平、垂直Harr小波特征总和,然后扇形以0.2弧度大小的间隔进行旋转并再次统计该区域内Harr小波特征值之后,最后将值最大的那个扇形的方向作为该特征点的主方向。
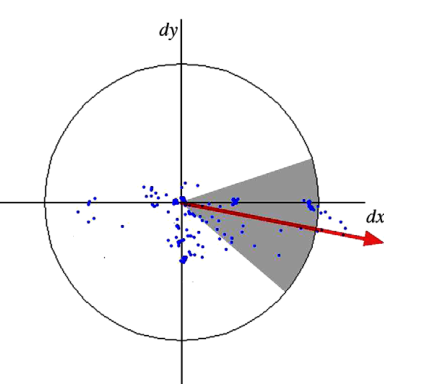
图6.方向分配:大小为60度的滑动方向窗口检测感兴趣点周围圆形邻域内每个样本点的高斯加权Haar小波响应的主导方向。
3.2 基于哈尔小波响应和的描述符
SURF算法中,提取特征点周围4×4个矩形区域块,所取得矩形区域方向是沿着特征点的主方向,而不是像SIFT算法一样,经过旋转θ角度。每个子区域统计25个像素点水平方向和垂直方向的Haar小波特征,这里的水平和垂直方向都是相对主方向而言的。
Harr小波特征为 水平方向值之和、垂直方向值之和、水平方向值绝对值之和以及垂直方向绝对之和
4个方向。该过程示意图如下:
一旦计算出小波响应并以高斯函数为中心对其进行加权,将响应表示为沿横坐水平响应强度标和垂直响应强度沿纵坐标的空间中的点。
为了简单起见,对于haar小波响应,水平方向上记dx,垂直方向上记dy小波响应。
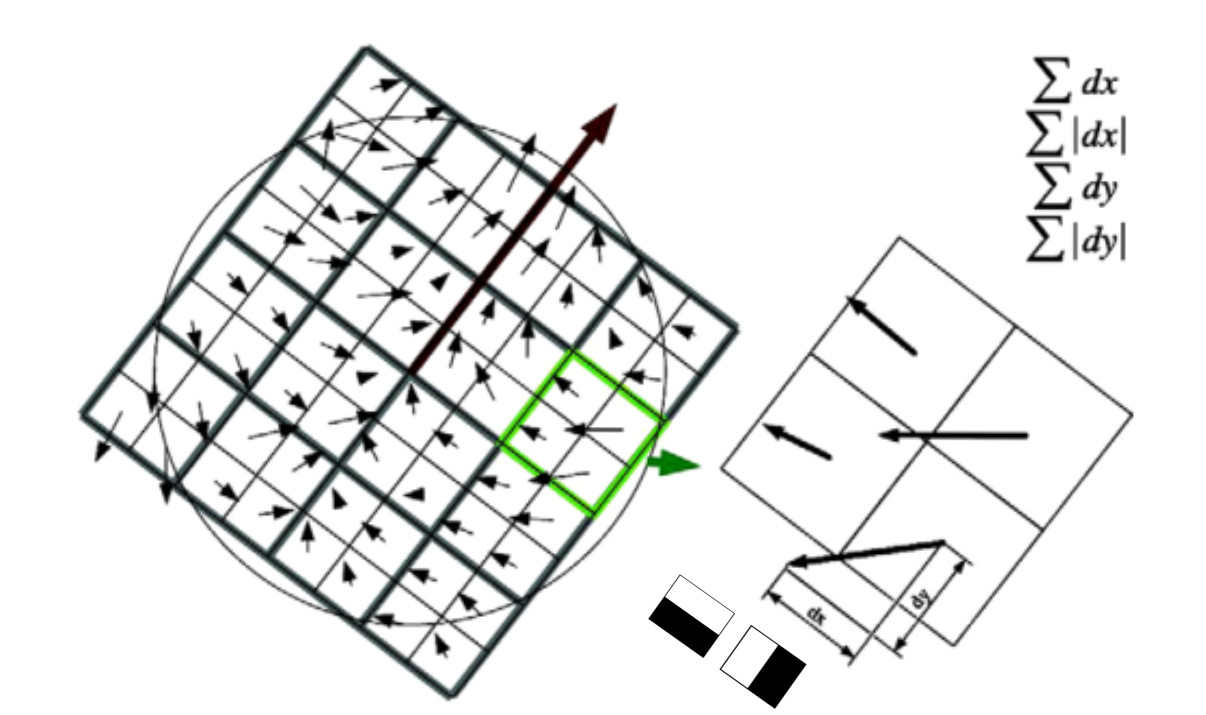
图7.为了构建描述符,一个由4x4个方形的子区域放置在兴趣点上(左边)。对于每个平方,小波响应由5x5个样本(为了说明,只展示了2x2个分区),Haar小波滤波器(黑色小块)计算x(左)和y(右)方向的响应。
对于每个域,收集dx |dx|;和|dy|,dy,相对于网格的方向计算(右)。将所有4x4个子区域连接起,结果得到长度为64的描述符向量。
图7显示的是子区域内三种不同图像强度模式的描述符的属性。我们可以想象这种是局部强度模式的组合,从而产生一个独特的描述符。
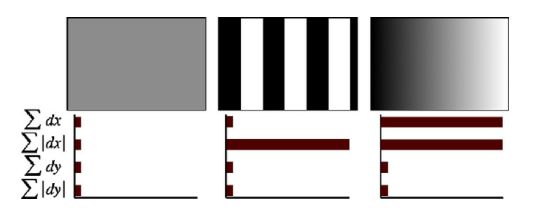
图7 子区域的描述符条目表示底层强度模式的性质。左:对于齐次区域,所有值都比较低。中:x方向存在频率时,dx值较高,其他均较低。当强度在x方向上逐渐增大时,dx和dy值都较高。
Harr小波特征
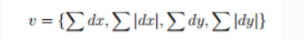
3.3 快速匹配索引
为了在匹配阶段进行快速索引,包含了底层兴趣点的Laplacian符号(即Hessian矩阵卷积的轨迹)。通常,特征点位于块状类型的结构中。
Laplacian的标志将深色背景上的亮斑与相反的情况区分开来。这个特性不需要额外的计算成本,因为它已经在检测阶段计算过了。在匹配阶段,我们只比较具有相同对比度的特征,
如图8所示。因此,这个最小的信息允许更快的匹配,而不降低描述符的性能。
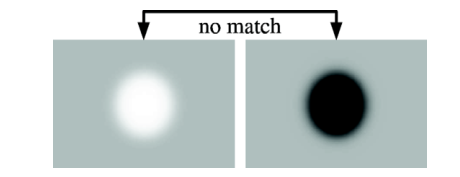
图八 如果两个特征点之间的对比度不同(浅色背景上的暗和深色背景上的亮),候选匹配点就不被认为是有价值的匹配。
https://www.cnblogs.com/mysunnyday/archive/2011/08/31/2160298.html 总结: SURF采用Henssian矩阵获取图像局部最值还是十分稳定的,但是在求主方向阶段太过于依赖局部区域像素的梯度方向,有可能使得找到的主方向不准确,后面的特征向量提取以及匹配都严重依赖于主方向,即使不大偏差角度也可以造成后面特征匹配的放大误差,从而匹配不成功;另外图像金字塔的层取得不足够紧密也会使得尺度有误差,后面的特征向量提取同样依赖相应的尺度,在这个问题上我们只能采用折中解决方法:取适量的层然后进行插值。




 浙公网安备 33010602011771号
浙公网安备 33010602011771号