商务统计学（三）第4、5章

商务统计学（三）第4、5章

 

《商务统计学》第七版

作者：戴维·莱文等，审校：胡大源

“先把书读厚，再把书读薄” --- 华罗庚

 

目录

• 商务统计学（三）第4、5章
  • 第四章 概率论基础
    • 4.1 概率论基础
    • 4.2 Further study
    • 4.3 贝叶斯定理
    • 4.4 计数规则
      • 计数规则1（可重复排列）
      • 计数规则2（一般性的可重复排列）
      • 计数规则3（全排列）
      • 计数规则4（选排列，排列）
      • 计数规则5（组合）
  • 第五章 离散概率分布
    • 5.1 离散变量
    • 5.2 二项分布
    • 5.3 泊松分布

 

第四章 概率论基础

4.1 概率论基础

• 概率论是连接描述统计与推断统计的桥梁

概率

• 概率，表示机会大小的数值，可分为三种
  • 先验概率，根据有关事件发生过程预先掌握的知识来推测的事件发生的概率
  • 经验概率，对观测数据使用统计调查方法得出的概率
  • 主观概率，顾名思义，主观

事件

• 概率论的基本着眼点就是研究变量可能出现的单个结果，每种可能的结果被称为一个事件
  • 仅仅由一个特征描述的事件被称为简单事件，比如硬币的正反面，对应有简单概率
  • 两个或两个以上特征的事件，联合事件，对应有联合概率

样本空间

• 可能发生的事件的集合
• 样本空间的表示方法，列联表，韦恩图

边缘概率

• 边缘概率由联合概率组成。
  \[例如，事件B包含事件B_1和B_2，那么事件A发生的概率是，A与B_1同时发生的联合概率和A与B_2同时发生的联合概率的和\\ 此处，P(A)=P(AB_1)P(AB_2)，（前提是B_1，B_2是互斥且完备的事件 \]

互斥与完备

• 互斥：两个事件不可能同时发生，两事件的韦恩图没有重叠部分

  • 互斥与独立不同！！！是两个概念

  • \[若AB互斥，P（A|B）= 0 \neq P(A)，因此AB互斥但不相互独立\\ 这说明互斥和独立是可以同时发生的 \]

• 完备：一组事件中必发生其一，该组事件中的所有事件的韦恩图会填满整个样本空间

 

4.2 Further study

一般加法法则

• \[P(A\cup B)=P(A)+P(B)-P(A\cap B) \\ 一定去除重复的部分 \]

 

条件概率

• \[P(A|B)=\frac{P(A\cap B)}{P(B)} \\ 想想韦恩图，其实就是AB相交部分再B中所占的比例，同理\\ P(B|A)=\frac{P(B\cap A)}{P(A)}=\frac{P(A\cap B)}{P(A)} \]

• 还可以用（手工）决策树的形式展示每种可能的条件概率

 

一般乘法法则

• 对条件概率变形就得到了乘法法则
  \[P(A\cap B)=P(A|B)*P(B)\\ 我们可以用它来计算AB交集在整个样本空间的占比 \]

 

独立性

• 一个事件的结果不会对另一个事件造成影响

• 判断独立性的两种方法：

  \[当且仅当P(A|B)=P(A)时，两事件相互独立 \]

  2.将上述独立性的定义代入乘法法则得到的公式也是一种判断独立性的方法

  \[当且仅当P(A\cap B)=P(A)*P(B)时，两事件相互独立 \]

• 互斥与独立不同！！！是两个概念

• \[若AB互斥，P（A|B）= 0 \neq P(A)，因此AB互斥但不相互独立\\ 这说明互斥和独立是可以同时发生的 \]

 

独立事件的乘法法则

• \[P(A\cap B)=P(A)*P(B)其实就是独立事件的乘法法则\\ 你想嘛，乘法法则被代入了两事件相互独立的公式 \]

 

一般乘法法则计算边缘概率

• \[由 P(A)=P(A\cap B_1)+P(A\cap B_2)+P(A\cap B_3)+...+P(A\cap B_n)，B_1，B_2,B_n表示n个互斥且完备的事件\\ 被代入一般乘法法则\\ P(A \cap B) = P(A|B)*P(B)\\ 得\\ P(A)=P(A|B_1)P(B_1)+P(A|B_2)P(B_2)+...+P(A|B_n)P(B_n) \]

 

4.3 贝叶斯定理

托马斯贝叶斯将我们学过的条件概率延伸为贝叶斯定理

• 将条件概率的分子用一般乘法法则替换，将分母用边缘概率替换，就得到贝叶斯公式

  \[由P(B|A)=\frac{P(A\cap B)}{P(A)}=\frac{P(A|B)*P(B)}{P(A)}\\ P(A)=P(A\cap B_1)+P(A\cap B_2)+P(A\cap B_3)+...+P(A\cap B_n)，B_1，B_2,B_n表示n个互斥且完备的事件\\ 得\\ P(B_i|A)=\frac{P(A|B_i)*P(B_i)}{P(A\cap B_1)+P(A\cap B_2)+P(A\cap B_3)+...+P(A\cap B_n)}，i表示n个互斥且完备的事件中的第i个事件 \]

• 关于贝叶斯公式的应用也是很关键的一步

 

 

4.4 计数规则

事件的概率是该事件可能发生的结果数除以所有可能发生的结果总数。但分母上的“所有可能发生的结果总数”有时候很难准确计算，因此需要利用前人总结出来的计算规则来计算”总数“

计数规则1（可重复排列）

事件的完成分为n个步骤，每一步有k个不同的互斥且完备的结果可能发生，那么可能发生的结果总数为

\[k^n \]

计数规则2（一般性的可重复排列）

该规则是对规则1的延伸，它允许在事件完成的各个步骤有不同的数量结果， 因此可能发生的结果总数为

\[k_1*k_2*k_3*...*k_n \]

计数规则3（全排列）

计算一组物品有多少种不同的排序方法

\[n个物品不同的排列总数为：n！ \]

计数规则4（选排列，排列）

顾名思义，选择n个物品中的x个，并对这x个进行排列，不同排序的总数为：

\[P_x=\frac{n!}{(n-x)!} \]

计数规则5（组合）

有时候并不需要考虑顺序，现在在不考虑顺序的情况下，从n个物品里选出x个，不同的组合数为;

\[C_x=\frac{n!}{x!*(n-x)!} \]

我们可以看到，相比于排列，组合多除了x!，其实这个x!就是本来选出的x个物品的不同顺序的排序，但因为在组合中不考虑顺序问题，因此除去x!

 

---

 

第五章 离散概率分布

数值变量是代表数量的变量，数值变量分为离散和连续两类。连续数值是来自测量的结果，离散数值是来自计数的结果。本章主要讨论离散数据变量

5.1 离散变量

• 离散变量的概率分布

  小标题是指变量可能出现的互斥结果的取值以及对应概率的列表（就是第一列是所有可能的取值，第二列是对应的概率）

• 离散变量的期望值

  离散变量概率分布的均值就是它的期望值 --- 每个可能的结果 xi乘以它相应的概率P(X=xi)，然后加和

  \[\mu=E(X)=\sum_{i=1}^{N} x_iP(X=x_i) \]

• 离散变量的方差

  每一个可能出现结果的离差平方[Xi-E(X)]^2乘以对应的概率

  \[\sigma^2=\sum_{i=1}^{N} [x_i-E(X)]^2P(X=x_i) \]

• 离散变量的标准差

  对方差开方喽

 

5.2 二项分布

本节和下节将研究数学模型。数学模型是对我们关注的一个变量的数学表达，有了数学模型后就可以精确地极端这个变量发生任意结果的概率。

我们称离散变量的数学模型为概率分布函数。

二项分布的基本特征

• 样本包含n个固定数目的观测值，观测值相互独立

• 这些观测值可以分为两类，且这两类具有互斥性和完备性

  

二项分布的期望值

\[\mu=E(X)=np \]

二项分布的方差

\[\sigma=np(1-p) \]

 

5.3 泊松分布

机会域：许多研究都基于在一个特定的时间或空间内，这就是机会域，通常由时间，长度，表面积等来定义

what

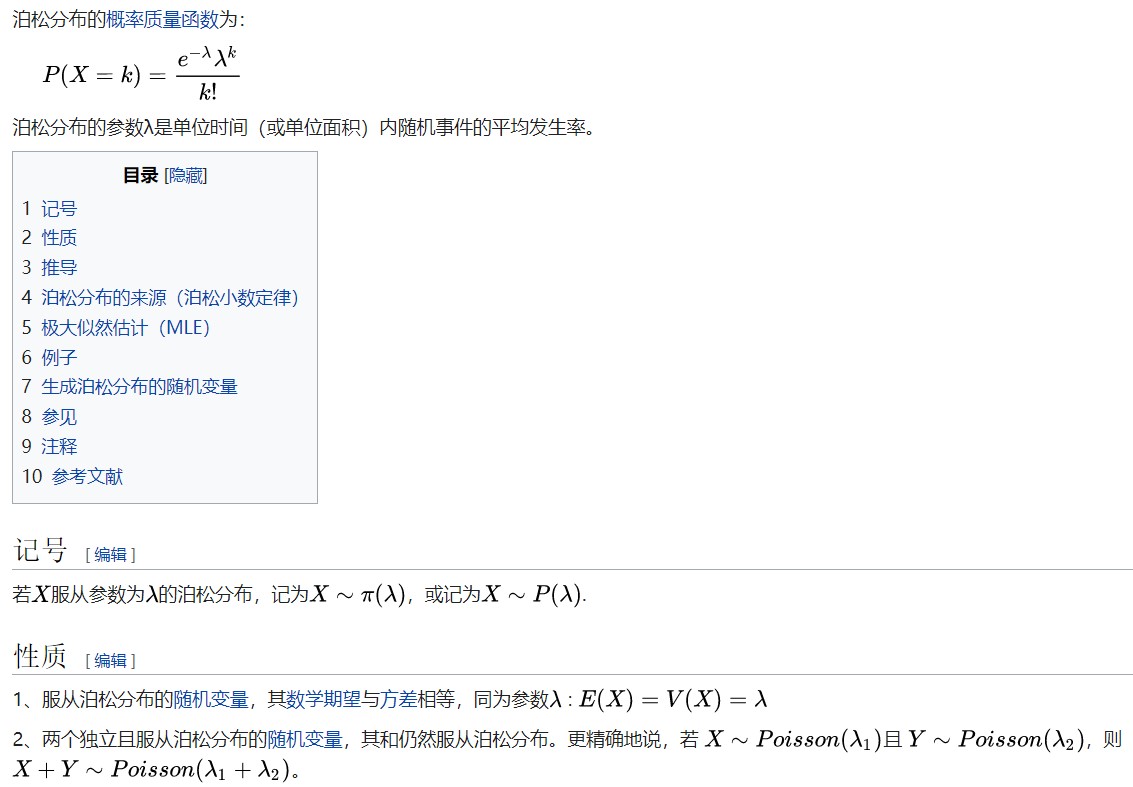
公式中参数lambda表示均值，或单位机会域中期望的事件发生的数量，泊松分布的方差也等于lambda

泊松随机变量的取值区间也就是事件发生数量X的取值范围，可以从0到正无穷

还有个常用的性质：

\[P(X>2)=P(X=3)+P(X=4)+...=1-P(x<=2)=1-P(X=0)-P(X=1) \]

什么时候使用泊松分布计算事件发生的概率L

• 在给定的机会域中（时间、长度、表面积等），你想知道某一时间发生的次数
• 一个事件在整个机会域中都是一样的
• “在某机会域中事件发生的数量”与“其他任何机会域中的事件发生的数量”相互独立
• 随着机会域变小，在某个机会域中两个或两个以上事件发生的概率近乎于0

例如，一天中进入银行的人数，每月的损耗量等