商务统计学(二)第2、3章
商务统计学(二)第2、3章
《商务统计学》第七版
作者:戴维·莱文等,审校:胡大源
“先把书读厚,再把书读薄” --- 华罗庚
第二章 整理并使变量可视化
- 我们首先要确定变量是属性变量还是数值变量,以便选择不同的方法整理数据并实现可视化
2.1 整理属性变量
- 总结表
- 列联表 --- 两个属性变量交叉分类列表
- 基于计数
- 基于总和百分比
- 基于行和百分比
- 基于列和百分比
2.2 整理数值数据
- 有序数组 --- 排序
- 频数分布 --- 把数值变量的值划分到按照数值顺序排列的组中
- 频数分布应包括5到15个组,组距=(最大值-最小值)/ 组数
- 每个值必须被包含在某个组中,且只能分配到一个组中
- 每组包含一个互斥的值的范围,叫做组间。
- (simple,就像小时候画直方图计算的那些)但频数分布相同的频数实际侧面表示着两个非常不同的比例,因此引出了频率分布和百分比分布
- 频率分布和百分比分布
- 频率分布 --- 每组占总数的频数(小数)
- 百分比分布 --- 每组占总数的百分比
- 累积(百分比)分布
- 它提供了一种方式来展示少于一个特定值的观测值所占的百分比(也就是之前累积过的数值在后面会继续被用于加和,此所谓累积)
2.3 属性变量的可视化
- 条形图(bar chart)
- 如果要在各类别之间进行比较,首选条形图
- 饼图(pie chart)
- 如果观察各类别在整体中所占比例,首选饼图
- 帕累托图(Pareto chart)
- 如果数据集中在少数几个类别,首选帕累托图
- 把每一类别的数据按照其频数的大小递减排列,并以此顺序做出柱状图,然后在同一图添加上累计百分比线
- 该图得名与“帕累托原则”,“属性变量“的少数几个类别代表了数据的大部分,而其他很多类别值代表数据相对较小甚至微不足道的部分”
- 因此,帕累托图可以帮助你从“众多微不足道的”类别中识别出“最具决定性的”几个类别。当收集数据的目的是发现缺陷或不规范之处时,帕累托图是行之有效的工具
- 在某些情况下,需要设置名为“其他”或“杂项”的类别,一般放在横轴的最右侧
- 对比条形图(side-by-side bar chart)
- 善于比较若干个属性变量在某方面的不同,该方面中可能又会分为几类,因此每个属性变量可能包含还几个不通过含义的柱状图
2.4 数值变量的可视化
- 茎叶图(stem-and-leaf display)--- 清楚地展示数据是如何分布的
- 直方图(histogram)--- 表示每组观察值的频数或百分比
- 百分比多边形图(percentage ploygon)--- “标注各组组中点(横轴的值就是每组的中点)和该组的百分比并将这些点连接对应起来”,和直方图一样,它也展示数据的分布情况
- 累计百分比多边形图(累计曲线图)(cumulative percentage ploygon) --- 累计百分比的好处就是,我们可以更加直观地看出小于或者大于横轴某个值的那些值占总体的百分比
2.5 两个数值变量的可视化
- 散点图(sactter plot)--- 将一个变量放在X轴一个变量放在Y轴,以此来检查两个数值变量之间的额相关性 --- 正/负相关,弱关联,或者是没有关系
- 时间序列图(time-series plot)--- 用来研究数值变量随时间变化的联系(原来常用的销售额啊等等都称为时间序列图)
2.6 一组变量的整理和可视化
从2.1到2.5,讨论的都是一个或两个的数值变量所使用的简单方法。当需要面对三四个或者一组变量时,我们要采用本节所讨论的方法,这些方法不如简单的方法精确,所以常用于获取一组数据的初步结论而不是取代2.1到2.5的方法。
-
多维列联表(multidimensional contingency table)--- 记录观测值,或许可以从中发现“潜在变量”---影响其他属性。例如,在由基金类型和风险的总百分比的列联表的基础上加入市值(可分为大中小三种不同市值)这一类型,就可以产生一个多维列联表。
- 而基金类型和风险水平的关系明显受到市值的影响,市值就是之前没有发现的一个“潜在变量”
- Excel透视表可以互动地改变总结的层级和变量的排列与格式
- 也可以在多维列联表中加入数值变量,例如,计算每个由基金;类型、风险和市值构成的组的10年平均收益率
-
数据发现(data discover)
-
向下钻取(drill down)--- 从最高层面的总结向下展开数据挖掘
-
有些数据发现主要靠可视化,比如树状图(当然,树状图并不一定是树形,根据占比和类型使用不同大小与颜色,展现不同大小和颜色的矩形块,就像好用的SpaceSniffer那样)
-
2.7 变量整理与可视化中的挑战
在进行数据可视化的过程中,我们必须意识到不参与制作的读者往往难以理解对数据复杂的总结,甚至让人产生错误的印象,使分析无法取得成效。挑战就是如何将可视化变得简练且易懂,且避免上述问题
- 朦胧数据:信息过载,细节过多,会导致数据朦胧从而妨碍数据决策。
- 造成错误印象:
- 不同颜色和顺序排列的饼图会给人不同的感觉
- 起点不是原点的轴,或者缺少中间值的“断层轴”也可能导致错误的印象
- 花哨图表:理工科的人大概都不会怎么喜欢太过花哨的图表,鲜明的颜色区分和合适的展示构图远远比花哨的图表更有助于分析。当然,用于展示的“海报式”图表除外。
第2章小结
整理与数据可视化属于DCOVA框架的第三层和第四层,完成它们取决于变量的类型(数值还是属性)、以及变量的个数(个人认为,还要有对使用哪种图表、如何展示数据(颜色、顺序等)的选取)

数据整理和可视化有助于总结数据。对于数值数据而言还有很多方法可以用来概括总结数据 --- 数值描述性度量就是最常见的例子,见下一章。
第三章 数值描述度量
在描述数值变量时,第2章讨论的总结方法仅仅是开始,我们还需要使用有助于描述这些变量的集中趋势、变异程度和分布形状的方法
- 集中趋势 --- 某个数值变量在一个典型值或中心值周围的集中程度
- 变异程度 --- 距离数值的中心值的离散(分散)程度
- 分布形状 --- 观测值从最低值到最高值的分布情况
- 以及,两数值变量之间联系的紧密程度 --- 协方差和相关系数
3.1 集中趋势
某个数值变量在一个典型值或中心值周围的集中程度
-
集中趋势的三种度量方式
平均数、中位数、众数
-
算数平均数(arithmetic mean)(均值,mean)
\[\bar{a_n}=\sum(a_n)/n \]等同于样本均值(sample mean)
- 均值可以表示一组数据的典型值或中心值(就像这组数据构成的跷跷板的平衡点一样)
- 但也因为均值是所有观测值发挥相同作用的度量,因此很容易受极值的影响。存在极值是应避免使用均值作为唯一的度量方式
- 如何快速判断均值是否被极值影响?可以观察均值在该组数据中的位置,如果均值与中心或者中间的位置偏离很大,那么很可能是被极值所影响,且说明此时极值不是一个好指标
-
中位数(median)
\[中位数=按大小排列在第(n+1)/2位的观测值 \]- 奇数个观测值,则中位数为中间位置的观测值
- 偶数个观测值,则中位数为中间两个观测值的算数平均值
- 中位数不易受极值的影响
-
众数(mode)
- 一组观测值中有可能没有众数 --- 每个值出现的次数都相同 --- 没有哪个数值是最典型的
- 众数不易受极值的影响
3.2.1 变异程度
距离数值的中心值的离散(分散)程度
- 全距:最大观测值与最小观测值之差
- 全距衡量一组数据的总的离散程度
- 但全距没有考虑在这个范围内,数据是如何分布的,因此当数据中至少存在一个极值时,使用全距度量有可能造成误解
标准差与方差:
都统计样本观测值在均值周围的“平均”离散程度 --- 较大值是如何在它之上波动的,较小值是如何在它之下波动的
结果总是>=0,只有样本中的每个值都一样时,标准差和方差才为0
-
总体方差:
-
\[S^2 = \frac{\sum(X_i-\bar{X})^2} {n} \]
-
-
样本方差:
-
\[S^2 = \frac{\sum(X_i-\bar{X})^2} {n-1} \]
-
PS.分子部分学术名叫做“离差的平方和”,而一组数据的离差的和总是为0(因为都是与均值之间的差,而均值是“跷跷板的平衡点”)
-
-
总体标准差:
-
\[S = \sqrt{S^2} = \sqrt{\frac{\sum(X_i-\bar{X})^2} {n}} \]
-
-
样本标准差:
-
\[S = \sqrt{S^2} = \sqrt{\frac{\sum(X_i-\bar{X})^2} {n-1}} \]
-
求得样本方差S,就表示,这个样本中的数据(大部分)聚集在
\[[\bar{X}-1S , \bar{X}+1S] \]之间,当然并不是说所有的数据都一定在这个范围内
-
除以n还是除以n-1与统计推断和样本分布属性有关**,随着样本容量的增加,除以n和除以n-1的差异会逐渐变小。在实践中你最有可能使用样本标准差作为变异程度的度量指标
-
变异系数(coefficient of variation):
-
变异系数等于标准差除以均值再乘以100%
\[CV = (\frac{S}{\bar{X}})*100\% \] -
变异系数表示度量数据相对于均值的离散程度,它总是与用百分比表示而不是像变异程度用数值表示
-
变异系数更擅长于比较两种或者多种不同度量单位的数据。比如,“不同的麦片之间是每单位的卡路里的差异大,还是每单位含糖量的差异大”,计算两个CV值,CV大的说明该种度量单位的差异大
-
-
Z值(Z score):
-
Z值等于观测值减去均值再除以标准差
\[Z = \frac{X_i-\bar{X}}{S} \] -
Z值表示观测值高于或者低于标准差的倍数。Z为正则观察值高于标准差,Z值为负则低于标准差,Z值为0则观察值等于均值,Z值大于+3.0或者小于-3.0则说明观察值为异常值(outlier)
-
3.2.2 分布形状
观测值从最低值到最高值的分布情况
-
偏度(skewness):根据均值和中位数衡量数据围绕均值不对称分布的情况
-
左偏分布,负偏,均值<中位数
-
零偏度,对称,均值=中位数
-
右偏分布,正偏,均值>中位数
-
要格外注意他们的形象化表示:
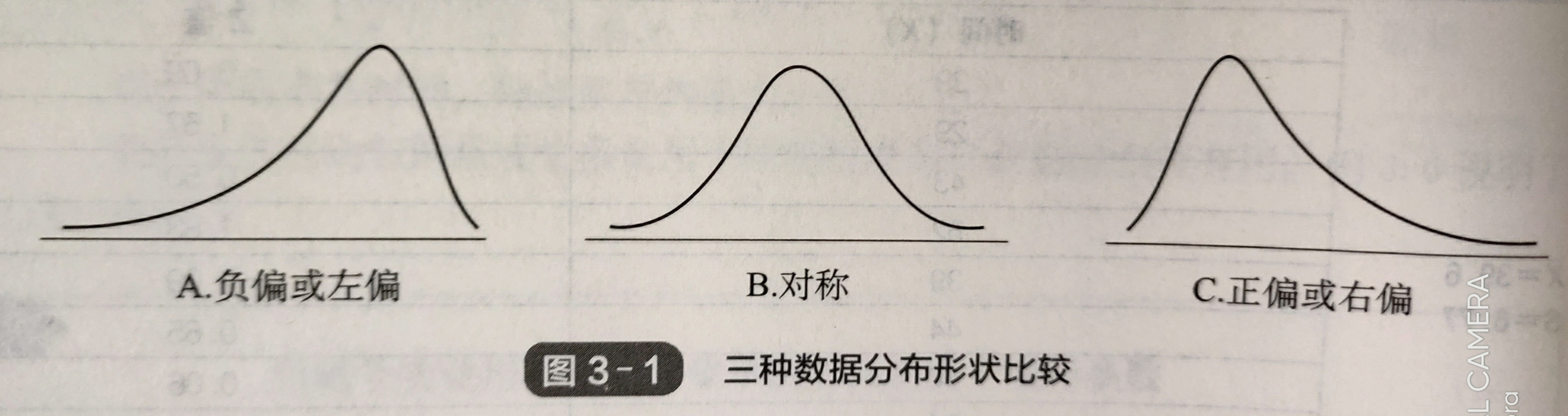
比如说左偏,它的形象化表示其实是在图表的右侧凸起。这是因为凸起表示数据的分布情况,表示在左偏时大部分数据都大于均值(默认向右数轴变大)
-
-
峰度(kurtosis):衡量分布曲线顶尖部分的形状 --- 也就是说曲线如何向分布的中心聚集。
- 峰度将“钟型正态分布”(的顶部)的峰度定义为0
- 具有比钟型分布更尖锐的尖顶的分布时,峰度大于0,被称作“尖峰(lepokurtic)”
- 具有比钟型分布更平缓的分布时,峰度小于0,被称作“低峰(platkurtic)”
-
与正态分布相比,尖峰分布的观测值更多的集中在均值附近,而低峰分布更少
-
观测值在均值附近的集中程度不仅影响中心顶点的形状,也影响尾部(分布曲线的末端)。与正态分布相比,尖峰分布的尾部更平,有更多的观测值
-
小结上述两点就是“尖峰厚尾”,是有前提的

-
如果尖峰分布被误认为正态分布,那么决策时就会低估极端值。
3.3 探索数值数据
我们还可以通过以下方法对数值变量的分布加以分析
-
四分位数(quartiles)
-
第一四分位数:
\[Q_1 = 第\frac{n+1}{4}个从小到大排序的观测值 \]以此类推,第二四分位数:
\[Q_2 = 第\frac{2*(n+1)}{4}个 \]第三四分位数:
\[Q_3=第\frac{3*(n+1)}{4}个 \]。。。
-
如果Q为整数则取对应位置观测值,如果Q在两个位置之间(n.5)则取两个数均值,如果Q在两个位置之间则对Q进行四舍五入,就近取数
-
对应的,还有百分位数(percentiles)可以让我们取任意位置的数。
-
-
四分位距(interquartile range or midspread),第三四分位数与第一四分位数之差
\[四分位间距 = Q_3-Q_1 \]- 四分位距没有考虑小于Q1和大于Q3的数据,因此不易受极端值影响
- 描述性统计量中,中位数,Q1,Q3和四分位距都不易受极端值影响,被称为“抗干扰度量”
-
五值概括法(five-number summary)
-
它是确定分布形状的一种分析方法
-
五值概括法中包括,最小观测值,第一四分位数,中位数,第三分位数和最大观测值
-
如何通过五个数值判断分布情况:

注:三种判断的结果都指向时才允许得结论。如果是两个指向左偏,一个指向右偏,那么此时无法得出结论
-
-
箱线图(boxplot,盒须图)是五值概括法的可视化表现形式
-
矩形盒子的中垂线表示中位数,矩形左侧边线对应Q1,右侧边线对应Q3,矩形的水平分割线延伸至矩形外,线的两端分别对应X最小和X最大
-
既然密度曲线和箱线图都是对分布情况的可视化,那么他们之间自然可以对应起来

-
总体数值描述度量
-
总体均值,计算公式与样本均值一样
-
总体方差、总体标准差,除以N而不是样本方差或样本标准差的n -1
-
经验法则(empirical rule),是指对于构成正态分布的总体数据
-
\[约有68.26\%的观测值会在(\mu-1\sigma,\mu+1\sigma)的范围内 \]
-
\[约有95.44\%的观测值会在(\mu-2\sigma,\mu+2\sigma)的范围内 \]
-
\[约有99.73\%的观测值会在(\mu-3\sigma,\mu+3\sigma)的范围内 \]
-
在三个标准差区间外的数据几乎可以确定为异常值
-
对于大多数数据集,大部分观测值会集中在均值附近。但对于
- 左偏的数据集(均值小于中位数,凸起在右),观察值集中在中位数右侧,亦大于均值
- 右偏的数据集(均值大于中位数,凸起在左),观察值集中在中位数左侧,亦小于均值
-
如果数据集较为接近钟型分布,经验法则则会更精确地反应“数据更多地集中在均值附近”的这一特征
-
-
切比雪夫法则(Chebyshev rule) ,对于分布“很偏”的数据集,我们应使用切比雪夫法则而不是经验法则
\[无论分布形态如何,位于偏离均值k个标准差范围内的观测值的百分比至少为(1-\frac{1}{k^2})*100\%\quad(k\geq1) \]- 当k=2,则可以得出,至少有75%的观测值在距离均值2个标准差的范围内
- 切比雪夫法则适用于任何分布
-
上述两种方法都可以用来理解数据是如何围绕均值分布的。一般都只能通过样本数据来进行推断,样本统计量为
\[(\bar{X},S) \]而如果使用的是所有数据进行分析,(要么数据量本身少,要么使用大数据处理技术)那么总体统计量表示为
\[(\bar{\mu},\sigma) \](rigorous)
3.5 协方差与相关系数
两个数值变量之间的度量方法
-
协方差(covariance)
-
样本协方差(sample covariance)
\[cov(X,Y)=\frac{\sum_{i=1}^{n}(X_i-\bar{X})(Y_i-\bar{Y})}{n-1} \] -
协方差可以有任何值,因此无法只根据协方差的计算结果说明是强关系还是弱关系,为了更好地判断关系的强弱,还需要计算相关系数
-
-
相关系数(coefficient of correlation),衡量两个数值变量之间的线性关系强度
-
样本相关系数
\[r=\frac{cov(X,Y)}{S_xS_y}\\ S_x=\sqrt{\frac{\sum_{i=1}^{n}(X_i-\bar{X})}{n-1}}\\ S_y=\sqrt{\frac{\sum_{i=1}^{n}(Y_i-\bar{Y})}{n-1}} \] -
总体相关系数
\[总体相关系数用\rho表示 \] -
相关系数的值域为(-1,+1),(毕竟“系数”)
-
完全相关是指代表观测值的散点都在一条线上
-
两个变量之间的三种不同关系
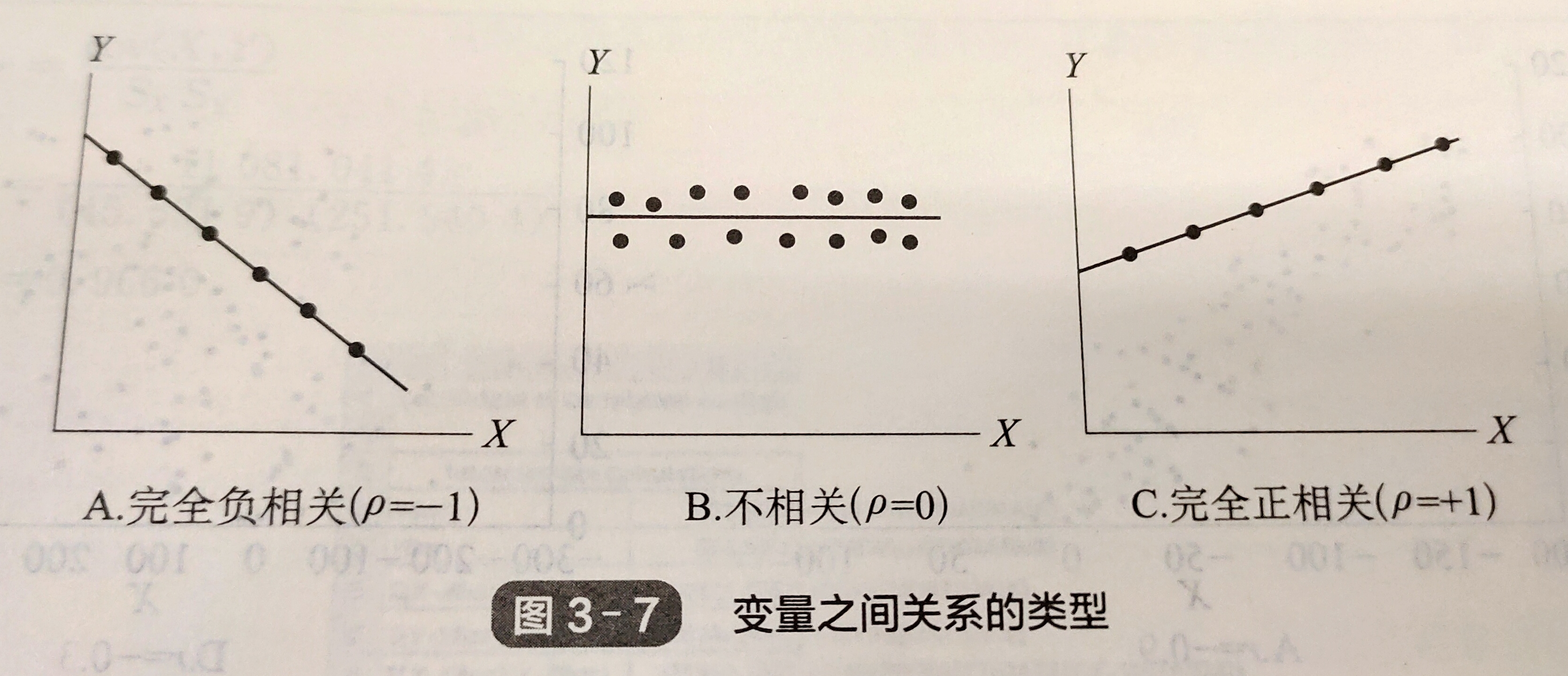
仅有相关性无法证明变量之间存在因果关系 --- 一个变量的变化导致另一个变量的变化。
强相关性也可能是偶然的。有可能的确是因为因果关系,也有可能的确是因为没有考虑到第三种变量的作用。
-
弱相关与强相关,相关系数越接近-1或+1,两个变量的线性关系就会越强,在0附近意味着两个变量没有货只有微弱的线性关系。存在强相关关系并不意味着变量之间存在因果关系,仅仅意味着有这种可能
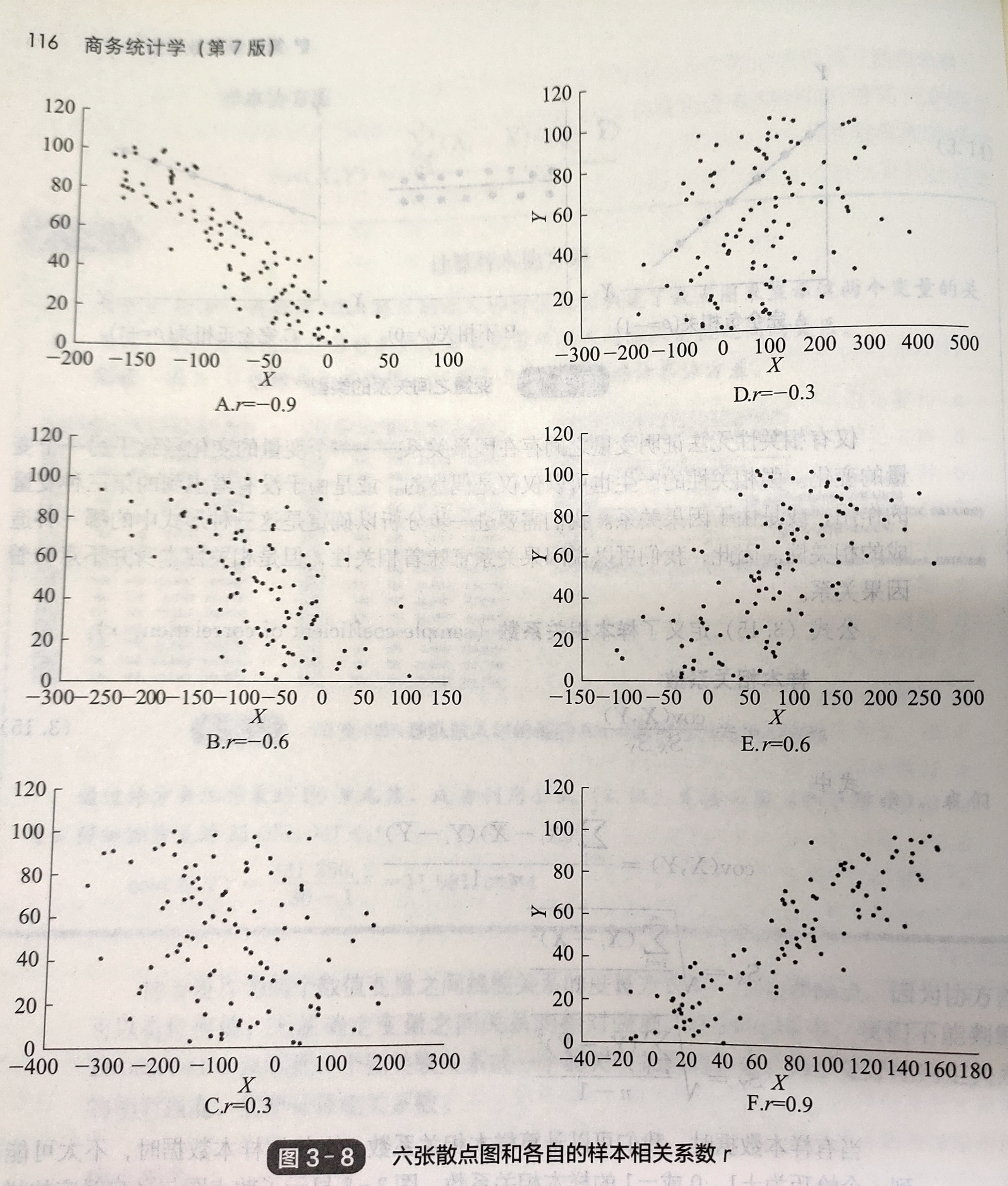
-
3.6 描述性统计量:缺陷和道德问题
- 在商务活动中,这些统计描述的方法进场包含在公司定期发布的总结性报告中
- 当决定报告结果是,在道德层面讲,好的画的结果都应该被记录,并且需要以一种公平、客观和中立的方式得结论
- 数据的描述性统计量应该综合起来看才能对数据有个更完善更准确的理解
- 比较均值和中位数,让你知道数据是对称的还是不对称的,中位数是不是比均值更好的展现数据集中趋势
- 对于非常偏的分布,留意标准差和四分位距是否包含在统计量中,没有他们将会很难判断这组数据有多大的变异程度。



