<sUbjeCt>Reverse aAlignment SemInaR

翻译过来就是有关逆序对问题的专题。

因为大胆报名担任学校专题讲师所以跪着也要准备好课件...那什么是逆序对？

逆序对就是序列中ai>aj且i<j的有序对

举个栗子：

5 4 2 6 3 1

其中，5>4，但是5的下标小于4，所以5 4是一对逆序对，同理还有：

5 4
5 2
5 3
5 1
4 2
4 3
4 1
2 1
6 3
6 1
3 1

共11对逆序对。

现在“愚蠢”的出题人让你求一下给定的数组[maxn]有几对逆序对，这就是经典的逆序对问题了。

 

题解一：归并排序

归并排序是上万种排序方法中的一种，复杂度为稳定的nlog(n)

应用的方法是分治的思想。

图片引自：https://www.cnblogs.com/chengxiao/p/6194356.html

 

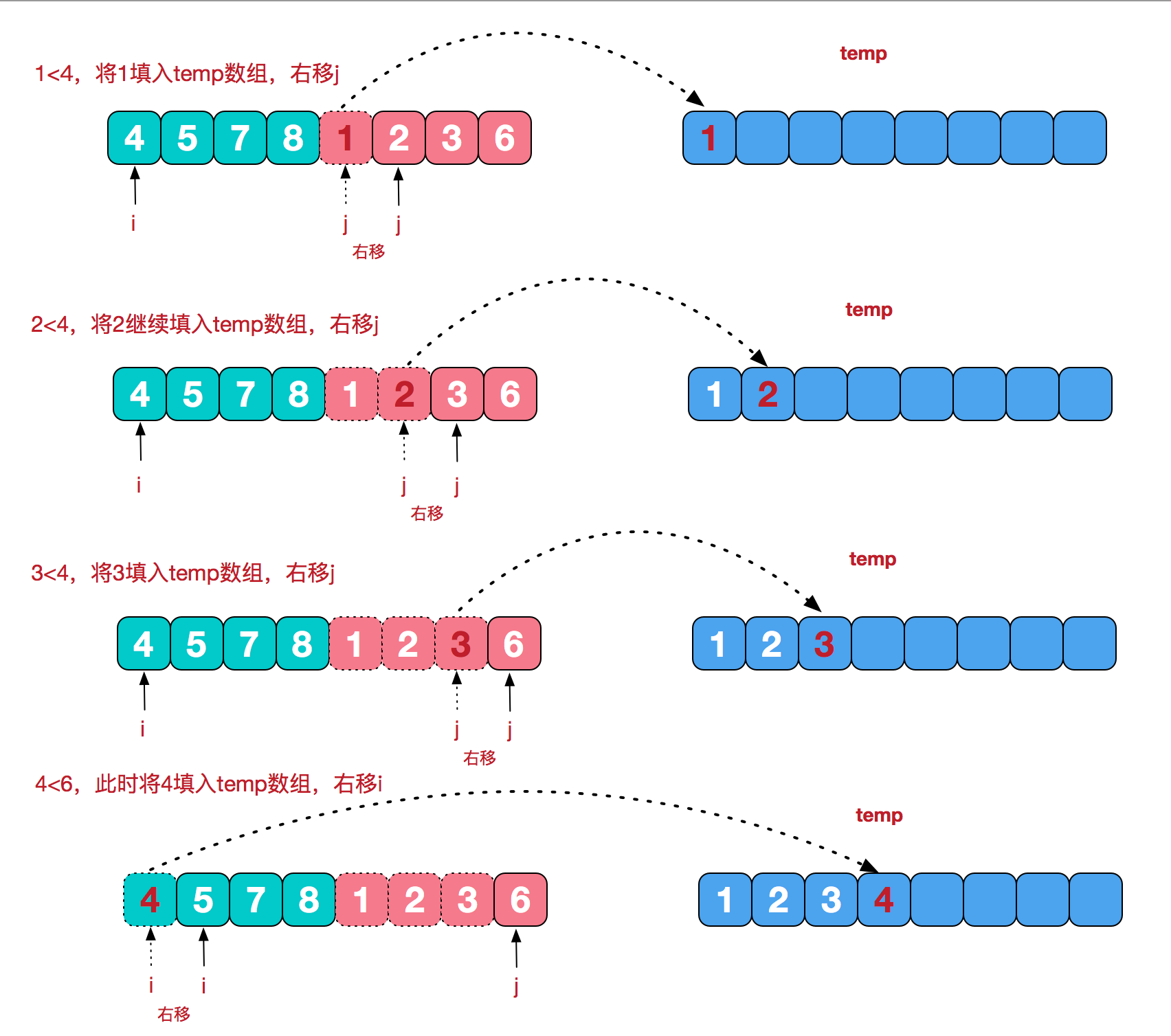
这就是千奇百怪的排序方式之一：归并排序的思路

#include<iostream>
using namespace std;
const int maxn=500000,INF=0x3f3f3f3f;
int L[maxn/2+2],R[maxn/2+2];
void merge(int a[],int n,int left,int mid,int right)
{
    int n1=mid-left,n2=right-mid;
    for(int i=0;i<n1;i++)
        L[i]=a[left+i];
    for(int i=0;i<n2;i++)
        R[i]=a[mid+i];
    L[n1]=R[n2]=INF;
    int i=0,j=0;
    for(int k=left;k<right;k++)
    {
        if(L[i]<=R[j])
            a[k]=L[i++];
        else
            a[k]=R[j++];
    }
}
void mergesort(int a[],int n,int left,int right)
{
    if(left+1<right)
    {
        int mid=(left+right)/2;
        mergesort(a,n,left,mid);
        mergesort(a,n,mid,right);
        merge(a,n,left,mid,right);
    }
}
int main()
{
    int a[maxn],n;
    cin>>n;
    for(int i=0;i<n;i++)
        cin>>a[i];
    mergesort(a,n,0,n);
    for(int i=0;i<n;i++)
    {
        if(i)
            cout<<" ";
        cout<<a[i];
    }
    cout<<endl;
    return 0;
} 

那这跟逆序对有什么关系呢。

其实归并排序只需要加一行代码就能代表逆序对数目

因为LA数组插入到A数组时，B数组剩下的所有都是符合逆序对标准的项

#include<stdio.h>
#include<string.h>
#define MAX 2100000000
int lef[300010],rig[300010];
int i,j,k,ans=0,n,a[500010]={0};
void merge(int left,int mid,int right){ 
    int n1=mid-left+1;
    int n2=right-mid;
    for(int i=1;i<=n1;i++){
        lef[i]=a[left+i-1];
    }
    for(int i=1;i<=n2;i++){
        rig[i]=a[mid+i];
    }
    lef[n1+1]=2100000000;
    rig[n2+1]=2100000000;
    int i=1,j=1;
    for(int k=left;k<=right;k++) 
    {
        if(lef[i]<=rig[j]){
            a[k]=lef[i++];  
        }else{
            ans+=n1-i+1;
            a[k]=rig[j++]; 
        }
    } 
    return ;
}
void merge_sort(int p,int r)
{//排序 
    if(p<r)//元素>1 
    {
        int mid=(p+r)/2;
        merge_sort(p,mid);
        merge_sort(mid+1,r);
        merge(p,mid,r);
    }
    return;
}
int main(void)
{
    scanf("%d",&n);
    for(i=1;i<=n;i++)
        scanf("%d",&a[i]);
    merge_sort(1,n);
    printf("%d",ans);
    return 0;
}

逆序对的朴素算法是从1开始到n-1结束，复杂度约为n*(n-1)/2，而归并排序是稳定的二分nlog（n）

题解二：Upper_Bound

什么是upper_bound？

upper_bound简单来说也是基于二分思想的查找，返回值是被查序列中第一个大于被查项的指针。

#include<cstdio>
#include<cstring>
#include<vector>
#include<algorithm>
using namespace std;
int n;
vector<int> shu;
int main(){
    scanf("%d",&n);    
    long long s=0,a;
    int kk[60000];
    for(int i=0;i<n;i++){
        scanf("%d",&kk[i]);//核心代码：
        s+=shu.end()-upper_bound(shu.begin(),shu.end(),kk[i]);
        shu.insert(upper_bound(shu.begin(),shu.end(),kk[i]),kk[i]);
    }
    printf("%d",s);
    return 0;
}