hdu 6129 Just do it

题

　　OvO http://acm.hdu.edu.cn/showproblem.php?pid=6129

　　（ 2017 Multi-University Training Contest - Team 7 - 1010）

解　　

　　假设初始数组s第一个为1，后面全是0，那么打出来的表为

　　

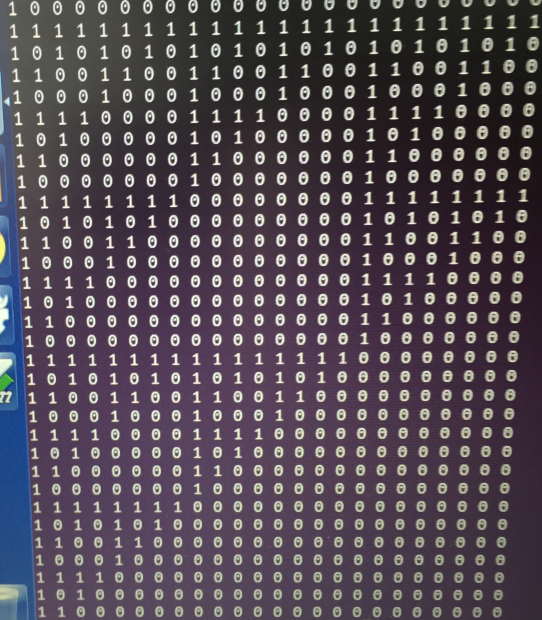
　　设原数组为s，第 2^k 次变换之后数组为p，显然s[i]只对p[i],p[i+2^k],p[i+2*2^k]……有贡献。

　　所以求m次变换之后的数组的话，对于m二进制中的第9位以上的1，进行跳跃（第i位跳跃2^i次)

　　然后剩下m小于2^10，直接暴力求

　　虽然比较慢，加个fread，过还是没什么问题的。

 

1981ms代码

#include <iostream>
#include <cstring>
#include <cmath>
#include <algorithm>
#include <cstdio>

using namespace std;
namespace fastIO {  
    #define BUF_SIZE 100000  
    //fread -> read  
    bool IOerror = 0;  
    inline char nc() {  
        static char buf[BUF_SIZE], *p1 = buf + BUF_SIZE, *pend = buf + BUF_SIZE;  
        if(p1 == pend) {  
            p1 = buf;  
            pend = buf + fread(buf, 1, BUF_SIZE, stdin);  
            if(pend == p1) {  
                IOerror = 1;  
                return -1;  
            }  
        }  
        return *p1++;  
    }  
    inline bool blank(char ch) {  
        return ch == ' ' || ch == '\n' || ch == '\r' || ch == '\t';  
    }  
    inline void read(int &x) {  
        char ch;  
        while(blank(ch = nc()));  
        if(IOerror)  
            return;  
        for(x = ch - '0'; (ch = nc()) >= '0' && ch <= '9'; x = x * 10 + ch - '0');  
    }  
    #undef BUF_SIZE  
};  
using namespace fastIO; 

const int M=2e5+44;

int s[2][M];
int n,m;
int ans[M];
int ansid;

void jmp(int k)
{
	ansid=1-ansid;
	memset(s[ansid],0,sizeof(s[ansid]));
	int i,j;
	
	for(i=1;i<=n;i++)
		for(j=0;i+j<=n;j+=k)
			s[ansid][i+j]^=s[1-ansid][i];
}

void solve(int m)
{
	ansid=0;
	int i,j;
	for(i=10;i<=30;i++)
		if(m&(1<<i))
		{
			m-=(1<<i);
			jmp(1<<i);
		}
	for(i=1;i<=m;i++)
	{
		ansid=1-ansid;
		s[ansid][0]=0;
		for(j=1;j<=n;j++)
			s[ansid][j]=s[ansid][j-1]^s[1-ansid][j];
	}
}

//inline void read(int &ret)
//{
//    int k=0;
//    char f=1;
//    char c=getchar();
//    for(;!isdigit(c);c=getchar() )
//        if(c=='-')
//            f=-1;
//    for(;isdigit(c);c=getchar() )
//        k=k*10+c-'0';
//    ret=k*f;
//}

int main()
{
//	freopen("test//fxxl1010.in","r",stdin);
// 	freopen("test//fxxl1010.out","w",stdout);
	int cas,i,j;
	read(cas);
	while(cas--)
	{
//		n=200000; m=((1<<30)-1);
//		for(i=1;i<=n;i++)
//			s[0][i]=rand()%(i+(1<<30));
		read(n); read(m);
		for(i=1;i<=n;i++)
			read(s[0][i]);
		solve(m);
		for(i=1;i<=n;i++)
		{
			if(i-1) printf(" ");
			printf("%d",s[ansid][i]);
		}
		printf("\n");
	}
	return 0;
}