【软工】个人项目作业——个人软件流程(PSP)
【软工】个人项目作业——个人软件流程(PSP)
| 项目 | 内容 |
|---|---|
| 班级:北航2020春软件工程 006班(罗杰、任健 周五) | 博客园班级博客 |
| 作业:设计程序求几何对象的交点集合 | 个人项目作业 |
| 个人课程目标 | 系统学习软件工程,训练软件开发能力 |
| 这个作业在哪个具体方面帮助我实现目标 | 实践个人软件开发流程(PSP) |
| 项目地址 | GitHub: clone/http |
个人软件流程(PSP)
| PSP2.1 | 预估耗时(分钟) | 实际耗时(分钟) |
|---|---|---|
| Planning | 20 | 20 |
| · Estimate | 20 | 20 |
| Development | 310 | 530 |
| · Analysis | 30 | 90 |
| · Design Spec | 10 | 30 |
| · Design Review | 10 | 10 |
| · Coding Standard | 10 | 10 |
| · Design | 40 | 90 |
| · Coding | 120 | 120 |
| · Code Review | 30 | 30 |
| · Test | 60 | 150 |
| Reporting | 50 | 50 |
| · Test Report | 20 | 20 |
| · Size Measurement | 10 | 10 |
| · Postmortem & Process Improvement Plan | 20 | 20 |
| In Total | 380 | 600 |
最终完成整个项目的时间远远超出了我的预计,其中与预期严重不符的项包括:分析需求、设计和测试。其中,分析需求和设计超时的原因是对题目要求功能的本质思考不清晰,思路和设计经过了以下的反复迭代和更改:
-
首先对参数在\((-10^5,10^5)\)范围时的交点取值范围进行了数学上的分析,认为线-线交点可能坐标高达\(4\times10^{10}\),精度要求可能高于\(10^{-5}\)。
-
于是认为使用
double维护点坐标精度不够,于是决定自行构造一个有理数类\(\frac{P}{Q}\),分子分母均为long long型 -
后来发现附加题里涉及到圆,线-圆交点的形式为\(\frac{A+B\sqrt{C}}{D}\),于是决定扩展有理数类到支持带系数的根式。再思考如何标准化该式以进行两坐标之间的比较(哈希和判等),涉及到了质因数分解等。
-
再仔细分析,认为线-线交点范围可能达到\(4\times 10^{10}\),再由于double类型的有效数字仅为15位左右,即小数点后5位左右,因此认为应当使用有理数类存储线线交点以避免精度问题。然而对线-圆交点和圆-圆交点而言,交点范围必在\(\pm 2\times 10^{5}\)以内,因此使用double存储可到小数点后近10位,因此涉及到圆的交点可以使用double,精度足够。在比较时认为有理数≠double小数。
-
又发现线线交点可能和圆交点重合,于是必须检查涉及到圆的交点坐标是否为有理数。是有理数则使用有理数类,否则使用double。这要求将坐标的公式写出,检查根号内的整数是否为完全平方数。若是完全平方数则可以化为有理数类,否则直接求值。
可以看出,如果一开始就较为清晰地将各个需求罗列出来,再一一分析,分析之后再进行统一设计,可能很快就可以想出有理数/无理数的分类,而不是将所谓设计的有理数类反复拓展以支持新需求。
如果是一边像这样设计一边写代码,浪费的时间就更是灾难性的,代码将会反复修改,思路也会频繁被打断。
因此PSP看似麻烦复杂的流程不是没有道理的,以后应当记住这个教训。
解题思路
此题使用哈希表的暴力解法时间复杂度为\(O(n^2)\)。容易考虑到有两种优化条件,分别为 “平行线” 和 “多线共点”。对于前者可以按斜率进行等价类划分,在类间进行两两求交;对于后者需要额外计算判断是否共点,也会带来常数的提升。
因此笔者仍然选择暴力解法,枚举每pair的几何对象组合,计算交点,使用哈希集合维护去重。
点的维护
三种交点有着三种不同的公式。首先将它们的通式推导出来。具体的推导和公式可以参照:
- 线-线交点: Wikipedia
- 线-圆交点: Wolfram MathWorld
- 圆-圆交点: Stack Overflow
其中,线线交点可以写成如下形式:
其中\(x_1,x_2,y_1,y_2\)均为整数表达式的运算结果。于是,设计一个有理数类存储线-线交点的坐标(不使用double的理由见上节)以便于哈希和比较。
然而,线-圆交点和圆-圆交点的形式为:
其中\(x_\bullet,y_\bullet, \Delta\)均为整数表达式的运算结果。当\(\Delta\)为完全平方数时,该式化简为有理数形式;否则,该式为无理数。
考虑到有理数不可能等于无理数,因此首先检查\(\Delta\)是否能开根,若可以则使用有理数类,否则直接求值使用double存储(此处可以使用double的理由见上节)。
求交点:四种二元关系
假设有类Line和类Circle存储两类几何对象。然而求交点需要(Line, Line), (Line, Circle), (Circle, Line), (Circle, Circle)四种组合。
一开始,我倾向于使用父类和子类维护不同的几何对象,但发现即使使用重载和重写,代码效率和可读性并没有明显的提高。
后来通过查找资料,我在 这篇问答帖子 中找到了最佳的解决方案:使用std::variant和std::visit来优美地实现“多态二元函数”。
std::variant相当于一种升级版的union类型,可以安全地存储不同类型的对象,可以通过index()方法取得某对象的类型,也可以通过std::get<type>(x)取得variant对象x的值。不仅如此,它还支持使用std::visit(visitor, vars)去自动处理各种类型为参数的函数调用(可以参考cppReference.com),正好和该问题的需求相匹配!其中,visitor是一个封装了callable函数的结构体,能支持每个参数的每种类型组合,vars是待传入的variant参数列表。
具体实现请见“代码说明”。
交点集合的维护(去重)
C++中的set基于BST实现,在此我们并不需要对点进行排序和有序组织,因此考虑使用unordered_set来维护点,相当于Java中的HashSet。要使用unordered_set,必须提供哈希函数和判等函数。
对于点来说,有x和y两个坐标,在哈希时只需将两个坐标获取哈希值再进行组合即可,在判等时需要注意先验条件“有理数不等于无理数”以保证正确性!
而坐标有整数数对(有理数)和浮点数(double)两种形式,在判等时应当注意判断等号两端坐标分别点类型。
注意到在哈希和判等前,坐标必须进行化简(\(\frac{8}{6}=\frac{4}{3}\))和标准化(\(\frac{-0}{8}=\frac{0}{1}\)),因此使用辗转相除法求最大公约数,再消去该因子。
由于这里分子和分母有可能较大,因此普通的辗转相除法可能效率较低。一个优化的辗转相除法可以参照《编程之美》2.7节《最大公约数问题》。该算法检查两数的奇偶性,当至少有一个数为偶数的情况下,数值的规模将会直接减半。当两个数为奇数时,算法避免了较慢的除法和取模运算,而是使用辗转相减,使得再次出现偶数。因此,该算法的最坏时间复杂度为\(O(\log_2(\max(x,y))\),十分理想。
具体实现请见“代码说明”。
设计
类与数据结构
如上文所说,基础的数据结构是坐标,支持两种形式的数,构造时化简和标准化。支持hashCode。
class Coordinate {
// Case 1: Rational Number = A / B (long-long / long-long)
// Case 2: Float Number = C (double)
private:
void simplifyRational();
void simplifySqrt(ll add, ll coeff, ll insqrt, ll btm);
public:
bool isRational, isNan;
ll top, bottom;
double value;
Coordinate(ll tp, ll btm); // tp / btm
Coordinate(ll a, ll b, ll c, ll btm); // ( a + b * sqrt(c) ) / btm -----> (1) A / B or (2) double value
std::size_t hashCode() const ;
};
坐标组成点,点可以求哈希值和判等:
class Point {
public:
Coordinate x, y;
Point(Coordinate xx, Coordinate yy);
};
struct hashCode_Point {
std::size_t operator()(const Point &point) const ;
};
struct equals_Point {
bool operator()(const Point &lhs, const Point &rhs) const ;
};
几何对象有直线和点,它们之间支持两两求交点:
class Line {
public:
Line(int x1, int y1, int x2, int y2);
int p1_x, p1_y;
int p2_x, p2_y;
};
class Circle {
public:
Circle(int x, int y, int r);
int center_x, center_y;
int radius;
};
std::vector<Point> intersection(Line x, Circle y);
std::vector<Point> intersection(Circle x, Line y);
std::vector<Point> intersection(Line x, Line y);
std::vector<Point> intersection(Circle x, Circle y);
最后使用基于哈希的unordered_map维护点集:
std::unordered_set<Point, hashCode_Point, equals_Point> container;
代码说明
坐标与交点
优化的最大公约数算法,为化简作准备:
ll fastGcd(ll x, ll y) {
if (x < y)
return fastGcd(y, x);
if (!y)
return x;
// 使用位运算以避免较慢的除法和取模
if ((x >> 1u) << 1u == x) {
// 两个偶数 或 一奇一偶
if ((y >> 1u) << 1u == y) return (fastGcd(x >> 1u, y >> 1u) << 1u);
else return fastGcd(x >> 1u, y);
} else {
// 一奇一偶 或 两个奇数
if ((y >> 1u) << 1u == y) return fastGcd(x, y >> 1u);
else return fastGcd(y, x - y);
}
}
标准化有理数,检查是否能开根号将“无理数”化为有理数:
void Coordinate::simplifyRational() {
// 化简成分母为正数、分子符号不定的最简分数
assert(isRational);
// now bottom != 0
// 6 / -4 --> -3 / 2
if (bottom < 0) {
top = -top;
bottom = -bottom;
}
// now bottom > 0 ---> gcd != 0
ll gcd = fastGcd(abs(bottom), abs(top));
top /= gcd;
bottom /= gcd;
}
void Coordinate::simplifySqrt(ll add, ll coeff, ll insqrt, ll btm) {
// 检查是否可开根号成有理数
ll tryRoot = sqrt(insqrt);
if (tryRoot * tryRoot == insqrt) { // actually a RATIONAL !
isRational = true;
top = add + coeff * tryRoot;
bottom = btm;
simplifyRational();
}
}
坐标数值的哈希函数与点的哈希函数:
std::size_t Coordinate::hashCode() const {
if (isRational) {
std::size_t h1 = std::hash<long long>{}(top);
std::size_t h2 = std::hash<long long>{}(bottom);
// 参考标准库的写法,将两子成员的哈希值合并
return ((h1 ^ (h2 << 1u)) << 1u) | 1u;
} else {
std::size_t h = std::hash<double>{}(value);
// 有先验知识:有理数≠无理数
// 有理数的哈希值末尾为1,无理数的哈希值末尾为0
return (h << 1u) | 0u;
}
}
struct hashCode_Point {
std::size_t operator()(const Point &point) const {
std::size_t h1 = point.x.hashCode();
std::size_t h2 = point.y.hashCode();
// 参考标准库的写法,将两子成员的哈希值合并
return h1 ^ (h2 << 1u);
}
};
点的判等函数:
struct equals_Point {
bool operator()(const Point &lhs, const Point &rhs) const {
// 按成员比较。注意有先验知识:有理数≠无理数
bool x_eq = false, y_eq = false;
if (lhs.x.isRational) {
x_eq = (rhs.x.isRational & (lhs.x.top == rhs.x.top) & (lhs.x.bottom == rhs.x.bottom));
} else {
// 无理数取小数点八位进行比较
x_eq = ((!rhs.x.isRational) & ((long long)(lhs.x.value * 1e8) == (long long)(rhs.x.value * 1e8)));
}
if (lhs.y.isRational) {
y_eq = (rhs.y.isRational & (lhs.y.top == rhs.y.top) & (lhs.y.bottom == rhs.y.bottom));
} else {
y_eq = ((!rhs.y.isRational) & ((long long)(lhs.y.value * 1e8) == (long long)(rhs.y.value * 1e8)));
}
return x_eq & y_eq;
}
};
直线与圆求交点
两两求交点,共四种组合的自动匹配:
// 使用 std::variant 和 std::visit 来实现“多态二元函数” !
// 重载四种组合
std::vector<Point> intersection(Line x, Circle y);
std::vector<Point> intersection(Circle x, Line y);
std::vector<Point> intersection(Line x, Line y);
std::vector<Point> intersection(Circle x, Circle y);
// 类型的定义,相当于 union
using Geometry = std::variant<Line, Circle>;
// 重载()运算符以实现类型匹配
struct interset_visitor {
template<typename Shape1, typename Shape2>
std::vector<Point> operator()(const Shape1 &lhs, const Shape2 &rhs) const {
return intersection(lhs, rhs);
}
};
// 定义hashSet,传入哈希函数和判等函数
std::unordered_set<Point, hashCode_Point, equals_Point> container;
for (int i = 0; i < objCount; ++i) {
for (int j = i + 1; j < objCount; ++j) {
// 使用 std::visit 重定向四种重载的参数组合
std::vector<Point> intersections = std::visit(interset_visitor{}, (*objs)[i], (*objs)[j]);
for (Point p: intersections)
container.insert(p);
}
}
单元测试
为使程序跨平台且具有较好的可拓展性,笔者没有采用VS自带的单元测试框架,而是使用了其支持的 GoogleTest。
笔者针对坐标&点、几何&求交这两个主要功能和数据单元进行了数十项单元测试,测试点主要功能点如下所示:
- 坐标和点的构造与化简 GoogleTest Code
- 有理数的构造
- 无理数的构造和求浮点值
- 有理数的化简
- 复杂式化简成有理数
- 复杂式无法化简成有理数
- 分子分母各个位置上的负数、0、正数、极小值、极大值
- 非法坐标(交点在无穷远)
- 随机参数对象
- 两个几何对象求交点 GoogleTest Code
- 平行于坐标轴的直线
- 非平凡的直线
- 交点为有理数的直线
- 交点为有理数的线-圆和圆-圆
- 交点为无理数的线-圆和圆-圆
- 线-圆相交、相切、相离
- 圆-圆相交、内外切、内外离
- 随机参数对象
运行结果为:


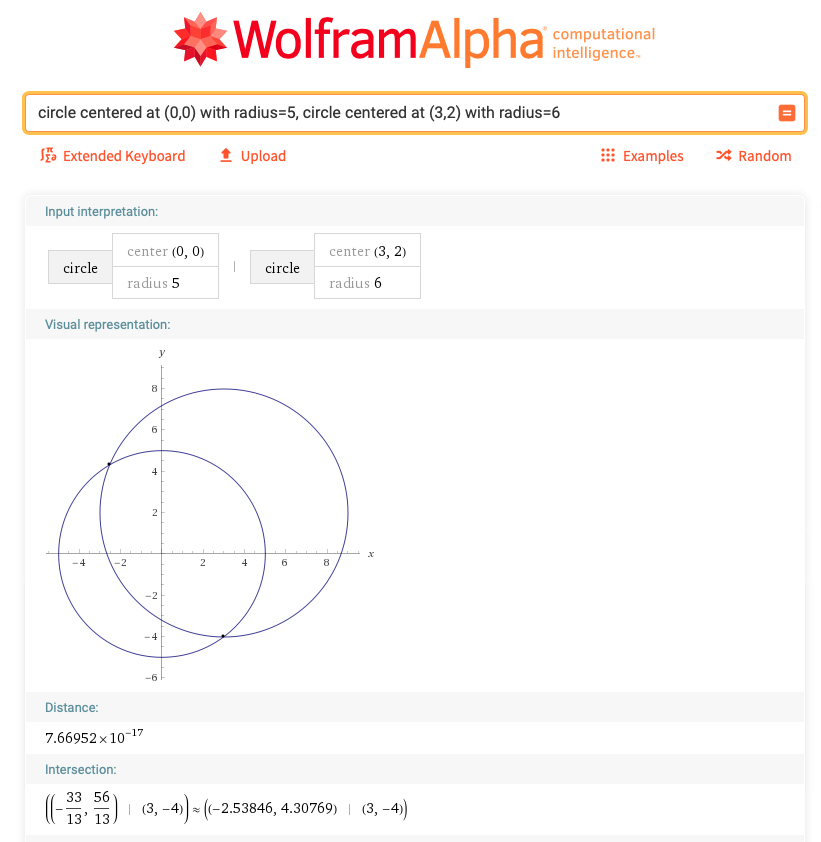
笔者使用Wolfram Alpha来辅助调试和获取正确答案:
性能改进
笔者使用VS 2019 Community进行了效能分析测试,第一次测试结果如下:
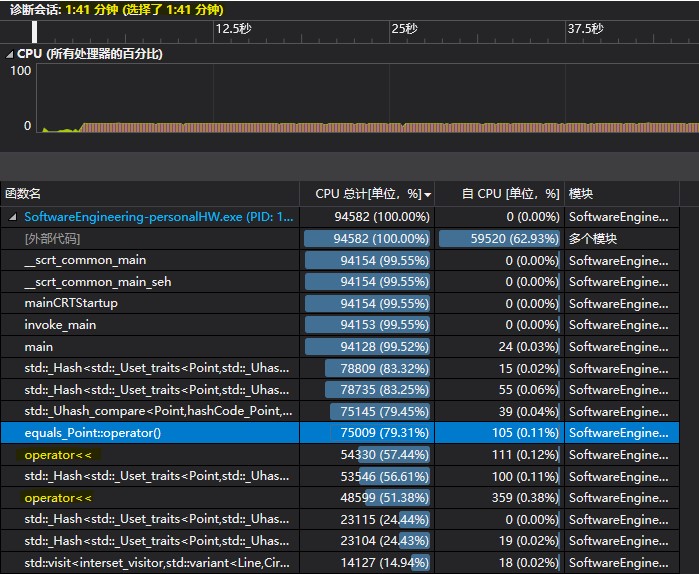
可以看到,operator <<占了很多的时间,导致判等函数占用很多时间,同时程序运行超时。
这是因为为了简单起见,在哈希表的判等中,笔者使用单元测试时验证过的输出函数将对象转换成字符串,再进行字符串的比较。这样时间主要浪费在了构造字符流、构造字符串和比较字符串上。
因此,笔者对其进行了改进,将使用输出到字符串再比较替换成了按逻辑比较成员变量:
struct equals_Point {
bool operator()(const Point &lhs, const Point &rhs) const {
/* TIME-COSTING !!!
std::ostringstream outstream1, outstream2;
outstream1 << lhs;
outstream2 << rhs;
return outstream1.str() == outstream2.str();
*/
bool x_eq = false, y_eq = false;
if (lhs.x.isRational)
x_eq = ...;
else
x_eq = ...;
if (lhs.y.isRational) ...
return x_eq & y_eq;
}
};
第二次测试的结果如下:
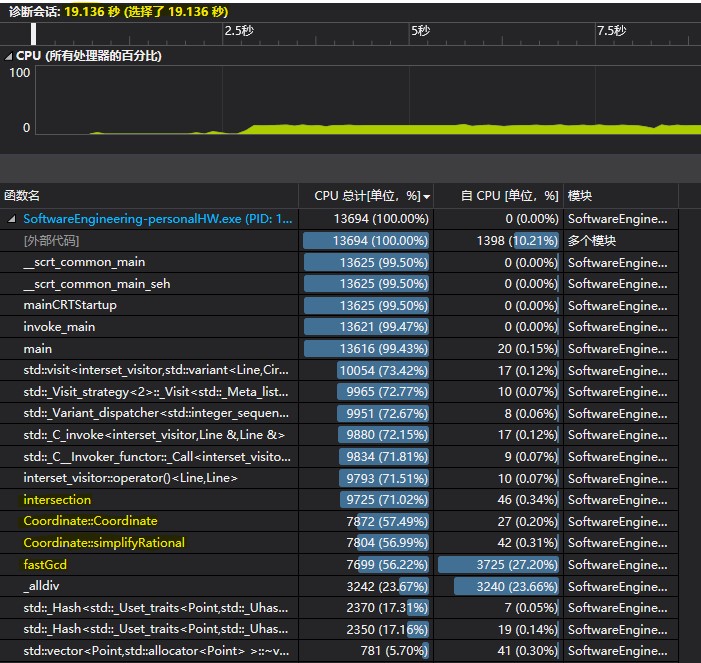
可以看出,现在程序的主要运行时间花费分布十分合理,主要在求交点、构造交点、化简交点、求最大公约数这一条调用链上。程序的运行时间也从100s缩短到了19s。
代码风格与质量
笔者使用VS 2019 Community进行了代码质量分析(Microsoft建议的分析),改正代码后的结果如下:

其中关于freopen和scanf的警告,在此次作业确保调用方式正确、输入数据正确的情况下,笔者为了效率和性能,没有将其替换成freopen_s、scanf_s等,也没有增加相应的代码处理它们的返回值。
最后一条警告的对象是下面一条语句:
ll insideSqrt;
...
ll possibleRoot = sqrt(insideSqrt);
工具警告我们将double转成long long可能丢失数据,但我们明确知道sqrt()内部的值是long long型的整数,且取值范围在\(\pm4\times 10^{10}\)内,开根号后取值范围必定不会变大到与double的取值范围相当,因此笔者明确知道此处的写法是安全的且符合程序员本意的,因此有意忽略。



