2016012015+小学四则运算练习软件项目报告
1.仓库地址:https://git.coding.net/FrrLolix/Calculate.git
2.需求分析:
①程序接受一个输入的参数n后,随机生成n道四则运算式,其中要保证生成的运算式的运算符在3-5个之间,同时程序对生成的运算式自动求解,结果和运算式一同输出到result.txt文件中。
②因为面向对象是小学生,所以要保证生成的运算式中不出现负数和小数,运算的结果也不能出现负数和小数。
③程序需要判断输入的参数n是否合法,在不合法时要进行一定的处理。
④在原有的基础上,生成的运算式随机性的带有括号和真分数。
3.功能设计:
①基本功能:
Ⅰ程序接收参数n,并对n的合法性作出判断,若出现错误则提示。
Ⅱ自动生成n个运算式,并计算得出结果。
Ⅲ将计算后的结果与运算式一同存入txt文件中,保存在指定目录下。
②扩展功能:
Ⅰ由于面向对象是小学生,因此数字在0-100之间。
Ⅱ随机产生括号并保证括号的合法有效性。
Ⅲ加入分数运算式,并且保证计算前后都是真分数,且不可化简。
4.设计实现:
①整体思路:
Ⅰ四则运算:首先产生5个随机数和一个flag作为标志,flag的值为随机0-3,分别代表了不同数量的运算符和分数运算,确定了flag的值后,产生随机的运算符将数字连接,构成运算式,再将运算符和数字拆分,利用两个栈分别放置,将原本的运算式转化成后缀表达式,从而进行计算,这也是逆波兰表达式的计算方法。
Ⅱ带括号计算:以3个运算符的计算为例,括号只能存在于前两个数字和后两个数字中,因此设置location这一参数,location为0时,括号在前,location为1时括号在后,分别进行讨论,确定括号的位置,生成带括号的运算式,在后续计算过程中,注意要增加括号的入栈和出栈操作。
Ⅲ真分数的计算:对于真分数,首先随机产生0-100的某个数,然后随机产生一个比刚刚生成的数小的数,通过辗转相除法,生成真分数并输出。
对于整体而言,我只使用了一个类,通过这个类来调用不同的方法解决问题。
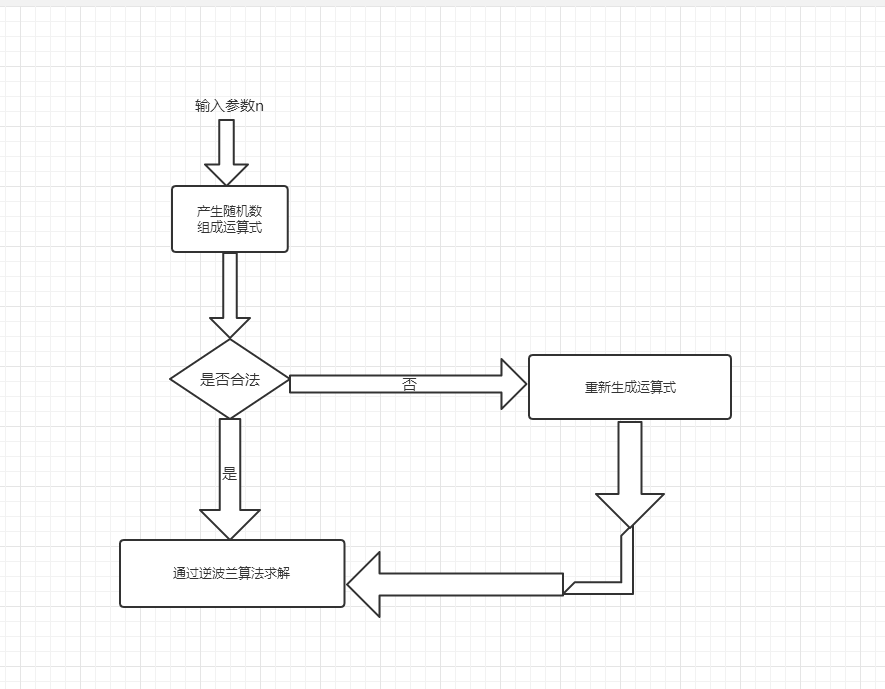
②设计的函数:
Ⅰ构成3个运算数的运算式的方法: three(int n1,int n2,int n3)
Ⅱ构成4个运算数的运算式的方法:four(int n1,int n2,int n3,int n4)
Ⅲ构成5个运算数的运算式的方法:five(int n1,int n2,int n3,int n4,int n5)
Ⅳ实现计算的方法:Calculate(String s)
Ⅴ分式化简的方法:gcd(int a,int b)
5.代码详情:
①生成表达式的算法:
Ⅰ这里使用一个循环,flag用于判断每次循环产生的结果,根据flag的不同调用不同的方法
for(i=0;i<n;i++){ int n1=ran.nextInt(100);//生成一个0-100的整数 int n2=ran.nextInt(100); int n3=ran.nextInt(100); int n4=ran.nextInt(100); int n5=ran.nextInt(100); int flag=ran.nextInt(4);//随机生成一个0-3的整数,0表示3个运算数,1表示4个运算数,2表示5个运算数,3表示分数计算
Ⅱ此处是flag=3时,分数的生成方法
n1=1+ran.nextInt(101); n2=1+ran.nextInt(101); n3=1+ran.nextInt(101); int M,Z; int x1,x2,x3; x1=1+ran.nextInt(n1);//生成一个比分母n1小的分子,实现真分数 x2=1+ran.nextInt(n2);//生成一个比分母n2小的分子,实现真分数 x3=1+ran.nextInt(n3);//生成一个比分母n3小的分子,实现真分数 Z=x1*n2*n3+x2*n1*n3+x3*n1*n2; M=n1*n2*n3; String d=gcd(Z,M); s=x1+"/"+n1+"+"+x2+"/"+n2+"+"+x3+"/"+n3+"="+d; pw.write(s+"\r\n"); // \r\n即为换行
Ⅲ此处是3个运算符是运算式的生成方法,我在这里进行了讨论,加入了是否有括号的两种情况,对于括号的位置进行设定,随后输出不同的结果,此处代码较长,只展示一部分,详细的可以在Coding.net上查询
String s1= new String(); Random ran = new Random(); int sign1=ran.nextInt(4);//随机生成一个0-3的整数,0表示加法,1表示减法,2表示乘法,3表示除法 int sign2=ran.nextInt(4); int sign3=ran.nextInt(2);//如果是1表示有括号,如果是0 表示无括号 int sign4=ran.nextInt(2);//如果是1表示产生分式,如果是0 表示整式。 if(sign1==sign2) { sign2=(sign1+1)%3;//保证两个运算符不相同。 } if(sign3==0)//表示无括号 { //下面的过程为排除,除不整的,还有分母为0, if(sign2==3) { if(n3==0)//如果分母为0 n3=1+ran.nextInt(100);//随机生成一个1-100的整数 while(n2%n3!=0) { n2=ran.nextInt(100); } }
②计算方法
Ⅰ计算方法我采用了逆波兰表达式的算法,这一部分是之前困扰我最久的地方,起初想了许多方法来尝试,但都有些繁琐,实施起来并不是很容易,因此我也在其他博客上参考学习了许多,最终选定了逆波兰表达式,逆波兰表达式的思路为
1.遇到操作数:直接输出(添加到后缀表达式中)
2.栈为空时,遇到运算符,直接入栈
3.遇到左括号:将其入栈
4.遇到右括号:执行出栈操作,并将出栈的元素输出,直到弹出栈的是左括号,左括号不输出。
5.遇到其他运算符:加减乘除:弹出所有优先级大于或者等于该运算符的栈顶元素,然后将该运算符入栈
6.最终将栈中的元素依次出栈,输出。
下面截取了遇到等号时的代码处理。
case '(': { stack2.push(String.valueOf(c));//如果是( 转化为字符串压入字符栈 break; } case ')': {//遇到右括号了计算,因为(的优先级最高 String stmp = stack2.pop();//如果是),将符号栈栈顶元素取到 while (!stack2.isEmpty() && !stmp.equals("(")) { //当前符号栈里面还有+ - * / int a = stack1.pop(); //取操做数a,b int b = stack1.pop(); int sresulat = calculate(b, a, stmp); if(sresulat<0) return -1; stack1.push(sresulat);//将结果压入栈 stmp = stack2.pop();//符号指向下一个计算符号 } break; }
6.测试运行:
进入src文件下,输入javac -encoding utf-8 Main.java 编译出相应的class文件,再输入java Main 进行测试:
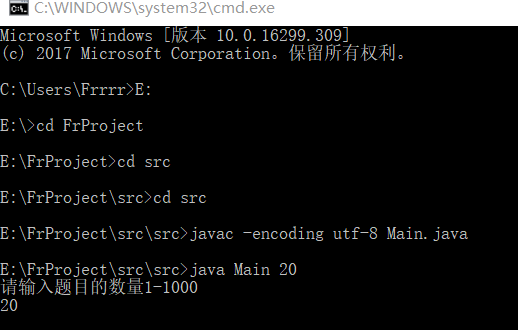
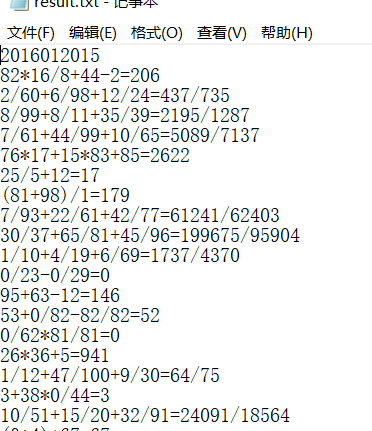
7.不足与改进:
在算法的实现过程中,虽然经过了不断的修改和调整,但目前仍然存在着许多不足:
1.括号的处理,只是处理了几种特殊情况,并没有做到括号的随机并合理,没有涉及到多重括号的生成和处理,这也是以后改进的一个方向。
2.在出题的过程中,我的方法是将不同数量的运算符的算法之间分离开,造成算法的延展性较差,目前也参考了同学们的代码,发现自己的代码如果扩展到10个运算符的情况,会很麻烦,这是接下来需要改进的一点。
3.在最开始进行算法的分析的时候,没有注意题目的要求,也没有看到老师推荐的调度场算法,因此,在计算上大费周章,这是今后要避免的一个问题,对于项目要求一定要认真理解。
8.项目总结:
1.在算法的编写过程中,采用了书中和老师所推荐的“逐步求精”的设法方法,将一个项目分解成几个不同的小问题,通过编写不同的方法来逐步解决每个问题,各个方法相互配合,循序渐进,最终达成自己想要的结果。
2.对于算法编写中出现的许多问题,进行了思考和改进,并且对于项目的延展性有了更深的理解,我的算法延展性不强,这是以后和强化的一点。
9.PSP展示
|
PSP2.1 |
任务内容 |
计划共完成需要的时间(min) |
实际完成需要的时间(min) |
|
Planning |
计划 |
8 |
10 |
|
· Estimate |
· 估计这个任务需要多少时间,并规划大致工作步骤 |
8 |
6 |
|
Development |
开发 |
600 |
1200 |
|
· Analysis |
· 需求分析 (包括学习新技术) |
20 |
30 |
|
· Design Spec |
· 生成设计文档 |
10 |
10 |
|
· Design Review |
· 设计复审 (和同事审核设计文档) |
5 |
5 |
|
· Coding Standard |
· 代码规范 (为目前的开发制定合适的规范) |
3 |
5 |
|
· Design |
· 具体设计 |
10 |
20 |
|
· Coding |
· 具体编码 |
500 |
950 |
|
· Code Review |
· 代码复审 |
10 |
20 |
|
· Test |
· 测试(自我测试,修改代码,提交修改) |
15 |
30 |
|
Reporting |
报告 |
10 |
30 |
|
· Test Report |
· 测试报告 |
5 |
10 |
|
· Size Measurement |
· 计算工作量 |
1 |
1 |
|
· Postmortem & Process Improvement Plan |
· 事后总结, 并提出过程改进计划 |
5 |
15 |




