【USACO 2021JAN P】Minimum Cost Paths

【USACO 2021JAN P】Minimum Cost Paths

by AmanoKumiko

Description

平面直角坐标系中（其实是给出\(N*M\)的方阵）

点\((x,y)\)可以用\(x^2\)的代价使\(y+1\)，可以用\(c_y\)的代价使\(x+1\)

给出\(Q\)组询问

每次求出\((1,1)\)到\((xi,yi)\)所需的最小代价

Input

第一行\(N\)，\(M\)

第二行\(M\)个数\(c_1,c_2...c_m\)

第三行\(Q\)

最后\(Q\)行为询问

Output

\(Q\)行，表示答案

Sample Input

5 4
1 100 100 20
20
1 1
2 1
3 1
4 1
5 1
1 2
2 2
3 2
4 2
5 2
1 3
2 3
3 3
4 3
5 3
1 4
2 4
3 4
4 4
5 4

Sample Output

0
1
2
3
4
1
5
11
19
29
2
9
20
35
54
3
13
29
49
69

Data Constraint

\(2 \le N \le 10^9\)，\(2 \le M,Q \le 2·10^5\)

Solution

对于每个询问，可以发现答案的路径是一条折线，考虑维护

离线，按\(y\)排序

我们记录折线上的所有拐点(即图中的红点)

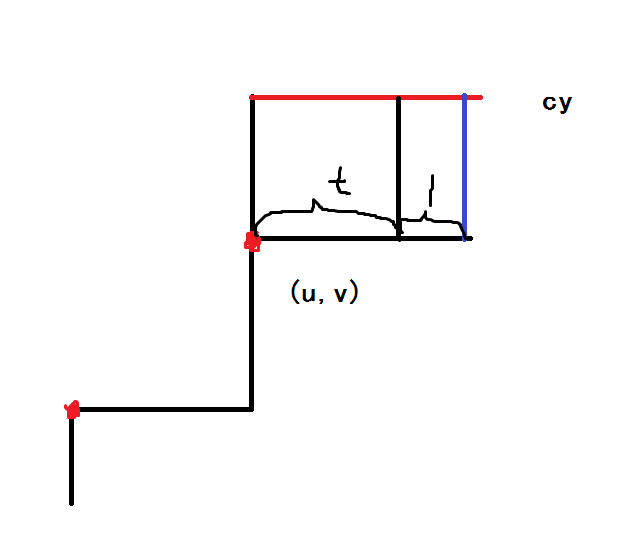
对于新加入的\(c_y\)

设当前拐点为\((u,v)\)

若\(c_y\)优于\(c_v\)

考虑从\((u,v)\)往上走

则有\((y-v)·u^2+c_y·t<(y-v)(u+t)^2+c_v·t\)

化简得\(\frac{c_y-c_v}{y-v}<2u+t\)

那么当\(\frac{c_y-c_v}{y-v}<2u\)时，\(c_y优于c_v\)，删除\(c_v\)

否则，考虑找出新的拐点

若从紫色路径往上劣于走它左边的黑色路径

则\(c_v·t+(u+t)^2(y-v)+c_y<c_v·(t+1)+(u+t+1)^2(y-v)\)

化简得\(\frac{c_y-c_v}{y-v}<2(u+t)+1\)

移项算出最小的\(t\)，于是得到新拐点\((u+t,y)\)

维护拐点的同时，算出到每个拐点的答案（前缀和）

对于询问，二分找到最近的拐点即可

Code

#include<bits/stdc++.h>
using namespace std;
#define F(i,a,b) for(int i=a;i<=b;i++)
#define Fd(i,a,b) for(int i=a;i>=b;i--)
#define Ld long double
#define LL long long
#define N 200010

LL c[N],ans[N],sum[N];
struct node{LL x,y;int pos;}ask[N];
struct point{LL x,y;}tr[N];
int n,m,q,h,l,r,mid,top;

Ld Slope(LL x,LL y){return 1.0*(c[x]-c[y])/(x-y);}

bool cmp(node a,node b){return a.y<b.y||a.y==b.y&&a.x<b.x;}

LL cost(point a,point b){return (b.x-a.x)*c[a.y]+(b.y-a.y)*b.x*b.x;}

void insert(LL p){
	while(Slope(p,tr[top].y)<2.0*tr[top].x)top--;
	LL w=ceil((Slope(p,tr[top].y)-1.0)/2.0+0.000001);
	top++;
	tr[top]=(point){top==1?1:w,p};
	sum[top]=sum[top-1]+cost(tr[top-1],tr[top])-(top==1);
}

int main(){
	scanf("%d%d",&n,&m);
	F(i,1,m)scanf("%lld",&c[i]);
	scanf("%d",&q);
	F(i,1,q)scanf("%lld%lld",&ask[i].x,&ask[i].y),ask[i].pos=i;
	sort(ask+1,ask+q+1,cmp);
	tr[top=h=1]=(point){1,1};
	F(i,1,q){
		while(h+1<=ask[i].y)insert(++h);
		l=0;r=top+1;
		while(l<r-1)mid=l+r>>1,tr[mid].x>ask[i].x?r=mid:l=mid;
		ans[ask[i].pos]=sum[r-1]+cost(tr[r-1],(point){ask[i].x,ask[i].y});
	}
	F(i,1,q)printf("%lld\n",ans[i]);
	return 0;
}