树形DP学习笔记
昨天b组第三题正解树形DP加tarjan求环;但我一个都不会。。。。。。
趁8.8放假,学习一波:
1.存树{
存树还是不太熟悉,邻接矩阵,邻接表,双亲,孩子;
我还是喜欢用邻接矩阵,好理解,再加双亲找根。
(后加)做了几题后发现用孩子表示法也挺方便的XD}
2.dfs{
dp转移要么从子到父,要么从父到子,
在dfs时dp方程位置要注意
子到父应在dfs之后回溯时更新;
父到子应在dfs之前更新。
}
分析:对于每一个节点,只有取和不取两种状态,根节点取了子节点一定不取,
但根节点不取子节点可取也可不取;
则根节点处最优值应该把它子节点最优值累加
方程如下:
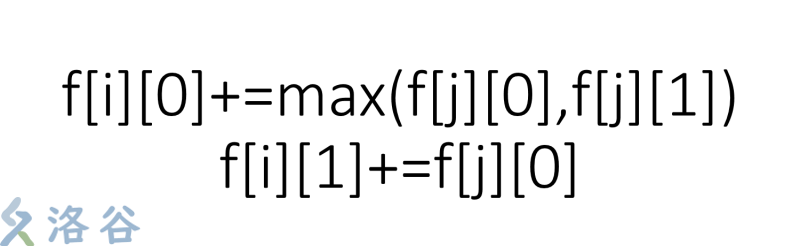
其中i为根节点,j为子节点,0表示不取这个点,1表示取;
最后答案就只需要比较一下树顶取和不取取最大值就好啦;
代码如下

#include<iostream> #include<cstdio> using namespace std; int parent[7000],happy[7000],n,f[7000][2]; bool child[6100][6100]; inline int read() { int f=1,x=0;char c=getchar(); while(c<'0'||c>'9'){if(c=='-')f=-1;c=getchar();} while(c>='0'&&c<='9'){x=(x<<3)+(x<<1)+(c^48);c=getchar();} return f*x; } int max(int x,int y){return x>y?x:y;} void dfs(int x) { f[x][1]=happy[x];f[x][0]=0; for(int i=1;i<=n;i++) { if(child[x][i]) { dfs(i); f[x][1]+=f[i][0]; f[x][0]+=max(f[i][0],f[i][1]); } } } int main() { n=read(); for(int i=1;i<=n;i++)happy[i]=read(); for(int i=1;i<=n;i++) { int a,b; a=read();b=read(); if(!a&&!b)break; parent[a]=b; child[b][a]=1; } int geng=1; while(parent[geng])geng++; dfs(geng); int ans=max(f[geng][0],f[geng][1]); cout<<ans; return 0; } P2015 二叉苹果树 就像蓝书中说的一样,对于q根树枝,要选q+1个节点,根节点最优值转移方程如下图: j-k-1是因为要把根节点也算上,这样k+j-k-1+1=j; f[i][j]表示的是在i号节点为根节点的树中取j个节点能取得的最优值; 那么题目中给的苹果在边上怎么办? 书中也给了解决办法,把边权下移到点中就行啦。 代码如下 #include<iostream> #include<cstdio> using namespace std; int n,q,f[110][110],mp[110][110],a[110],l[110],r[110]; inline int read() { int f=1,x=0;char c=getchar(); while(c<'0'||c>'9'){if(c=='-')f=-1;c=getchar();} while(c>='0'&&c<='9'){x=(x<<3)+(x<<1)+(c^48);c=getchar();} return f*x; } void tree(int x) { for(int i=1;i<=n;i++) if(mp[x][i]>=0) { a[i]=mp[x][i]; mp[x][i]=-1;mp[i][x]=-1; l[x]=i; tree(i); break; } for(int i=1;i<=n;i++) if(mp[x][i]>=0) { a[i]=mp[x][i]; mp[x][i]=-1;mp[i][x]=-1; r[x]=i; tree(i); break; } } int dp(int i,int j) { if(j==0)return 0; if(l[i]==0&&r[i]==0)return a[i]; if(f[i][j])return f[i][j]; for(int k=0;k<=j-1;k++) f[i][j]=max(f[i][j],dp(l[i],k)+dp(r[i],j-k-1)+a[i]); return f[i][j]; } int main() { n=read();q=read();q++; int b,c,d; for(int i=1;i<=n;i++) for(int j=1;j<=n;j++) mp[i][j]=-1; for(int i=1;i<n;i++) { b=read();c=read();d=read(); mp[b][c]=d;mp[c][b]=d; } tree(1); cout<<dp(1,q)<<endl; return 0; }
不明白哪里像树了,好像一个区间dp然后处理一下根找树就好了啊;
枚举根节点的时候为什么k从i开始枚举才对;
搞不懂,慢慢想,想出来再更新博客(逃)
AC代码

#include<iostream> #include<cstdio> using namespace std; const int N=50; typedef long long ll; ll n,f[N][N],gen[N][N]; void tree(int l,int r) { if(l>r)return; cout<<gen[l][r]<<" "; if(l==r)return; tree(l,gen[l][r]-1); tree(gen[l][r]+1,r); } int main() { scanf("%lld",&n); for(int i=1;i<=n;i++) { scanf("%lld",&f[i][i]); gen[i][i]=i; } for(int l=1;l<n;l++) { for(int i=1;i+l<=n;i++) { int j=i+l; for(int k=i;k<=j;k++) { int maxx=f[i][k-1]*f[k+1][j]+f[k][k]; if(f[i][k-1]==0)maxx=f[k+1][j]+f[k][k]; if(f[k+1][j]==0)maxx=f[i][k-1]+f[k][k]; if(maxx>f[i][j]) { f[i][j]=maxx; gen[i][j]=k; } } } } cout<<f[1][n]<<endl; tree(1,n); }
至此,8.8学习树形DP结束
牺牲放假时间学习;
昨晚七夕我还在码代码。
我。。。。。