HDU 6470：Count（矩阵快速幂）

Count

Time Limit: 6000/3000 MS (Java/Others)    Memory Limit: 65536/65536 K (Java/Others)
Total Submission(s): 1187    Accepted Submission(s): 433

Problem Description

Farmer John有n头奶牛.
某天奶牛想要数一数有多少头奶牛,以一种特殊的方式:
第一头奶牛为1号,第二头奶牛为2号,第三头奶牛之后,假如当前奶牛是第n头,那么他的编号就是2倍的第n-2头奶牛的编号加上第n-1头奶牛的编号再加上自己当前的n的三次方为自己的编号.
现在Farmer John想知道,第n头奶牛的编号是多少,估计答案会很大,你只要输出答案对于123456789取模.

Input

第一行输入一个T,表示有T组样例
接下来T行,每行有一个正整数n,表示有n头奶牛 (n>=3)
其中，T=10^4,n<=10^18

Output

共T行,每行一个正整数表示所求的答案

Sample Input

5
3
6
9
12
15

Sample Output

31
700
7486
64651
527023

 思路

给出递推式：f[i]=f[i-1]+2*f[i-2]+n^3

可以构造矩阵：

 

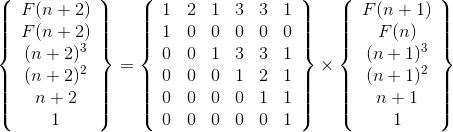
利用矩阵快速幂求解即可

代码

 1 #include <bits/stdc++.h>
 2 #define ll long long
 3 #define ull unsigned long long
 4 #define ms(a,b) memset(a,b,sizeof(a))
 5 const int inf=0x3f3f3f3f;
 6 const ll INF=0x3f3f3f3f3f3f3f3f;
 7 const int maxn=1e6+10;
 8 const ll mod=123456789;
 9 const int maxm=1e3+10;
10 using namespace std;
11 struct mart
12 {
13     ll m[6][6];
14 }unit;
15 mart mult(mart x,mart y)
16 {
17     mart ans;
18     for(int i=0;i<6;i++)
19     {
20         for(int j=0;j<6;j++)
21         {
22             ans.m[i][j]=0;
23             for(int k=0;k<6;k++)
24             {
25                 ans.m[i][j]+=x.m[i][k]*y.m[k][j];
26                 ans.m[i][j]%=mod;
27             }
28         }
29     }
30     return ans;
31 }
32 void init()
33 {
34     for(int i=0;i<6;i++)
35         unit.m[i][i]=1;
36 }
37 mart qpow(mart a,ll b)
38 {
39     init();
40     mart ans=unit;
41     while(b)
42     {
43         if(b&1)
44             ans=mult(ans,a);
45         a=mult(a,a);
46         b>>=1;
47     }
48     return ans;
49 }
50 ll slove(ll n)
51 {
52     mart a,b;
53     int res[6][6]={
54         1,2,1,3,3,1,
55         1,0,0,0,0,0,
56         0,0,1,3,3,1,
57         0,0,0,1,2,1,
58         0,0,0,0,1,1,
59         0,0,0,0,0,1,
60     };
61     for(int i=0;i<6;i++)
62         for(int j=0;j<6;j++)
63             a.m[i][j]=1LL*res[i][j];
64 
65     b.m[0][0]=2;
66     b.m[1][0]=1;
67     b.m[2][0]=8;
68     b.m[3][0]=4;
69     b.m[4][0]=2;
70     b.m[5][0]=1;
71     mart c=mult(qpow(a,n-2),b);
72     return c.m[0][0]%mod;
73 }
74 int main(int argc, char const *argv[])
75 {
76     #ifndef ONLINE_JUDGE
77         freopen("/home/wzy/in.txt", "r", stdin);
78         freopen("/home/wzy/out.txt", "w", stdout);
79         srand((unsigned int)time(NULL));
80     #endif
81     int t;
82     scanf("%d",&t);
83     ll n;
84     while(t--)
85     {
86         scanf("%lld",&n);
87         if(n==1||n==2)
88             printf("%lld\n",n);
89         else
90             printf("%lld\n",slove(n));
91     }
92     #ifndef ONLINE_JUDGE
93         cerr<<"Time elapsed: "<<1.0*clock()/CLOCKS_PER_SEC<<" s."<<endl;
94     #endif
95     return 0;
96 }

 

posted @ 2019-08-18 17:42  友人-A  阅读(243)  评论(0)  编辑  收藏  举报