并查集+线段树——luoguP4246 [SHOI2008]堵塞的交通

luogu题目链接

由于题目难以具体概括就不简述了qwq

70pts.做法

（为什么是70pts开始呢因为考试的时候写的是70pts的做法）
首先我们很容易注意到两点：

• 若A与B直连道路open，那么A与 与B联通的地方也能互相到达
• 若A与B直连道路close，那么A与B不一定不连通
  说到联通，就能想到并查集咯，对于一条道路的open操作，很容易进行常规并查集操作维护，而对于每一个ask，直接查询是否联通即可。但close该如何处理？最最最简单的方法——暴力。对于删除的边，我们对于两个顶点分别BFS（当然如果第一次BFS时发现两点依然联通则无需再次BFS），并重新设置代表点。这样的话70pts（luogu端）即可拿到70pts。

70pts.code

#include<iostream>
#include<cstdio>
#include<cstring>
#define swo(a,b)	a^=b^=a^=b
using namespace std;
const int N=2e5+5;
int C,f[N<<1],st[N<<1],to[N][5];
bool vis[N<<1];
string opt;
inline int find(int x)	{return f[x]==x ? x : f[x]=find(f[x]);}
inline void clo(int x,int y){
	for(int i=1;i<=2*C;i++)	vis[i]=0;
	for(int i=1;i<=3;i++)
		if(to[x][i]==y){
			to[x][i]=-1;
			break;
		}
	for(int i=1;i<=3;i++)
		if(to[y][i]==x){
			to[y][i]=-1;
			break;
		}
	if(find(y)==x)	swo(x,y);
	int head=0,tail=1;
	st[tail]=x;vis[x]=1;
	while(head<tail){
		int u=st[++head];
		for(int i=1;i<=3;i++)
			if(!vis[to[u][i]]&&to[u][i]!=-1){
				vis[to[u][i]]=1;
				if(to[u][i]==y){
					f[find(y)]=x;return;
				}
				st[++tail]=to[u][i];
			}
		f[u]=x;
	}
	head=0,tail=1;
	st[tail]=y;vis[y]=1;
	while(head<tail){
		int u=st[++head];
		for(int i=1;i<=3;i++)
			if(!vis[to[u][i]]&&to[u][i]!=-1){
				vis[to[u][i]]=1;
				st[++tail]=to[u][i];
			}
		f[u]=y;
	}
}
int main(){
//	freopen("traffic.in","r",stdin);
//	freopen("traffic.out","w",stdout);
	scanf("%d",&C);
	for(int i=1;i<=2*C;i++)	f[i]=i,to[i][1]=to[i][2]=to[i][3]=-1;
	while(1){
		cin>>opt;
		if(opt[0]=='E')	break;
		int r1,c1,r2,c2;
		scanf("%d%d%d%d",&r1,&c1,&r2,&c2);
		int x=c1+(r1-1)*C;
		int y=c2+(r2-1)*C;
		if(opt[0]=='O'){
			int fx=find(x);
			int fy=find(y);
			f[fy]=fx;
			for(int i=1;i<=3;i++)
				if(to[x][i]==-1){
					to[x][i]=y;
					break;
				}
			for(int i=1;i<=3;i++)
				if(to[y][i]==-1){
					to[y][i]=x;
					break;
				}
		}else	if(opt[0]=='C'){
			clo(x,y);
		}else{
			if(find(x)==find(y))	printf("Y\n");
			else	printf("N\n");
		}
	}
	return 0;
}

100pts.做法

(借鉴luogu一篇并查集题解)
按照题意，我们可以得到这么一张图，我们对于整个交通图给它标号

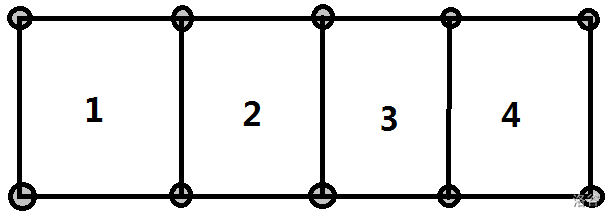
对于每一个单元格，我们定义它的周围的序号如下

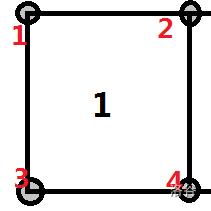
那么我们维护好每一个单元格的连通性就可以了（因为可以合并嘛）

• 维护： 若当前Open城市有同一个C ，那么我们需要维护左右两边的单元格，我们把左边单元格的3-4和右边单元格的1-2合并，就标志着C这条边是联通的。 对于Open城市处于两个不同的C ，把两个C中间的单元格的左右两个竖边连起来：在第一行的连1-3，第二行的连2-4。这样可以保证竖边的连通性（即保证询问的时候不出错，不理解就手动画一个）。
• 询问：（默认第一个城市在第二个城市的左边或上面），显然，如果直接从当前第一个城市走到第二个城市，比将第一个城市与第二个城市 分别 移到最左边不能再移动的地方和最右边不能再移动的地方的路径一定更少，所以我们可以考虑将第一个城市移到最左边不能再移动的地方（这里指同一行），第二个城市移到最右边不能再移动的地方，这期间的路径状态我们可以合并成一个单元格。再对走法枚举判定就好。

100pts.code

#include<iostream>
#include<cstdio>
#define lc k<<1
#define rc k<<1|1
using namespace std;
const int N=1e5+5;
int c,r1,r2,c1,c2,con[N][5];
string str;
struct node{
	int l,r,uf[5];
}a[N<<2];
inline int gi(){
	char ch;int res=0,fl=1;
	while((ch=getchar())&&(ch<'0'||ch>'9'))
		if(ch=='-')	fl=-1;
	res=ch-'0';
	while((ch=getchar())&&ch>='0'&&ch<='9')
		res=res*10+ch-'0';
	return res*fl;
}
inline void build(int k,int l,int r){
	a[k].l=l;a[k].r=r;
	for(int i=1;i<=4;i++)	a[k].uf[i]=i;
	if(l==r)	return;
	int mid=l+r>>1;
	build(lc,l,mid);
	build(rc,mid+1,r);
}
inline int find(int x,int f[]){
	return f[x]==x ? x : f[x]=find(f[x],f);
}
inline void merge(int x,int y,int f[])	{f[find(y,f)]=find(x,f);}
inline node UpDate(node x,node y){
	node z;
	z.l=x.l;z.r=y.r;
	for(int i=1;i<=4;i++)	z.uf[i]=i;
	if(find(1,x.uf)==find(2,x.uf))	z.uf[2]=1;
	if(find(3,y.uf)==find(4,y.uf))	z.uf[4]=3;
	for(int i=1;i<=2;i++)
		for(int j=3;j<=4;j++)
			if(find(i,x.uf)==find(j,x.uf))
				for(int k=3;k<=4;k++)
					if(find(j-2,y.uf)==find(k,y.uf))
						merge(i,k,z.uf);
		return z;
}
inline node query(int k,int l,int r,int x,int y){
	if(x<=l&&r<=y)	return a[k];
	int mid=l+r>>1;
	if(y<=mid)	return query(lc,l,mid,x,y);
	else	if(x>mid)	return query(rc,mid+1,r,x,y);
	else	return UpDate(query(lc,l,mid,x,y),query(rc,mid+1,r,x,y));
}
inline void update(int k,int l,int r,int x){
	if(l==x&&r==x){
		for(int i=1;i<=4;i++)	a[k].uf[i]=i;
		if(con[x][1])	merge(1,3,a[k].uf);
		if(con[x][2])	merge(2,4,a[k].uf);
		if(con[x][3])	merge(1,2,a[k].uf);
		if(con[x+1][3])	merge(3,4,a[k].uf);
		return;
	}
	int mid=l+r>>1;
	if(x<=mid)	update(lc,l,mid,x);
	else	update(rc,mid+1,r,x);
	a[k]=UpDate(a[lc],a[rc]);
}
int main(){
	c=gi();
	build(1,1,c-1);
	while(1){
		cin>>str;
		if(str[0]=='E')	break;
		r1=gi();c1=gi();r2=gi();c2=gi();
		if(str[0]=='A'){
			if(c1==c2){
				if(con[c1][3])	{printf("Y\n");continue;}//
				if(c1>1){
					node tmp=query(1,1,c-1,1,c1-1);
					if(find(3,tmp.uf)==find(4,tmp.uf))	{printf("Y\n");continue;}
				}
				if(c1<c){
					node tmp=query(1,1,c-1,c1,c-1);
					if(find(1,tmp.uf)==find(2,tmp.uf))	{printf("Y\n");continue;}
				}
				printf("N\n");
			}else{
				node tmp=query(1,1,c-1,min(c1,c2),max(c1,c2)-1);
				if(min(c1,c2)>1){
					node tmp1=query(1,1,c-1,1,min(c1,c2)-1);
					if(find(3,tmp1.uf)==find(4,tmp1.uf))	merge(1,2,tmp.uf);
				}
				if(max(c1,c2)<c){
					node tmp2=query(1,1,c-1,max(c1,c2),c-1);
					if(find(1,tmp2.uf)==find(2,tmp2.uf))	merge(3,4,tmp.uf);
				}
				if(c1<c2)	r2+=2;
				else	r1+=2;
				if(find(r1,tmp.uf)==find(r2,tmp.uf))	printf("Y\n");
				else	printf("N\n");
			}
		}else{
			if(c1==c2){
				con[c1][3]= (str[0]=='O');
				if(c1>1)	update(1,1,c-1,c1-1);
				if(c1<c)	update(1,1,c-1,c1);
			}else{
				con[min(c1,c2)][r1]= (str[0]=='O');
				update(1,1,c-1,min(c1,c2));
			}
		}
	}
	return 0;
}