基环树
written on 2022-07-20
（注：本文主要引自李煜东算法竞赛进阶指南）
先给出几个概念：
- 基环树
众所周知树的性质，即对于一个有 \(n\) 个节点的树，必定保证有 \(n-1\) 条边（无向边）。反过来，对于一个由 \(n-1\) 条无向边组成的连通图，必定是一棵树。据此，明显的，对于一个有 \(n\) 个结点 \(n\) 条边的无向连通图，必定是在一棵树上的任意两个节点之间连一条边构成的。我们把 \(n\) 个节点 \(n\) 条边的无向连通图，就称为基环树。
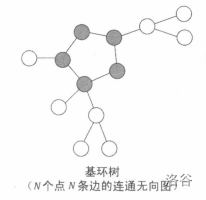
- 基环树森林
基环树森林可以视作是许多基环树的集合。基环树森林同样是 \(n\) 个节点 \(n\) 条边，但不一定保证连通。
- 内向树/外向树
可以视作有向图中的基环树吧，同样是 \(n\) 个节点 \(n\) 条边，不过这里的边是有向边，内向树中每个点有且仅有一条出边，外向树中每个点有且仅有一条入边。
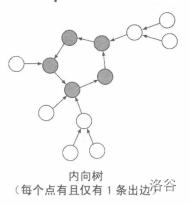
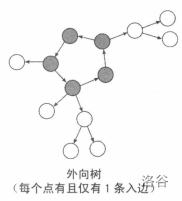
- 内向树/外向树森林
类似的，不多解释了。
基环树最引人注目的地方在于 \(n\) 个节点，\(n\) 条边。
基环树问题的一般解决方法：
先找出图中唯一的环，然后将环视作广义的“树的根节点”，然后把除了环之外的部分按照树来处理。最后统筹答案。
困了，具体的例题之类的明天上午再补咯。。
隔了两天回来补锅了
首先要声明一点，基环树作为一种不固定的多变的结构，变化很多，在遇到不同的基环树题时，第一步是观察数据类型，判断是否为基环树，或者说是内向树还是外向树，然后拆成非环和环两部分求解，接下来的具体情况，完全就要靠个人的分析了。
看一下考试时的例题。
具体的内部思路就不讲了，需要自己认真思考，但是，在拿到题目审完题后，应当要发现数据的一个特性，每个点只有一条出边，同时，\(n\) 个点 \(n\) 条边，因此可以直接下结论，这是一片内向树森林。根据这个特性，我们先处理出非环部分，对题目信息进行一定的转化，然后对环的部分单独分析思考即可。
题目变化多端，写这篇博客只是为了让自己以后能敏感地判断出基环树这种结构，至于题目能不能做出来，还要看悟性了。
