Day 28 动态规划part01| LeetCode 509.斐波那契数,70.爬楼梯,746.使用最小花费爬楼梯
理论基础
-
包含题目类别:基础类(斐波那契、爬楼梯)、背包问题、打家劫舍、股票问题、子序列问题
-
解题关键
- DP数组定义以及下标的含义
- 递推公式
- DP数组如何初始化
- 遍历顺序
- 打印DP数组
509.斐波那契数
class Solution {
public int fib(int n) {
if(n<=1) return n;
//dp数组:dp[i]--第i个斐波那契数数值
int []dp=new int[n+1];
//递推公式-- dp[i]=dp[i-1]+dp[i-2];
//dp数值初始化-- dp[0]=1,dp[1]=1
dp[0]=0;
dp[1]=1;
//确定遍历顺序-- 从前向后
for(int i=2;i<=n;i++)
{
dp[i]=dp[i-1]+dp[i-2];
}
//打印dp数组
return dp[n];
}
}
70.爬楼梯
class Solution {
public int climbStairs(int n) {
if(n==1) return 1;
if(n==2) return 2;
//dp数组:dp[i]--第i层有几种爬法
int []dp=new int[n+1];
//递推公式--dp[i]=dp[i-1]+dp[i-2];
//dp数值初始化--
dp[1]=1;
dp[2]=2;
//确定遍历顺序--
for(int i=3;i<n+1;i++)
{
dp[i]=dp[i-1]+dp[i-2];
}
//打印dp数组
return dp[n];
}
}
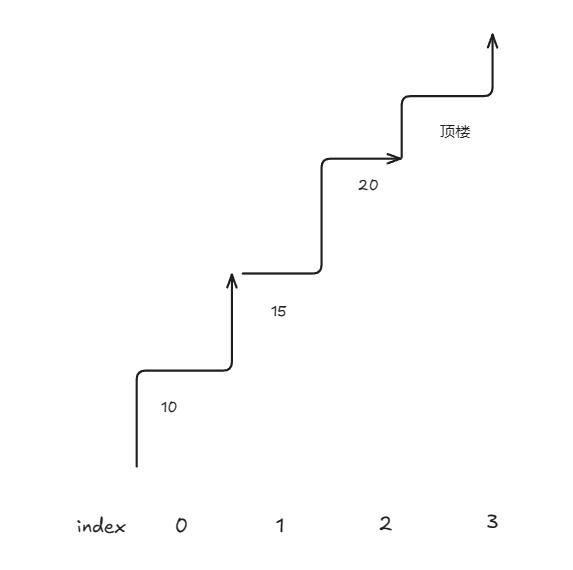
746.使用最小花费爬楼梯
class Solution {
public int minCostClimbingStairs(int[] cost) {
//dp数组 -- 到达下标i,所需花费为dp[i]
int []dp=new int[cost.length+1];
//递推公式-- dp[i]=Math.min(dp[i-1]+cost[i-1],dp[i-2]+cost[i-2]);
//dp数值初始化--默认从0/1开始 不花费
dp[0]=0;
dp[1]=0;
//确定遍历顺序--
for(int i=2;i<=cost.length;i++)
{
dp[i]=Math.min(dp[i-1]+cost[i-1],dp[i-2]+cost[i-2]);
}
//打印dp数组
return dp[cost.length];
}
}