利用Tensorflow实现线性回归
参考:https://www.jianshu.com/p/5cb93290fa85
本文介绍用tensorflow实现线性回归,以简单回归(两个参数)为例:y = W*x + b。大体的方法是通过Python在二维空间中创建数据,然后我会要求Tensorflow在这些点上寻找最合适的直线。线性回归问题属于监督学习,我们在模型学习过程中用到了数据和输出值。
第一步:导入numpy,创建数据。如下代码所示,我们基于关系y=0.1x+0.3生成了点。
import numpy as np
num_points=1000
vectors_set=[]
for i in range(num_points):
x1=np.random.normal(0.0,0.55)
y1=x1*0.1+0.3+np.random.normal(0.0,0.33)
vectors_set.append([x1,y1])
x_data=[v[0] for v in vectors_set]
y_data=[v[1] for v in vectors_set]
另外,用可视化工具来查看生成的数据,这里用matplotlib来画图(linux通过pip3 install matplotlib来安装,安装失败可能的原因是网络问题,可以采用换源来解决,我用阿里云的源安装成功)
import matplotlib.pyplot as plt
plt.plot(x_data,y_data,'ro',label='Original data')
plt.legend()
plt.show()
图形如下:
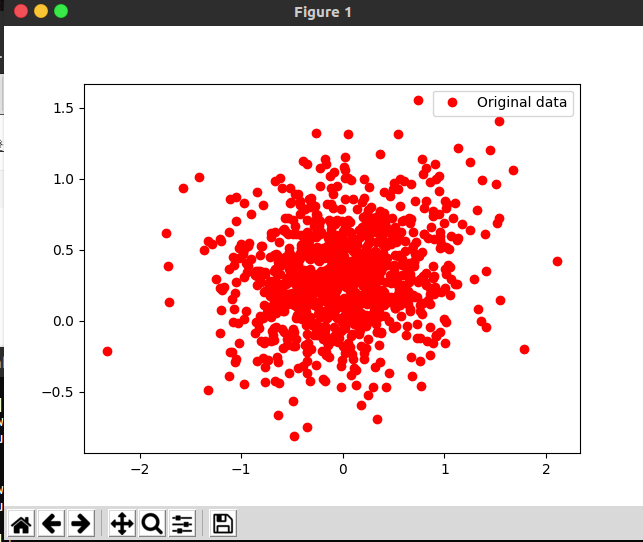
第二步,训练我们的学习算法,以便能够获得从输入数据x_data估计出的输出值y。目标是生成Tensorflow代码,找到最佳的参数W和b,它来自输入数据x_data,将其拟合到y_data,我们知道W应接近0.1,b应接近0.3,但Tensorflow并不知道,它需要通过学习来得到。即通过减小我们给定的损失函数来实现,这里损失函数采用均方误差。
首先,创建3个变量W,b,y:
import tensorflow as tf
W=tf.Variable(tf.random_uniform([1],-1.0,1.0))
b=tf.Variable(tf.zeros([1]))
y=W*x_data+b
然后,定义损失函数:
loss=tf.reduce_mean(tf.square(y-y_data))
之后通过梯度下降的优化算法,它接受由一组参数定义的函数,它以一组初始参数值开始,并迭代地移向一组使函数最小的值。 在函数梯度的负方向上移动来实现迭代式最小化。 通常计算距离平方来确保它是正的并且使误差函数可微分以便计算梯度。语句如下:
optimizer=tf.train.GradientDescentOptimizer(0.5)
train=optimizer.minimize(loss)
上面参数0.5是学习率,学习率参数控制每次迭代期间 TensorFlow 的每一步的下降程度。 如果我们引入的参数太大,我们可能会越过最小值。 但是,如果我们让 TensorFlow 采取较小步骤,则需要多次迭代才能达到最小值。
第三步,运行算法。首先对参数进行初始化:
init=tf.initialize_all_variables()
sess=tf.Session()
sess.run(init)
然后就是具体的迭代过程,这里迭代次数为8:
for step in range(8):
sess.run(train)
print(step,sess.run(W),sess.run(b))
第四步,通过图形展示最终结果:
plt.plot(x_data,y_data,'ro',label='Original data')
plt.plot(x_data,sess.run(W)*x_data+sess.run(b))
plt.legend()
plt.show()
结果如下:
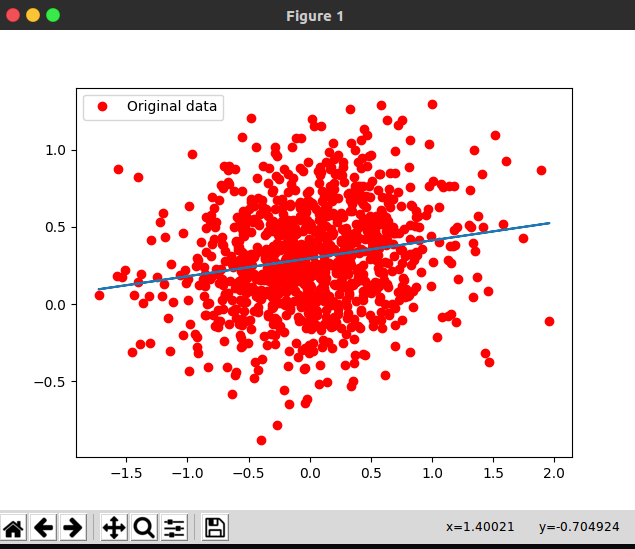
完整代码:
import numpy as np import matplotlib.pyplot as plt import tensorflow as tf num_points=1000 vectors_set=[] for i in range(num_points): x1=np.random.normal(0.0,0.55) y1=x1*0.1+0.3+np.random.normal(0.0,0.33) vectors_set.append([x1,y1]) x_data=[v[0] for v in vectors_set] y_data=[v[1] for v in vectors_set] W=tf.Variable(tf.random_uniform([1],-1.0,1.0)) b=tf.Variable(tf.zeros([1])) y=W*x_data+b loss=tf.reduce_mean(tf.square(y-y_data)) optimizer=tf.train.GradientDescentOptimizer(0.5) train=optimizer.minimize(loss) init=tf.initialize_all_variables() sess=tf.Session() sess.run(init) for step in range(8): sess.run(train) print(step,sess.run(W),sess.run(b)) plt.plot(x_data,y_data,'ro',label='Original data') plt.plot(x_data,sess.run(W)*x_data+sess.run(b)) plt.legend() plt.show()
当然,你也可以在迭代过程中画出每次迭代的图形。



