poj1182（带权并查集）

题目链接：http://poj.org/problem?id=1182

题意：题目告诉有  3  种动物，互相吃与被吃，现在告诉你  m  句话，其中有真有假，叫你判断假的个数  (  如果前面没有与当前话冲突的，即认为其为真话  )。每句话开始都有三个数 D A B，当D = 1时，表示A 和B是同类，当D = 2时表示A 吃 B。

思路：

想了好久也没有思路，数据量这么大，感觉只能用并查集来完成，之后参考了巨巨的博客：https://www.cnblogs.com/liuxin13/p/4668205.html。

不禁赞叹，真的是好题啊。好了，这道题是一个带权并查集的题。对于每一句话，首先可能出现直接能判定为假的情况，即输入的数有大于n的或者D=2且A=B时。之后就需要并查集了。不访设A->B的关系中0表示同类、1表示A吃B、2表示A被B吃。则输入的D减一后即代表A->B表示的关系，现在就将需要把有关系的点并在一起，用root[i]表示点i的祖先，f[i]表示点i与其祖先的关系，可能为0，1，2。

接下来先推一个公式：

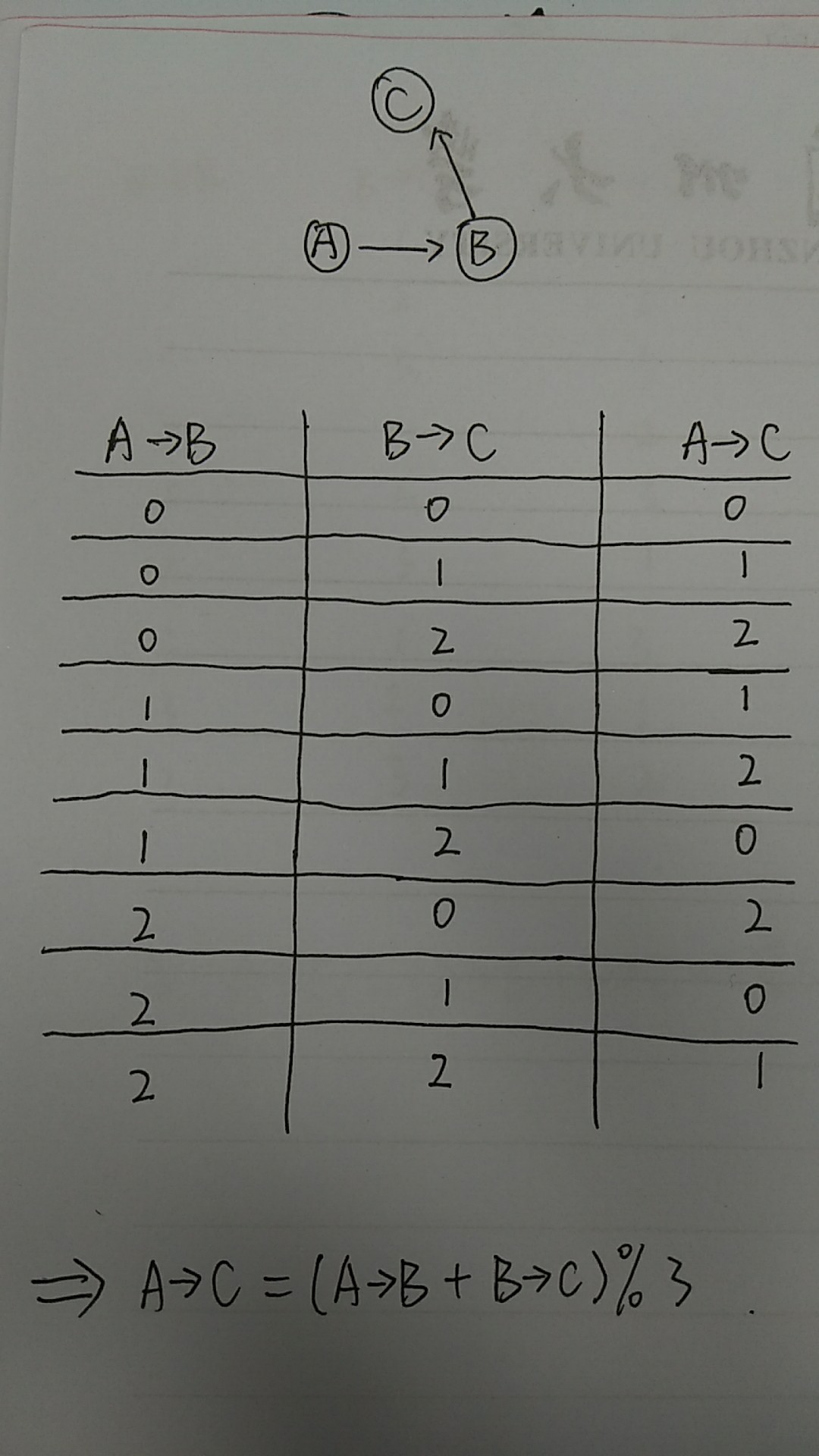
这样题目就可以继续进行了。输入d a b，用ra，rb表示a，b的祖先。若能直接判断为假话，则++res，继续下一句话，否则：

1.ra!=rb：那么将a，b合并。路径：root[rb]=ra。关系：f[rb]=rb->ra=(rb->a+a->ra)%3=((6-a->b-b->rb)%3+a->ra)%3=(6-a->b-b->rb+a->ra)%3=(6-(d-1)+f[a]-f[b])%3。

2.ra==rb：查询a->b是否等于(d-1)。判断f[a]==((d-1)+f[b])%3是否成立，若不成立则为错话。

在getr函数中要路径压缩和权值压缩（看代码，由上面推的公式就明白了）。

详见代码：

#include<cstdio>
using namespace std;

int n,k,res,d,a,b;
int root[50005],f[50005];

int getr(int kk){
    if(root[kk]==kk) return kk;
    else{
        int tmp=root[kk];
        root[kk]=getr(root[kk]);
        f[kk]=(f[kk]+f[tmp])%3;
        return root[kk];
    }
}

int main(){
    scanf("%d%d",&n,&k);
    for(int i=1;i<=n;++i)
        root[i]=i,f[i]=0;
    while(k--){
        scanf("%d%d%d",&d,&a,&b);
        int ra=getr(a),rb=getr(b);
        if(a>n||b>n||(d==2&&a==b))
            ++res;
        else if(ra==rb){
            if(f[a]!=(d-1+f[b])%3)
                ++res;
        }
        else{
            root[rb]=ra;
            f[rb]=(6-(d-1)+f[a]-f[b])%3;
        }
    }
    printf("%d\n",res);
    return 0;
}