矩阵乘法
矩阵乘法
不知道提高组会不会考,也要学把
贴一张别人的图:

裸的矩乘还挺简单的,三重循环
A*B 的最终矩阵是 A的行,B的列的规模,A的列和B的行是一样的
矩乘最基本的应用:斐波那契数列的优化
因为普通的要O(n),所以要考虑转化为幂的形式,这样可以用快速幂快速求解。(这其实也是一般套路吧,都要构造单位矩乘,这是难点)
我们发现:
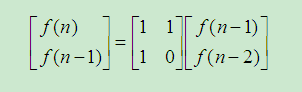
进一步,得出公式:

一种做法:预处理出幂次为32(或者其他也行)以内的矩阵幂的表,
对于K次:大于32的拿来减,小于等于32的进行二进制快速幂的思想。
如果数据是在太大,则可以预处理更大的表,如果空间够
或者干脆直接:矩阵快速幂OK啦
代码不贴了吧:网上很多(好吧还是贴一份吧)

1 ///求解fac(n)%100000,其中n为大于等于3的正整数 2 #include<stdio.h> 3 #include<math.h> 4 long long fac_tmp[6][4]={ ///存放矩阵次幂 5 ///位置:00 01 10 11 6 {24578,78309,78309,46269}, ///32次幂%100000 7 {1597,987,987,610}, ///16次幂%100000 8 {34,21,21,13}, ///8次幂%100000 9 {5,3,3,2}, ///4次幂%100000 10 {2,1,1,1}, ///2次幂%100000 11 {1,1,1,0}, ///1次幂%100000 12 }; 13 void fac(int); 14 15 int main() 16 { 17 int n; 18 scanf("%d",&n); 19 fac(n); 20 return 1; 21 } 22 23 void fac(int k) ///k>=3 24 { 25 int i; 26 long long t00=1,t01=1,t10=1,t11=0; ///表示矩阵的1次幂 27 long long a,b,c,d; 28 k=k-3; ///公式中是n-2次幂,(t00,t01,t10,t11)表示1次幂。所以一共减3次 29 for(i=k;i>=32;i=i-32) ///对于大于等于32的k; 30 { 31 a=(t00*fac_tmp[0][0]+t01*fac_tmp[0][2])%100000; 32 b=(t00*fac_tmp[0][1]+t01*fac_tmp[0][3])%100000; 33 c=(t10*fac_tmp[0][0]+t11*fac_tmp[0][2])%100000; 34 d=(t10*fac_tmp[0][1]+t11*fac_tmp[0][3])%100000; 35 t00=a; t01=b; t10=c;t11=d; 36 } 37 38 i=4; 39 while(i>=0) ///对于小于32的k(16,8,4,2,1); 40 { 41 if(k>=(long long)pow(2,i)) ///如果k大于某一个2的次幂 42 { 43 44 a=(t00*fac_tmp[5-i][0]+t01*fac_tmp[5-i][2])%100000; ///(5-i):矩阵的2的i次幂在数组fac_tmp中的位置为fac_tmp[5-i] 45 b=(t00*fac_tmp[5-i][1]+t01*fac_tmp[5-i][3])%100000; 46 c=(t10*fac_tmp[5-i][0]+t11*fac_tmp[5-i][2])%100000; 47 d=(t10*fac_tmp[5-i][1]+t11*fac_tmp[5-i][3])%100000; 48 t00=a; t01=b; t10=c;t11=d; 49 k=k-(int)pow(2,i); 50 } 51 i--; 52 } 53 54 a=(t00*2+t01*1)%100000; 55 printf("%lld\n",a); 56 }
fighting fighting fighting!!!




