有限自动机
有限自动机的概念
有限自动机可分为确定的有限自动机(Deterministic finite automata, DFA)和不确定的有限自动机(Nondeterministic finite automata, NFA)。区别在于转移函数不同,DFA对每一个可能的输入只有一个状态的转移,BFA对每一个可能的输入可以有多个状态转移,接受到输入时从这多个状态转移中非确定地选择一个。在解答有限自动机问题时需构造状态转换图,确定起始状态和终止状态,问题便可以解决。
字符串转换整数 (atoi)
请你来实现一个 atoi 函数,使其能将字符串转换成整数。
首先,该函数会根据需要丢弃无用的开头空格字符,直到寻找到第一个非空格的字符为止。接下来的转化规则如下:
如果第一个非空字符为正或者负号时,则将该符号与之后面尽可能多的连续数字字符组合起来,形成一个有符号整数。
假如第一个非空字符是数字,则直接将其与之后连续的数字字符组合起来,形成一个整数。
该字符串在有效的整数部分之后也可能会存在多余的字符,那么这些字符可以被忽略,它们对函数不应该造成影响。
注意:假如该字符串中的第一个非空格字符不是一个有效整数字符、字符串为空或字符串仅包含空白字符时,则你的函数不需要进行转换,即无法进行有效转> 换。在任何情况下,若函数不能进行有效的转换时,请返回 0 。
提示:本题中的空白字符只包括空格字符 ' ' 。假设我们的环境只能存储 32 位大小的有符号整数,那么其数值范围为 [−231, 231 − 1]。如果数值超过> 这个范围,请返回 INT_MAX (231 − 1) 或 INT_MIN (−231) 。
根据题构造状态转换图,其中b表示空格blank,d表示数字,c表示符号(+/-),?表示其它字符。
状态转换图:
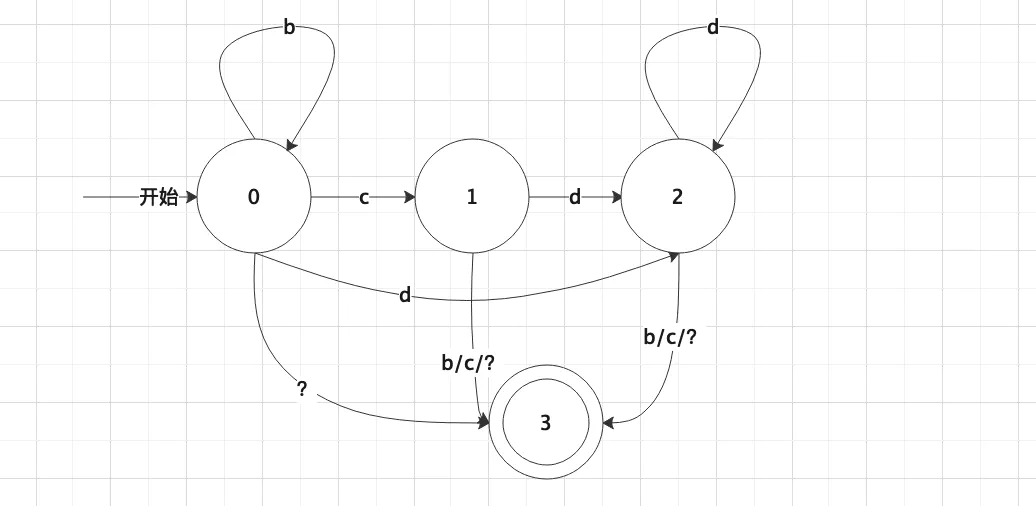
状态转换表如下:
| - | b | c | d | ? |
|---|---|---|---|---|
| 0 | 0 | 1 | 2 | 3 |
| 1 | 3 | 3 | 2 | 3 |
| 2 | 3 | 3 | 2 | 3 |
构造出状态转换表后,编程很简单,在本题中增加了对结果的判断,这个要注意。
class Solution:
def myAtoi(self, s: str) -> int:
state = [
{'b':0,'c':1,'d':2,'?':3},# 0
{'b':3,'c':3,'d':2,'?':3},# 1
{'b':3,'c':3,'d':2,'?':3}# 2
]
p,t = 0,''
res,sign = 0,1
for c in s:
if '0'<=c<='9':t = 'd'
elif c == ' ':t = 'b'
elif c in '+-':t = 'c'
else:t = '?'
if t in state[p]:
p = state[p][t]
if p == 1:
sign = 1 if c == '+' else -1
if p == 2:
res = res * 10 + ord(c) - ord('0')
if p == 3:
break
maxNumber,minNumber = 2**31 - 1,-2 ** 31
res *= sign
if res > maxNumber:res = maxNumber
if res < minNumber:res = minNumber
return res
表示数值的字符串
请实现一个函数用来判断字符串是否表示数值(包括整数和小数)。例如,字符串"+100"、"5e2"、"-123"、"3.1416"、"0123"都表示数值,但"12e"、"1a3.14"、"1.2.3"、"+-5"、"-1E-16"及"12e+5.4"都不是。
这一题可以看作是上一题的升级版,在于多了‘.’和‘e’两种转移方式,根据此题可以构造一个有限自动机,如图。
状态转换图:
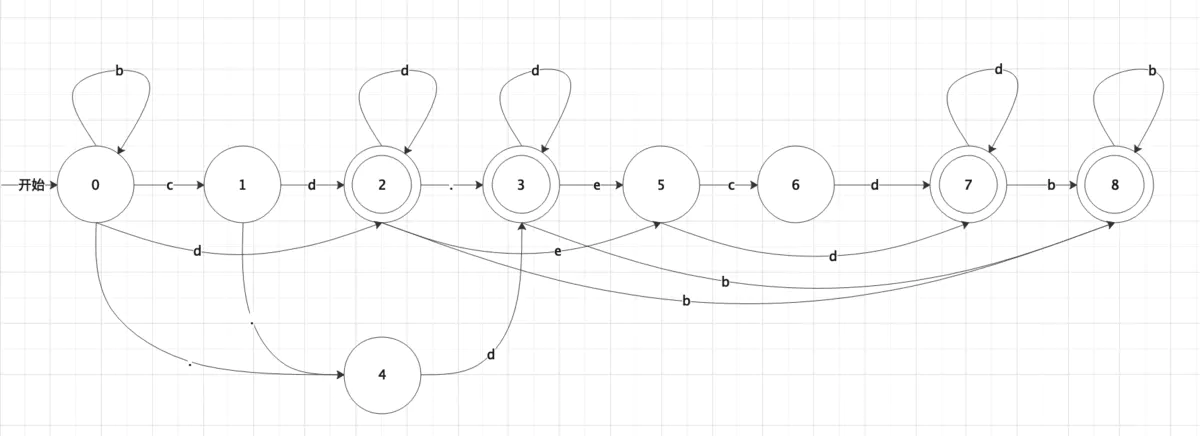
其中b表示空格blank,d表示数字,c表示符号(+/-)。根据有限自动机转移状态,判断最后是否结束。
| - | b | d | c | . | e |
|---|---|---|---|---|---|
| 0 | 0 | 2 | 1 | 4 | Φ |
| 1 | Φ | 2 | Φ | 4 | Φ |
| 2 | Φ | 2 | Φ | Φ | Φ |
| 3 | 8 | 3 | Φ | Φ | 5 |
| 4 | Φ | 3 | Φ | Φ | Φ |
| 5 | Φ | 7 | 6 | Φ | Φ |
| 6 | Φ | 7 | Φ | Φ | Φ |
| 7 | 8 | 7 | Φ | Φ | Φ |
| 8 | 8 | Φ | Φ | Φ | Φ |
如图构造状态转换表,接下来根据表编程。
class Solution:
def isNumber(self, s: str) -> bool:
# 有限自动机
state = [
{'b':0,'c':1,'d':2,'.':4},# 0
{'d':2,'.':4},# 1
{'d':2,'.':3,'b':8,'e':5},# 2
{'d':3,'e':5,'b':8},# 3
{'d':3},# 4
{'c':6,'d':7},# 5
{'d':7},# 6
{'d':7,'b':8},# 7
{'b':8}# 8
]
p,t = 0,''
for c in s:
if '0'<=c<='9':t = 'd'
elif c == ' ':t = 'b'
elif c in '.e':t = c
elif c in '+-':t = 'c'
else:t = '?'
if t in state[p]:p = state[p][t]
else:return False
# 判断是否终止
return p in [2,3,7,8]


