2023 春测

涂色游戏 Paint

题意

有一个 \(n\times m\) 的矩阵。现在进行 \(q\) 次操作，第 \(i\) 次操作将某行/某列的所有元素赋为 \(c_i\)，求所有操作之后的矩阵。\(T\) 组数据。\(\sum nm,\sum q\le 10^6\)。

解法

显然对于第 \(i\) 行第 \(j\) 列的元素，只需要讨论对第 \(i\) 行和第 \(j\) 列最后一次的赋值即可。

代码

点此查看代码

#include <bits/stdc++.h>
using namespace std;
const int maxn=100010;
int T,n,m,q,i,j,o,x,c;
int t[2][maxn],f[2][maxn];
int main(){
	freopen("paint.in","r",stdin);
	freopen("paint.out","w",stdout);
	scanf("%d",&T);
	while(T--){
		scanf("%d%d%d",&n,&m,&q);
		for(i=1;i<=q;++i){
			scanf("%d%d%d",&o,&x,&c);
			t[o][x]=i; f[o][x]=c;
		}
		for(i=1;i<=n;++i){
			x=t[0][i]; c=f[0][i];
			for(j=1;j<=m;++j) printf("%d ",t[1][j]>x?f[1][j]:c);
			putchar('\n');
		}
		memset(t[0]+1,0,n<<2); memset(f[0]+1,0,n<<2);
		memset(t[1]+1,0,m<<2); memset(f[1]+1,0,m<<2);
	}
	return 0;
}

幂次 Power

题意

求 \(1\sim n\) 内能被表示成 \(a^b\) 的形式的数的数量，其中 \(a,b\in\N_+;b\ge k\)。\(n\le 10^{18},k\le 100\)。

解法

特判 \(1\)，然后对于某个 \(a^b\) 和 \(\forall c|b\)，\(a^b\) 一定可以表示成 \((a^{\frac bc})^c\) 的形式，容斥即可。

代码

点此查看代码

#include <bits/stdc++.h>
using namespace std;
int k,i,j,p;
long long n,l,r,m,c,a,s,b[80];
int main(){
	freopen("power.in","r",stdin);
	freopen("power.out","w",stdout);
	scanf("%lld%d",&n,&k);
	if(k==1){
		printf("%lld",n);
		return 0;
	}
	for(i=70;i>=k;--i){
		for(l=1,r=n;l<=r;){
			m=(l+r)>>1;
			for(p=i,c=1;p;--p){
				if(c>n/m) break;
				c*=m;
			}
			if(p) r=m-1;
			else a=m,l=m+1;
		}
		for(j=i+i,--a;j<=70;j+=i) a-=b[j];
		b[i]=a; s+=a;
	}
	printf("%lld",s+1);
	return 0;
}

圣诞树 Tree

题意

有一个 \(n\) 个点的凸多边形，第 \(i\) 个顶点为 \((x_i,y_i)\)。现在需要在纵坐标最大且编号最小的点 \(k\) 出发遍历其他所有点，满足路径长度最小。输出某种合法的遍历顺序。\(n\le 10^3;|x_i|,|y_i|\le 10^7\)。

解法

考虑最后形成的路径一定不会存在交叉的情况，否则对于某条自交的路径一定可以调整为起终点相同的不自交路径，且由于三角形两边之和大于第三边可得调整后一定更优。

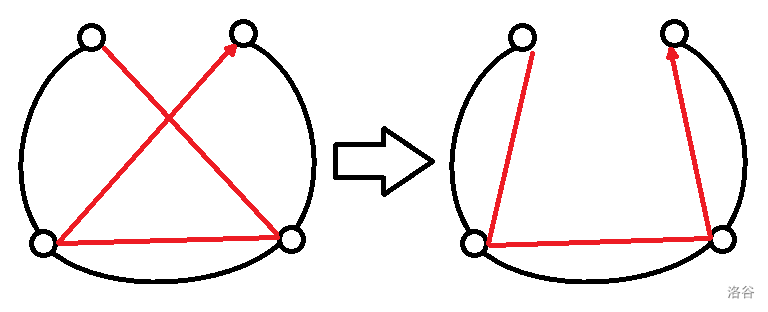
此时某条路径经过的点一定是一段段连续的区间（否则从区间外的点连向区间内一定会形成交点），所以从某个点出发能走到的点一定只能是区间两端的点。然后就可以使用区间 dp 计算答案了。

代码

点此查看代码

#include <bits/stdc++.h>
using namespace std;
#define ld long double
const int maxn=1010;
const int maxb=2010;
int n,i,j,k,l,r,b,p[maxn];
ld xs,xt,ys,yt,x[maxn],y[maxn];
ld d[maxb][maxb],dp[maxb][maxb][2];
inline void cmin(ld &x,ld y){if(x>y) x=y;}
int main(){
	freopen("tree.in","r",stdin);
	freopen("tree.out","w",stdout);
	scanf("%d",&n); b=(n<<1)-1;
	for(i=1;i<=b;++i) for(j=1;j<=b;++j) dp[i][j][0]=dp[i][j][1]=1e18;
	for(i=k=1;i<=n;++i){
		scanf("%Lf%Lf",x+i,y+i);
		if(y[i]>y[k]) k=i;
	}
	for(i=1;i<=n;++i){
		xs=x[i]; ys=y[i];
		for(j=1;j<=n;++j){
			if(i==j) continue; xt=xs-x[j]; yt=ys-y[j];
			d[i][j]=d[i+n][j]=d[i][j+n]=d[i+n][j+n]=sqrtl(xt*xt+yt*yt);
		}
	}
	dp[k][k][0]=dp[n+k][n+k][0]=0;
	for(i=1;i<n;++i){
		for(l=1,r=i;r<=b;++l,++r){
			if(l!=1) cmin(dp[l-1][r][0],min(dp[l][r][0]+d[l-1][l],dp[l][r][1]+d[l-1][r]));
			if(r!=b) cmin(dp[l][r+1][1],min(dp[l][r][0]+d[r+1][l],dp[l][r][1]+d[r+1][r])); 
		}
	}
	for(i=l=r=1;i<=n;++i){
		if(dp[i][i+n-1][0]<dp[l][l+n-1][r]) l=i,r=0;
		if(dp[i][i+n-1][1]<dp[l][l+n-1][r]) l=i,r=1;
	}
	for(i=n,p[n]=l+(n-1)*r;i>1;--i,p[i]=l+(i-1)*r){
		if(r) r=(dp[l][l+i-2][1]+d[l+i-2][l+i-1]<dp[l][l+i-2][0]+d[l][l+i-1]);
		else r=(dp[l+1][l+i-1][1]+d[l+i-1][l]<dp[l+1][l+i-1][0]+d[l+1][l]),++l;
	}
	for(i=1;i<=n;++i) printf("%d ",(p[i]-1)%n+1);
	return 0;
}

密码锁 Lock

题意

有一个 \(k\times n\) 的矩阵 \(a\)。可以进行任意次操作，每次操作选择某个 \(i\)，然后 \(\forall j\in[1,k]\)，将 \(a_{j,i}\) 赋为 \(a_{j\bmod k+1,i}\)。求经过若干操作后能得到的 \(a\) 的 \(\min\max_{j=1}^k(\max_{i=1}^n a_{j,i}-\min_{i=1}^n a_{j,i})\)。\(T\) 组数据。\(a_{i,j}\le 3\times 10^4;k\le 4;k\le 3\) 时 \(\sum n\le 1.5\times 10^5;k=4\) 时 \(\sum n\le 3\times 10^4\)。

解法

\(k=1\) 时直接输出 \(\max a_{i,j}-\min a_{i,j}\)。

\(k=2\) 时考虑 \(\max a_{i,j}\) 和 \(\min a_{i,j}\) 不能在同一行（否则答案一定会取到最大值），且对于 \(k\) 更大时该结论同样成立。此时可以将其他的 \(a_{1,i},a_{2,i}\) 的较大者换到 \(\max\) 所在行，将较小者换到 \(\min\) 所在行就可以同时达成最大化 \(\max\) 所在行的最小值同时最小化 \(\min\) 所在行的最大值。

\(k=3\) 时考虑在确定好 \(\max\) 和 \(\min\) 所在行时（有 \(O(k)\) 种取值），\(\max\) 和 \(\min\) 对应列在其他行的取值固定。然后考虑二分答案，设当前在确定答案是否大于 \(M\)，则需要让其他列在 \(\max\) 和 \(\min\) 所在行取值满足要求，同时需要存在第三行的某种取值方式使得所有列在第三行的取值均在某段长为 \(M\) 的区间内。此时可以把每种取值看成将区间左端点限制在某个范围内，可以看成有没有区间颜色数量为 \(n\)，使用双指针维护即可。

\(k=4\) 时仍然可以沿用上面的思路，但是需要所有列在第三行和第四行的取值均在某段长为 \(M\) 的区间内；将对应的取值化为平面直角坐标系上的点则问题变成了需要让所有种取值均在某个 \(M\times M\) 的矩形内。考虑将每列对应的矩形分别求并（可以使用单次 \(O(2^k)\) 的做法），然后用扫描线 + 线段树维护对应的并集，则线段树上只需要进行 \(O(nk)\) 次区间修改。

代码（暂缺）

点此查看代码