dp 综合

P4187 [USACO18JAN]Stamp Painting G

考虑在某次操作后一定会留下一段长为 $k$ 的同色段。同时可以通过对 $[1,k],[2,k+1],\cdots,[k-n+1,n],[k-n,n-1],\cdots,[p,p+k-1]$ 先后进行操作以控制这段同色段的位置，同时使得其他位置的颜色独立开来；所以某种方案只要出现了长为 $k$ 的同色段就一定合法。考虑在计算长为 $k$ 的同色段同时去重不太好处理，可以转换思路计算没有出现长为 $k$ 的同色段的方案数。设 $dp_{i,j}$ 为考虑填到 $i$ 位置，最后一段同色段的长度为 $j$ 的方案数，则转移有 $[j<k-1]\times dp_{i,j}\to dp_{i+1,j+1},(k-1)\times dp_{i,j}\to dp_{i+1,1}$ 。发现一定有 $\forall j>0,dp_{i,j+1}=dp_{i-1,j}$ ，相当于将整个数组右移一位，可以使用指针维护对应位，同时维护当前所有 dp 值之和即可。

代码

点此查看代码

 #include <bits/stdc++.h>
using namespace std;
const int maxn=1000010;
const int md=1000000007;
int n,m,k,p,s,dp[maxn]; 
inline int Pow(int d,int z){
	int r=1;
	do{
		if(z&1) r=(1LL*r*d)%md;
		d=(1LL*d*d)%md;
	}while(z>>=1);
	return r;
}
inline void Add(int &x,int y){x-=((x+=y)>=md)*md;}
int main(){
	scanf("%d%d%d",&n,&m,&k); 
	if(k==1){printf("%d",Pow(m,n));return 0;}
	dp[n]=s=m;
	for(p=n-1;p;--p){
		Add(s,dp[p]=(1LL*s*(m-1))%md);
		if(p+k-1<=n) Add(s,md-dp[p+k-1]);
	} 
	printf("%d",(Pow(m,n)+md-s)%md);
	return 0;
}

P7152 [USACO20DEC] Bovine Genetics G

考虑在形成的串划分成的不同子段中，一定满足两个因素：对于相邻两个相同的字符，中间一定有划分；且对于相邻的两段，一定有上一段的开头等于这一段的结尾。所以可以在扫到某个位置时，维护上一段的开头（也有这一段的开头），同时需要维护这一位的值，再 dp 转移。注意特判 dp 初值和整个串只被划分成一段的情况。

代码

点此查看代码

 #include <bits/stdc++.h>
using namespace std;
const int maxn=100010;
const int md=1000000007;
int i,j,k,p,c,n,dp[2][4][5][5];
char s[maxn]; auto *f=dp[0],*g=dp[1];
inline void Add(int &x,int y){x-=((x+=y)>=md)*md;}
void chg(int c){
	for(j=0;j<4;++j)
		for(k=0;k<5;++k)
			Add(g[c][c][k],f[j][k][j]),
			Add(g[c][c][k],f[j][k][4]);
	if(i==1) return;
	for(j=0;j<4;++j) if(j!=c) 
		for(k=0;k<4;++k)
			for(p=0;p<5;++p)
				Add(g[c][k][p],f[j][k][p]);
}
int main(){
	scanf("%s",s+1); 
	n=strlen(s+1); f[0][4][0]=1;
	for(i=1;i<=n;++i){
		if((c=s[i])=='A') chg(0);
		else if(c=='C') chg(1);
		else if(c=='G') chg(2);
		else if(c=='T') chg(3);
		else for(c=0;c<4;++c) chg(c);
		swap(f,g); memset(g,0,sizeof(dp[0]));
	}
	for(j=c=0;j<4;++j)
		for(k=0;k<4;++k)
			Add(c,f[j][k][j]),
			Add(c,f[j][k][4]);
	printf("%d",c); return 0;
}

P3578 [POI2014]LAM-Solar lamps

考虑将每个灯的位置按照 CF249D Donkey and Stars 的方法用光束的方向对应的单位向量表出，则问题变成了二维数点问题。注意夹角可能为 $0$ ，需要特判对应的情况（例如将第二个向量旋转 $90^{\rm o}$ ，查询能照到某盏灯的灯时只查询第二维相等的灯）。最开始的做法是二分出能照到第 $i$ 盏灯的 $k_i$ 盏灯亮起的初始时刻，使用树套树查询/修改，但是不是因为时间 $O(n\log^3 n)$ 就是因为空间 $O(n\log^2 n)$ 屡屡炸裂，不过优秀的 BIT + FHQ 做法可以在 Darkbzoj 上过掉。

考虑整体二分。设当前判断哪些灯能够在时间 $M$ 之前被点亮，则需要该灯的下标小于 $M$ ，或者是在时间 $M$ 之前点亮的，在该灯的左下角的灯数量是否足够。对于后者需要先将灯排序，将满足要求的灯顺序加入数据结构，然后在该灯对应的位置进行查询。

代码

点此查看代码

 #include <bits/stdc++.h>
using namespace std;
#define ll long long
const int maxn=200010;
int n,i,a,b,c,d,x,y,pt,lt,rt,mt; 
int C[maxn],dp[maxn],lq[maxn],rq[maxn]; 
ll lst; bool fl;
struct Vals{
	ll val; int idx;
	inline bool operator <(const Vals &p)const{return val<p.val;}
}A[maxn],B[maxn];
struct node{
	int ra,rb,cnt,idx;
	inline bool operator <(const node &p)const{
		if(ra!=p.ra) return ra<p.ra;
		return rb<p.rb; 
	}
}N[maxn],LN[maxn],RN[maxn];
inline void cmin(int &x,int y){if(x>y) x=y;}
inline void Add(int p,int d){
	if(fl) C[p]+=d;
	else for(;p<=n;p+=p&-p) C[p]+=d;
}
inline int Query(int p){
	if(fl) return C[p];
	int r=0;
	for(;p;p^=(p&-p)) r+=C[p];
	return r;
}
void Solve(int L,int R,int l,int r){
	if(l>r) return;
	if(L==R){
		while(l<=r) dp[N[l++].idx]=L;
		return;
	}
	sort(N+l,N+r+1); 
	int M=(L+R)>>1,lc=0,rc=0,m;
	for(i=l;i<=r;++i){
		if(N[i].idx<=M||(a=Query(N[i].rb))>=N[i].cnt)
			Add(N[i].rb,1),LN[++lc]=N[i];
		else N[i].cnt-=a,RN[++rc]=N[i];
	}
	i=l; m=l+lc-1;
	while(lc) Add((N[i++]=LN[lc--]).rb,-1);
	while(rc) N[i++]=RN[rc--];
	Solve(L,M,l,m); Solve(M+1,R,m+1,r);
}
int main(){
	scanf("%d%d%d%d%d",&n,&a,&b,&c,&d);
	if(1LL*a*d==1LL*b*c) fl=1,c=b,d=-a;
	if(1LL*a*d<1LL*b*c) pt=-1; else pt=1;
	for(i=1;i<=n;++i){
		scanf("%d%d",&x,&y); 
		N[i].idx=A[i].idx=B[i].idx=i;
		A[i].val=((1LL*x*d)-(1LL*y*c))*pt;
		B[i].val=((1LL*y*a)-(1LL*x*b))*pt;
	}
	for(i=1;i<=n;++i) scanf("%d",&N[i].cnt);
	sort(A+1,A+n+1); sort(B+1,B+n+1);
	x=1; lst=A[1].val; 
	for(i=1;i<=n;++i){
		while(A[i].val==lst&&i<=n) N[A[i++].idx].ra=x;
		if(i<=n) lst=A[i].val,N[A[i].idx].ra=++x;
	}
	x=1; lst=B[1].val;
	for(i=1;i<=n;++i){
		while(B[i].val==lst&&i<=n) N[B[i++].idx].rb=x;
		if(i<=n) lst=B[i].val,N[B[i].idx].rb=++x;
	}
	Solve(1,n,1,n);
	for(i=1;i<=n;++i) printf("%d ",dp[i]);
	return 0;
}

P6142 [USACO20FEB]Delegation P

首先考虑二分答案。设当前判断答案是否大于 $M$ ，考虑在每棵子树内该如何使答案最优。

考虑某个节点 $u$ 向父亲连的边在长度为多少的链上。此时在从下向上确认该条链使其最长时，考虑将从 $u$ 向上的链从 $u$ 的某个儿子对应的链转移上来（此时能留下的链长度有单调性）。如果 $u$ 有奇数个儿子，则可以直接二分留下的链的长度，合并其他儿子（可以直接双指针贪心匹配）；否则需要分两种情况考虑：如果直接从 $u$ 开始起一条新链，则需要其他所有儿子能匹配成功；否则需要贪心保留一段长度大于 $M$ 的长度最小的链，将对应的情况转为有奇数个儿子的情况。

代码

点此查看代码

 #include <bits/stdc++.h>
using namespace std;
const int maxn=100010;
int n,i,j,k,u,v,t,a,L,R,M;
int f[maxn],g[maxn],h[maxn];
int dp[maxn],d[maxn];
struct edge{int to,nxt;}E[maxn<<1];
bool Mat(){
	for(j=1,t=k>>1;j<=t;++j) if(g[j]+g[k+1-j]<M) break;
	return j<=t;
}
int Bin(){
	int a=0,l=1,r=i,m;
	while(l<=r){
		m=(l+r)>>1; k=0;
		for(j=1;j<=i;++j) if(j!=m) g[++k]=f[j];
		if(Mat()) r=m-1; else a=m,l=m+1;
	}
	return a;
}
bool dfs(int p,int fa){
	if(!d[p]){dp[p]=1;return 0;} int lp,to,nt=0; 
	for(lp=h[p];lp;lp=E[lp].nxt){
		if((to=E[lp].to)==fa) continue;
		if(dfs(to,p)) return 1; 
		if(dp[to]>=M&&dp[to]<=dp[nt]) nt=to;
	}
	for(i=0,lp=h[p];lp;lp=E[lp].nxt){
		if((to=E[lp].to)!=fa){
			f[++i]=dp[to];
			if(nt==to) nt=-i;
		}
	}
	sort(f+1,f+i+1); nt=-nt;
	if(p==1){
		if(d[p]&1){
			if(!nt) return 1;
			for(j=nt;j<=i;++j) f[j]=f[j+1]; --i;
		}
		memcpy(g+1,f+1,i<<2); k=i; return Mat();
	}
	if(d[p]&1){
		if(!(lp=Bin())) return 1;
		else dp[p]=f[lp]+1; return 0;
	}
	else{
		memcpy(g+1,f+1,i<<2);
		k=i; if(Mat()) return 1; 
		if(!nt){dp[p]=1; return 0;}
		for(j=nt;j<=i;++j) f[j]=f[j+1]; 
		--i; dp[p]=f[Bin()]+1; return 0;
	}
} 
int main(){
	scanf("%d",&n); 
	for(i=1;i<n;++i){
		scanf("%d%d",&u,&v);
		E[++t]={v,h[u]}; h[u]=t;
		E[++t]={u,h[v]}; h[v]=t;
		++d[u]; ++d[v]; --d[i+1];
	}
	dp[0]=1145141919;
	for(L=1,R=n;L<=R;){
		memset(dp+1,0,n<<2);
		M=(L+R)>>1;
		if(dfs(1,0)) R=M-1;
		else a=M,L=M+1;
	}
	printf("%d",a); return 0;
}

AT_joi2013ho5 バブルソート (Bubble Sort)

考虑交换某对元素后对答案的贡献：对于某个 $a_k$ ，在交换满足 $a_i>a_k>a_j$ 且 $i<j$ 的 $a_i,a_j$ 之后 $a_k$ 将会使答案减少 $2$ 。此时将 $a_i$ 变成 $1\sim i$ 内最大值， $a_j$ 变成 $j\sim n$ 内最小值一定不劣。注意可能有 $a_i/a_j=a_k$ 的情况，此时维护前缀最大值/后缀最小值时应该维护值相同的数，计算贡献时可以把对应贡献拆开成两部分，转化成对 $a_i>a_k\ge a_j$ 和 $a_i\ge a_k>a_j$ 的 $(i,j)$ 各加上 $1$ 。将 $(i,j)$ 看成平面直角坐标系上的点，则 $a_k$ 能对答案造成贡献时对应的 $i,j$ 一定都是对应前缀最大值和后缀最小值上连续的一段， $(i,j)$ 一定为一个矩形。此时直接扫描线处理即可。

代码

点此查看代码

 #include <bits/stdc++.h>
using namespace std;
const int maxn=100010;
int n,i,u,v,w,t,tn,tx; long long s=-1;
int l1[maxn],l2[maxn],rt[maxn],pe[maxn];
int a[maxn],b[maxn],c[maxn],pn[maxn],px[maxn];
struct node{
	int l,r,x,d;
	inline bool operator <(const node &a)const{return x<a.x;}
}N[maxn*4];
struct seg{int mx,add;}tr[maxn*4];
#define ls(p) p<<1
#define rs(p) p<<1|1
#define mx(p) tr[p].mx
#define add(p) tr[p].add
inline void pushup(int p){
	mx(p)=max(mx(ls(p)),mx(rs(p)));
}
inline void pushtag(int p,int d){
	mx(p)+=d; add(p)+=d;
}
inline void pushdown(int p){
	if(!add(p)) return;
	pushtag(ls(p),add(p));
	pushtag(rs(p),add(p));
	add(p)=0;
}
void change(int p,int l,int r,int L,int R,int d){
	if(L<=l&&R>=r){pushtag(p,d);return;}
	pushdown(p); int m=(l+r)>>1;
	if(L<=m) change(ls(p),l,m,L,R,d);
	if(R>m) change(rs(p),m+1,r,L,R,d);
	pushup(p); 
}
inline bool cmp(int x,int y){
	if(b[x]!=b[y]) return b[x]<b[y];
	return x<y;
}
inline void Add(int p){for(;p<=n;p+=p&-p) ++c[p];}
inline void Que(int p){for(s+=i-1;p;p^=p&-p) s-=c[p];}
int main(){
	scanf("%d",&n);
	for(i=1;i<=n;++i) scanf("%d",b+i),pe[i]=i;
	if(n==2){printf("%d",b[1]<b[2]); return 0;}
	sort(pe+1,pe+n+1,cmp);
	for(i=1;i<=n;++i,v=u) u=pe[i],a[u]=(tn+=(b[v]!=b[u]));
	for(i=1,u=0;i<=n;++i){
		Que(v=a[i]); Add(v); 
		if(i<n){
			if(i>1){
				l1[i]=lower_bound(px+1,px+tx+1,v)-px; 
				l2[i]=upper_bound(px+1,px+tx+1,v)-px; 
				if(l2[i]>tx) l2[i]=0; rt[i]=tx;
			}
			if(v>=u) px[++tx]=u=v;
		}
	}
	if(s<0){
		for(i=1;i<n;++i) if(a[i+1]==a[i]) break;
		printf("%d\n",i==n); return 0;
	}
	if(!s){printf("0\n");return 0;} 
	for(u=pn[1]=a[n],i=n-1,tn=1,++tx;i>1;--i){
		v=a[i];
		if(l2[i]){
			N[++t]={l2[i],rt[i],lower_bound(pn+1,pn+tn+1,v,greater<int>())-pn,1}; 
			++t; N[t]=N[t-1]; N[t].x=tn+1; N[t].d=-1;
		}
		if((w=upper_bound(pn+1,pn+tn+1,v,greater<int>())-pn)<=tn){
			N[++t]={l1[i],rt[i],w,1}; 
			++t; N[t]=N[t-1]; N[t].x=tn+1; N[t].d=-1;
		}
		if(v<=u) pn[++tn]=u=v; 
	}
	sort(N+1,N+t+1);
	for(i=1,u=0;i<=t;++i){
		change(1,1,tx,N[i].l,N[i].r,N[i].d);
		if(N[i+1].x!=N[i].x&&u<mx(1)) u=mx(1);
	}
	printf("%lld\n",s-u); return 0;
}

P5244 [USACO19FEB] Mowing Mischief P

~~刚开始时以为线的起点一定是原点~~

显然确定好 $S$ 之后， $S$ 内每个点被经过的顺序固定，且由于题目限制（线的两个端点必须每秒移动一个单位长度）可得从某个点到达另一个点时最优方案同样固定（扫过两点之间的整个矩形），则问题变成了选择尽量多个点且相邻点对应的矩形面积之和尽可能小。

令 $dp_{i,j}$ 表示选择了 $i$ 个点，最后一个点为 $j$ 的方案数，则转移为 $dp_{i,j}=\min_{X_k<X_i,Y_k<Y_i}(dp_{i-1,k}+w(k,i))$ ，其中 $w(k,i)=(X_i-X_k)(Y_i-Y_k)$ 。考虑将所有点按照 $X$ 排序，去掉 $X_k<X_i$ 的限制；同时对排序后的 $Y$ 预处理一遍 LIS，令 $L_i$ 为以 $i$ 结尾的 LIS 长度，则如果能从 $j$ 转移到 $i$ 则需要 $L_j=L_i-1$ ，去掉 $dp_{i,j}$ 的前一维。此时满足 $L_i=x$ 的 $Y_i$ 一定随对应 $X_i$ 的增加而减少，所以在 $X_i$ 从小到大枚举 $L_i=x$ 时，对应能转移来的点一定是 $X$ 连续的一段区间。

$(X_i-X_k)(Y_i-Y_k)$ 部分不好通过单调队列/斜率优化的方式优化。不过可以发现对于某组 $p_1,p_2,p_3,p_4$ （ $X_{p_1}>X_{p_2},X_{p_3}>X_{p_4},L_{p_1}=L_{p_2}=L_{p_3}-1=L_{p_4}-1$ ），如果 $w(p_1,p_3)<w(p_2,p_3)$ 则一定有 $w(p_1,p_4)<w(p_2,p_4)$ ，满足决策单调性。证明考虑下图中如果 $S_1+S_2<S_3$ 则一定有 $S_1<S_3+S_4$ 。

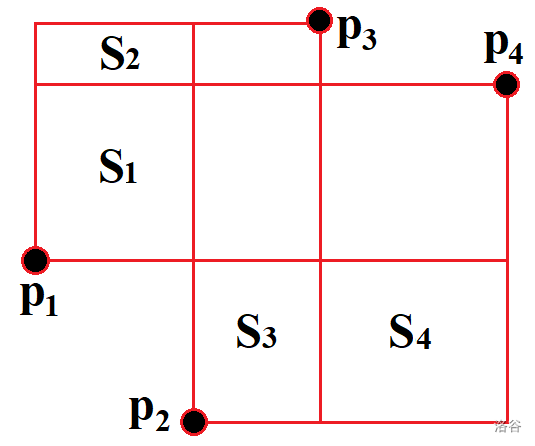
注意上述情况当且仅当有 $p_3,p_4$ 均能够从 $p_1,p_2$ 转移时才成立。考虑将能够转移到相同的某个区间决策拿出来进行决策单调性分治优化 dp。此时可以将决策区间建出线段树，将待求的每个 dp 值的合法决策区间放在线段树的 $O(\log)$ 个节点上；最后遍历线段树的所有节点进行 dp。

代码

点此查看代码

 #include <bits/stdc++.h>
using namespace std;
#define ll long long
const int maxn=200010;
const int maxt=1000010;
int n,i,j,u,t,l,L,R,kl,kr,c[maxt];
int f[maxn],x[maxn],y[maxn],p[maxn];
int px[maxn],py[maxn],xp[maxt]; ll dp[maxn];
inline void cmax(int &x,int y){if(x<y) x=y;}
inline void cmin(ll &x,ll y){if(y<x) x=y;}
inline bool cmp(const int &a,const int &b){
	if(f[a]!=f[b]) return f[a]<f[b];
	return y[a]>y[b];
}
inline void Add(int p,int d){
	for(;p<t;p+=p&-p) cmax(c[p],d);
}
inline int Que(int p){
	int r=0;
	for(;p;p^=p&-p) cmax(r,c[p]);
	return r;
}
inline ll w(int a,int b){
	return dp[a]+1LL*(px[b]-px[a])*(py[b]-py[a]);
}
vector<int> v[maxn<<2];
#define ls(p) p<<1
#define rs(p) p<<1|1
void cover(int p,int l,int r){
	if(L<=l&&R>=r){
		v[p].push_back(j);
		return;
	}
	int m=(l+r)>>1;
	if(L<=m) cover(ls(p),l,m);
	if(R>m) cover(rs(p),m+1,r); 
}
void Solve(int l,int r,int kl,int kr,vector<int> &v){
	if(l>r) return;
	int m=(l+r)>>1,u=v[m],km=kl; 
	ll a,ka=0x3f3f3f3f3f3f3f3f;
	for(j=kl;j<=kr;++j){
		if(px[j]>=px[u]||py[j]>=py[u]) continue; 
		if((a=w(j,u))<ka) ka=a,km=j;
	}
	cmin(dp[u],ka); 
	Solve(l,m-1,km,kr,v); 
	Solve(m+1,r,kl,km,v);
}
void dfs(int p,int l,int r){
	if(!v[p].empty()){
		Solve(0,v[p].size()-1,l,r,v[p]);
		v[p].clear();
	}
	if(l==r) return; int m=(l+r)>>1;
	dfs(ls(p),l,m); dfs(rs(p),m+1,r);
}
int main(){
	scanf("%d%d",&n,&t);
	for(i=1;i<=n;++i){
		scanf("%d%d",&u,y+i);
		xp[u]=p[i]=i; x[i]=u;
	}
	for(i=1;i<=t;++i){
		if(!(u=xp[i])) continue;
		Add(y[u],f[u]=Que(y[u])+1);
	}
	sort(p+1,p+(++n),cmp); 
	memset(dp+1,0x3f,n<<3);
	x[0]=y[0]=t; p[n+1]=1;
	for(i=l=1;i<=n;++i){
		px[i]=x[p[i]]; py[i]=y[p[i]];
		if(f[p[i+1]]!=f[p[i]]){
			L=R=kl;
			for(j=l;j<=i;++j){
				while(L<=kr&&py[L]>py[j]) ++L;
				while(R<kr&&px[R+1]<px[j]) ++R;
				cover(1,kl,kr);
			}
			dfs(1,kl,kr);
			kl=l; kr=i; l=i+1; 
		} 
	}
	printf("%lld",dp[n]);
	return 0;
}

P5156 [USACO18DEC]Sort It Out P

显然没有选的数一定不会因为选的数而改变相对的位置，所以这些数一定递增；同时在将某一个数排到对应位置时，一定不会使得之前排到对应位置的数满足左边的数比自己大/右边的数比自己更小；所以在对某个子集按照题中方法排好序的过程，一定对应了将它们单独排序然后归并到原序列内的过程。（此时选择任意一个递增子序列的补集一定满足条件）由此第一问的答案就是 $n-|\texttt{LIS}|$ 。

然后考虑使用选择的子集的补集的字典序确定好子集的字典序。此时对于子集 $s_1,s_2$ ，如果它们的补集 $c_1,c_2$ 的前 $p$ 位相同，而 $c_{1,p+1}<c_{2,p+1}$ ，则 $s_1,s_2$ 在 $1\sim c_{1,p+1}-1$ 内的部分均相同，而在下一位中 $s_2$ 取的是 $c_{1,p+1}$ ， $s_1$ 则需要取 $c_{1,p+1}$ 之后的元素（注意此时集合内的数从小到大排好序），所以 $c_1<c_2$ 对应了 $s_1>s_2$ ，第二问的答案就是取字典序第 $k$ 大的 LIS 的补集。

此时可以对于每个 $a_i$ ，先求出以其为结尾的 LIS 的长度 $f_i$ ，令 $S_i=\{j|f_j=i\}$ ，则每个 $S_i$ 内的元素的下标随值的增加而递减（同一层），此时 $S_i$ 每个元素在对应的 LIS 的后继一定是 $S_{i+1}$ 的某个区间（值和下标均需要更大），使用双指针求即可（注意中间可能出现大于 $k$ 的数并且可能溢出，需要特判这部分），最后求字典序第 $k$ 大的 LIS 可以通过试填每一位求出。

代码

点此查看代码

 #include <bits/stdc++.h>
using namespace std;
const int maxn=100010;
int n,i,j,l,r,d,u,x;
int c[maxn],h[maxn],a[maxn],nxt[maxn];
long long k,s,dp[maxn]; bool v[maxn];
inline void cmax(int &x,int y){if(y>x) x=y;}
inline void Add(int p){for(;p<=n;p+=p&-p) cmax(c[p],u);}
inline void Que(int p){for(u=0;p;p^=p&-p) cmax(u,c[p]); ++u;}
int main(){
	scanf("%d%lld",&n,&k);
	for(i=1;i<=n;++i){
		scanf("%d",&j); Que(a[i]=j); 
		nxt[i]=h[u]; h[u]=i; Add(j);
	}
	Que(n); printf("%d\n",n-(--u));
	for(j=h[u];j;j=nxt[j]) dp[j]=1;
	for(i=u-1;i;--i){
		for(l=nxt[0]=h[i+1],s=r=d=0,j=h[i];j;j=nxt[j]){
			while(nxt[r]>j) s+=dp[r=nxt[r]],d+=(dp[r]<0);
			for(x=a[j];l&&a[l]<x;l=nxt[l]) s-=dp[l],d-=(dp[l]<0);
			if(d||s>k) dp[j]=-1; else dp[j]=s; 
		}
	} 
	for(i=1,d=0;i<=u;++i){
		for(r=0,j=h[i];j;j=nxt[j]) c[++r]=j;
		while(r){
			j=c[r--]; if(j<d||a[j]<a[d]) continue;
			if(dp[j]<0||k<=dp[j]){v[a[d=j]]=1;break;}
			else k-=dp[j];
		}
	}
	for(i=1;i<=n;++i) if(!v[i]) printf("%d\n",i);
	return 0;
}

CF1193A Amusement Park

$\rm{From }$ $\rm{L}\color{red}{7\mathsf{-}56}$ $\rm .$

考虑将某个 DAG 的所有边反向之后得到的图仍然是一个 DAG，所以可以先求出总方案数再乘上 $\frac m2$ 即可得出答案。

考虑将得到的 DAG 拆分成若干层，此时分层的方案一定和边的定向方案一一对应。设 $dp_S$ 为 $S$ 点集的对应分层方案数，转移时初看有 $dp_S=\sum_{T\subseteq S}[\ T\ 是独立集\ ]dp_{S-T}$ ，然而可能有分层不合法的方案纳入贡献（某一层被拆分成了多层）。此时需要在加入某个独立集之后减去某个独立集被加两次的贡献。此时可以猜想需要乘上某个系数，令 $g_S$ 为转移时需要的 $S$ 的系数（ $dp_S=\sum_{T\subseteq S}[\ T\ 是独立集\ ]g_Tdp_{S-T}$ ），则在计算 $dp_S$ 转移时，新的一层为 $T$ 的对应方案数的系数为 $\sum_{T'\subseteq T,T'\ne\emptyset}g_{T'}$ ，需要这个值无论 $T$ 取何值时始终为 $1$ 。此时可以考虑利用二项式定理构造，发现当 $g_T=(-1)^{|T|-1}$ 时满足条件。

代码

点此查看代码

 #include <bits/stdc++.h>
using namespace std;
const int maxn=20,maxm=262200;
const int md=998244353,i2=499122177;
int n,m,i,j,u,v,b,f[maxm],g[maxm];
bool e[maxn][maxn];
int main(){
	scanf("%d%d",&n,&m); b=1<<n;
	for(i=1;i<=m;++i){
		scanf("%d%d",&u,&v);
		--u; --v; e[u][v]=e[v][u]=1;
	}
	memset(g,-1,sizeof(g));
	for(i=1;i<b;i<<=1) g[i]=0; f[0]=1;
	for(i=1;i<b;++i){
		if(g[i]){
			if(~g[v=i^(1<<(u=__lg(i&-i)))])
				for(;v;v^=j) if(e[u][__lg(j=v&-v)]) break;
			if(!v) g[i]=!g[i^(1<<u)];
		}
		for(j=i,v=0;j;j=(j-1)&i){
			if(~g[j]){
				u=f[i^j]; if(g[j]) u=md-u;
				v-=((v+=u)>=md)*md;
			}
		}
		f[i]=v;
	}
	printf("%d",1LL*f[b-1]*m%md*i2%md);
}

P5892 [IOI2014]holiday 假期

考虑最后能访问的城市一定在某个区间内，而在区间内一定会选择最大的若干个数（可以用主席树维护）。

考虑如何减少需要考虑的区间。令区间 $[l,r]$ 的答案为 $w(l,r)$ ，如果 $w(l_1,r_1)\ge w(l_1,r_2)$ 且 $r_1>r_2$ ，则对于 $\forall l_2\in(l_1,start]$ ， $[l_1,l_2)$ 内 $w(l_1,r_1)$ 对应的方案选择的数的集合不会覆盖 $w(l_1,r_2)$ 对应的方案（所以在 $w(l_1,r_1)\to w(l_2,r_1)$ 和 $w(l_1,r_2)\to w(l_2,r_2)$ 中前者减少的数不比后者多），而 $w(l_1,r_1)\to w(l_2,r_1)$ 能多选择的数的和多于 $w(l_1,r_2)\to w(l_2,r_2)$ （多选的数的数量一样，然而前者还没有选的数的数量更多），所以仍然有 $w(l_2,r_1)>w(l_2,r_2)$ 。此时左端点增加时最优右端点一定不会减小，可以直接决策单调性分治。

代码

点此查看代码

 #include <bits/stdc++.h>
using namespace std;
#define LL long long
const int maxn=100010;
const int maxm=3200010;
int n,s,d,i,l,r,m,x,p1,p2,tot;
int a[maxn],rt[maxn]; LL ans,sum[maxm]; 
int ls[maxm],rs[maxm],cnt[maxm];
void solve(int ll,int lr,int rl,int rr){
	if(ll>lr||rl>rr) return; int lm=(ll+lr)>>1;
	if(d<(s-lm)<<1){solve(lm+1,lr,rl,rr);return;} 
	int rk=min(rr,rl+d-((s-lm)<<1)),rm=rl; LL mx=0,nw;
	for(i=rl;i<=rk;++i){
		l=0; r=1e9; x=d-(i-lm)-(s-lm); 
		nw=0; p1=rt[i]; p2=rt[lm-1];
		if(cnt[p1]-cnt[p2]<=x) nw=sum[p1]-sum[p2];
		else{
			while(l<r){
				m=(l+r)>>1;
				if(cnt[rs[p1]]-cnt[rs[p2]]<=x){
					x-=cnt[rs[p1]]-cnt[rs[p2]];
					nw+=sum[rs[p1]]-sum[rs[p2]];
					r=m; p1=ls[p1]; p2=ls[p2];
				}
				else l=m+1,p1=rs[p1],p2=rs[p2];
			}
			nw+=1LL*l*min(x,cnt[p1]-cnt[p2]);
		}
		if(nw>mx) mx=nw,rm=i;
	}
	if(ans<mx) ans=mx; 
	solve(ll,lm-1,rl,rm); 
	solve(lm+1,lr,rm,rr);
}
void build(){
	l=0; r=1e9; x=a[i]; rt[i]=++tot; p1=rt[i-1];
	ls[tot]=ls[p1]; rs[tot]=rs[p1];
	sum[tot]=sum[p1]+x; cnt[tot]=cnt[p1]+1;
	while(l<r){
		m=(l+r)>>1;
		if(x<=m) p1=ls[tot],ls[tot]=tot+1,r=m; 
		else p1=rs[tot],rs[tot]=tot+1,l=m+1;
		rs[++tot]=rs[p1]; ls[tot]=ls[p1];
		sum[tot]=sum[p1]+x; cnt[tot]=cnt[p1]+1;
	}
}
int main(){
	scanf("%d%d%d",&n,&s,&d); ++s;
	for(i=1;i<=n;++i) scanf("%d",a+i),build(); 
	solve(max(1,s-(d<<1)),s,s,min(n,s+d)); reverse(a+1,a+n+1); 
	s=n-s+1; tot=0; for(i=1;i<=n;++i) build();
	solve(max(1,s-(d<<1)),s,s,min(n,s+d)); printf("%lld",ans);
	return 0;
}

posted @ 2023-02-03 17:29 Fran-Cen 阅读(64) 评论(0) 编辑收藏举报

刷新页面返回顶部

登录后才能查看或发表评论，立即登录或者逛逛博客园首页

相关博文：

· dp 优化部分例题

· 一/二月好题

· codeforces 基础思维题精选训练(1400 - 2100)

· dp题选做

· 2024 Noip 做题记录（八）

阅读排行：
· 分享一个免费、快速、无限量使用的满血 DeepSeek R1 模型，支持深度思考和联网搜索！
· 基于 Docker 搭建 FRP 内网穿透开源项目（很简单哒）
· ollama系列1：轻松3步本地部署deepseek，普通电脑可用
· 按钮权限的设计及实现
· 【杂谈】分布式事务——高大上的无用知识？

公告

昵称： Fran-Cen
园龄： 2年11个月
粉丝： 12
关注： 9

+加关注

2025年3月

日

一

二

三

四

五

六

Fran[CENSORED]Cwoi

dp 综合

P4187 [USACO18JAN]Stamp Painting G

代码

P7152 [USACO20DEC] Bovine Genetics G

代码

P3578 [POI2014]LAM-Solar lamps

代码

P6142 [USACO20FEB]Delegation P

代码

AT_joi2013ho5 バブルソート (Bubble Sort)

代码

P5244 [USACO19FEB] Mowing Mischief P

代码

P5156 [USACO18DEC]Sort It Out P

代码

CF1193A Amusement Park

代码

P5892 [IOI2014]holiday 假期

代码

公告

搜索

常用链接

最新随笔

随笔分类

随笔档案

CWOI

NOT CWOI

阅读排行榜

评论排行榜

推荐排行榜

最新评论

	#include <bits/stdc++.h>
	using namespace std;
	const int maxn=1000010;
	const int md=1000000007;
	int n,m,k,p,s,dp[maxn];
	inline int Pow(int d,int z){
	int r=1;
	do{
	if(z&1) r=(1LLrd)%md;
	d=(1LLdd)%md;
	}while(z>>=1);
	return r;
	}
	inline void Add(int &x,int y){x-=((x+=y)>=md)*md;}
	int main(){
	scanf("%d%d%d",&n,&m,&k);
	if(k==1){printf("%d",Pow(m,n));return 0;}
	dp[n]=s=m;
	for(p=n-1;p;--p){
	Add(s,dp[p]=(1LLs(m-1))%md);
	if(p+k-1<=n) Add(s,md-dp[p+k-1]);
	}
	printf("%d",(Pow(m,n)+md-s)%md);
	return 0;
	}

	#include <bits/stdc++.h>
	using namespace std;
	const int maxn=100010;
	const int md=1000000007;
	int i,j,k,p,c,n,dp[2][4][5][5];
	char s[maxn]; auto f=dp[0],g=dp[1];
	inline void Add(int &x,int y){x-=((x+=y)>=md)*md;}
	void chg(int c){
	for(j=0;j<4;++j)
	for(k=0;k<5;++k)
	Add(g[c][c][k],f[j][k][j]),
	Add(g[c][c][k],f[j][k][4]);
	if(i==1) return;
	for(j=0;j<4;++j) if(j!=c)
	for(k=0;k<4;++k)
	for(p=0;p<5;++p)
	Add(g[c][k][p],f[j][k][p]);
	}
	int main(){
	scanf("%s",s+1);
	n=strlen(s+1); f[0][4][0]=1;
	for(i=1;i<=n;++i){
	if((c=s[i])=='A') chg(0);
	else if(c=='C') chg(1);
	else if(c=='G') chg(2);
	else if(c=='T') chg(3);
	else for(c=0;c<4;++c) chg(c);
	swap(f,g); memset(g,0,sizeof(dp[0]));
	}
	for(j=c=0;j<4;++j)
	for(k=0;k<4;++k)
	Add(c,f[j][k][j]),
	Add(c,f[j][k][4]);
	printf("%d",c); return 0;
	}

	#include <bits/stdc++.h>
	using namespace std;
	#define ll long long
	const int maxn=200010;
	int n,i,a,b,c,d,x,y,pt,lt,rt,mt;
	int C[maxn],dp[maxn],lq[maxn],rq[maxn];
	ll lst; bool fl;
	struct Vals{
	ll val; int idx;
	inline bool operator <(const Vals &p)const{return val<p.val;}
	}A[maxn],B[maxn];
	struct node{
	int ra,rb,cnt,idx;
	inline bool operator <(const node &p)const{
	if(ra!=p.ra) return ra<p.ra;
	return rb<p.rb;
	}
	}N[maxn],LN[maxn],RN[maxn];
	inline void cmin(int &x,int y){if(x>y) x=y;}
	inline void Add(int p,int d){
	if(fl) C[p]+=d;
	else for(;p<=n;p+=p&-p) C[p]+=d;
	}
	inline int Query(int p){
	if(fl) return C[p];
	int r=0;
	for(;p;p^=(p&-p)) r+=C[p];
	return r;
	}
	void Solve(int L,int R,int l,int r){
	if(l>r) return;
	if(L==R){
	while(l<=r) dp[N[l++].idx]=L;
	return;
	}
	sort(N+l,N+r+1);
	int M=(L+R)>>1,lc=0,rc=0,m;
	for(i=l;i<=r;++i){
	if(N[i].idx<=M\|\|(a=Query(N[i].rb))>=N[i].cnt)
	Add(N[i].rb,1),LN[++lc]=N[i];
	else N[i].cnt-=a,RN[++rc]=N[i];
	}
	i=l; m=l+lc-1;
	while(lc) Add((N[i++]=LN[lc--]).rb,-1);
	while(rc) N[i++]=RN[rc--];
	Solve(L,M,l,m); Solve(M+1,R,m+1,r);
	}
	int main(){
	scanf("%d%d%d%d%d",&n,&a,&b,&c,&d);
	if(1LLad==1LLbc) fl=1,c=b,d=-a;
	if(1LLad<1LLbc) pt=-1; else pt=1;
	for(i=1;i<=n;++i){
	scanf("%d%d",&x,&y);
	N[i].idx=A[i].idx=B[i].idx=i;
	A[i].val=((1LLxd)-(1LLyc))*pt;
	B[i].val=((1LLya)-(1LLxb))*pt;
	}
	for(i=1;i<=n;++i) scanf("%d",&N[i].cnt);
	sort(A+1,A+n+1); sort(B+1,B+n+1);
	x=1; lst=A[1].val;
	for(i=1;i<=n;++i){
	while(A[i].val==lst&&i<=n) N[A[i++].idx].ra=x;
	if(i<=n) lst=A[i].val,N[A[i].idx].ra=++x;
	}
	x=1; lst=B[1].val;
	for(i=1;i<=n;++i){
	while(B[i].val==lst&&i<=n) N[B[i++].idx].rb=x;
	if(i<=n) lst=B[i].val,N[B[i].idx].rb=++x;
	}
	Solve(1,n,1,n);
	for(i=1;i<=n;++i) printf("%d ",dp[i]);
	return 0;
	}

	#include <bits/stdc++.h>
	using namespace std;
	const int maxn=20,maxm=262200;
	const int md=998244353,i2=499122177;
	int n,m,i,j,u,v,b,f[maxm],g[maxm];
	bool e[maxn][maxn];
	int main(){
	scanf("%d%d",&n,&m); b=1<<n;
	for(i=1;i<=m;++i){
	scanf("%d%d",&u,&v);
	--u; --v; e[u][v]=e[v][u]=1;
	}
	memset(g,-1,sizeof(g));
	for(i=1;i<b;i<<=1) g[i]=0; f[0]=1;
	for(i=1;i<b;++i){
	if(g[i]){
	if(~g[v=i^(1<<(u=__lg(i&-i)))])
	for(;v;v^=j) if(e[u][__lg(j=v&-v)]) break;
	if(!v) g[i]=!g[i^(1<<u)];
	}
	for(j=i,v=0;j;j=(j-1)&i){
	if(~g[j]){
	u=f[i^j]; if(g[j]) u=md-u;
	v-=((v+=u)>=md)*md;
	}
	}
	f[i]=v;
	}
	printf("%d",1LLf[b-1]m%md*i2%md);
	}