一/二月好题

AT_arc153_d Sum of Sum of Digits

考虑从低位到高位确定好 $x$ 的每一位。设第 $i$ 位之后部分对 $\sum f$ 的贡献已经定好，则在确认第 $i$ 位及之前的数位时，只需要考虑这一位对 $\sum f$ 的贡献，这一位的和只和之前多少个数进位到该位（显然将所有数按照后 $i-1$ 位排序后，进位的数一定是某个后缀的数），和这一位所填的数字有关。

代码

点此查看代码

#include <bits/stdc++.h>
using namespace std;
const int maxn=200010;
int n,i,j,k,u=1,s,d;
int a[maxn],b[maxn],f[maxn],c[10];
int dp[2][maxn],*X=dp[0],*Y=dp[1]; 
inline void cmin(int &x,int y){if(y<x) x=y;}
int main(){
	scanf("%d",&n);
	for(i=1;i<=n;++i) scanf("%d",a+i);
	memset(Y,0x3f,(n+1)<<2); Y[0]=0;
	for(i=1;i<=10;++i){
		swap(X,Y); memset(Y,0x3f,(n+1)<<2);
		for(j=1,s=d=0;j<=n;++j)
			s+=(f[j]=b[j]=(a[j]/u)%10);
		for(k=0;k<10;++k){ 
			for(j=0;j<=n;++j){
				cmin(Y[d],X[j]+s); 
				if(j==n) break;
				if(b[j+1]==9) s-=10,++d; 
				++s; ++b[j+1];
			}
		}
		for(j=1;j<=n;++j) ++c[f[j]];
		for(j=9;j;--j) c[j-1]+=c[j];
		for(j=n;j;--j) b[c[f[j]]--]=a[j];
		memcpy(a+1,b+1,n<<2); memset(c,0,40); u*=10;
	}
	printf("%d",Y[0]);
	return 0;
}

AT_arc153_e Deque Minimization

考虑不断在 $Y$ 的开头和结尾删除数字，并且保证依次删除的数的 $f$ 值刚好能对应当前的 $Y$。

先从比较简单的部分考虑起：设当前 $X$ 的某个前缀对应的 $f$ 值为 $Y$，$X$ 的新一位为 $u$，则 $Y$ 的第一位小于 $u$ 时 $u$ 一定放在队尾，大于 $u$ 时 $u$ 一定放在队首；此时 $Y$ 的某个前缀一定是单调不降的，所以 $Y$ 的第一位等于 $u$ 时 $u$ 放在队首一定不劣。（并且我们需要使得某个数不能在两种操作方式中被统计，所以必须放在队首）设 $dp_{l,d}$ 为满足 $X$ 的某个前缀操作成为了 $f(X)$ 的 $\{l,r\}$ 区间的 $X$，则转移有 $dp_{l,r}=[Y_l\le Y_{l+1}]dp_{l+1,r}+[Y_r>Y_l]dp_{l,r-1}$。

考虑有意义的初值只有 $dp_{i,i}$，最后只需要 $dp_{1,n}$，可以去掉不能转移到 $dp_{1,n}$ 的值。首先令 $Y$ 的最长不降前缀为 $Y_1\sim Y_{p-1}$，则一定有 $dp_p\sim dp_n$ 不能转移到 $dp_{1,n}$，且 $\forall i\in[2,p)$ 都有 $dp_i$ 能转移到 $dp_{i-1}$。考虑 $[Y_r>Y_l]dp_{l,r-1}$ 项如何优化转移。将 $dp_{l,r}$ 看成平面直角坐标系上的点 $(r,l)$，则转移方式如下图：

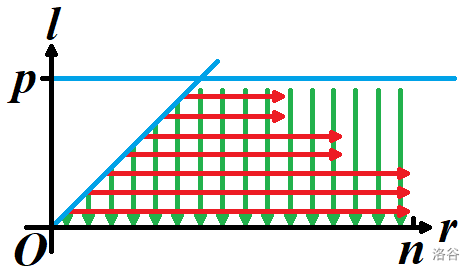
对于 $[1,p]$ 内的某个 $i$，令 $R_i$ 为最后一个满足 $Y_j>Y_i$ 的 $j$，显然有 $\forall k\in (i,R_i)$，$dp_{i,k-1}$ 能转移到 $dp_{i,k}$，且 $dp_{i,R_i-1}$ 不能转移到 $dp_{i,R_i}$。此时可能在 $[R_i,n]$ 内有 $dp_{i,r}\to dp_{i,r+1}$ 的转移，但是它们最终不会转移到 $dp_{1,n}$（可以把对应位置的 dp 值看成 $0$）。显然 $R$ 单调不增，且由于字符集大小只有 $9$，所以 $R$ 最多最会有 $9$ 个取值，可以分开对 $R$ 的每个取值，计算 $l$ 在边界时的 $dp_l$。

在从 $dp_{l_1}$ 转移到 $dp_{l_2}$ 时（且 $l_1,l_2$ 均为取到对应 $R$ 值的最小者），需要分开计算第二维在 $[l_1,n]$ 和在 $[l_2,l_1)$ 部分的贡献。对于前者，有 $dp_{l_2,k}\gets\sum_{j\le k}dp_{l_1,j}\binom{k-j+l_2-l_1}{l_2-l_1}$；对于后者，有 $dp_{l_2,k}\gets\sum_{l_2\le j\le \min(k,l_1-1)}\binom{k-l_2}{j-l_2}$。两者均可以 NTT 卷积计算。注意 $R$ 可能非法 / $l_1$ 可能非法，此时需要预处理这一部分的 dp 值（前者直接区间赋 $1$，后者只需要代入第二部分进行计算）。

代码（暂缺）

点此查看代码

AT_arc153_f Tri-Colored Paths

$\rm{From}$ $\rm{g}\color{red}{\rm{rass8woc}}$$.$

考虑将“用三种颜色染色”的方案数减去“用了三种颜色，然而不存在任何一条有三种颜色的路径”的方案数以得出答案。

考虑某个环有三种颜色的情况：
1. 环的大小 $\ge 4$。此时一定可以找出一条至少出现了两次的边，剩下的边可以组成一条路径且包含了三种颜色。
2. 该环为三元环（令这三个点为 $u,v,w$）。考虑其向其他点连的边的情况。
  1. 如果环上存在两个点 $u,v$ 均向其他点连边。如果 $u$ 和 $v$ 均连向了同一个点 $x$；则由路径 $x-u-w-v$ 和 $x-u-v-w$ 存在可得 $x-u$ 边颜色一定和 $v-w$ 相同，同理 $x-v$ 边的颜色一定和 $u-w$ 相同；此时 $x$ 不能向环外第二个点连边，$n=4$ 可以爆搜解决（同理可以爆搜 $n$ 更小的情况，方便之后的处理）。如果 $u$ 连向了 $x$，$v$ 连向了 $y$；则由于 $x-u-v-y$ 和 $x-u-w-v-y$ 可得 $x-u,v-y$ 选择任意一种颜色都会不合法。
  2. 否则环上只有一个点 $u$ 能和环外连边，此时环外面的边只能都和 $v-w$ 边同色。枚举 $v-w$ 边以找出所有这样的环的数量 $c$ 之后，其对方案数的贡献为 $6c$。
考虑某个环有两种颜色的情况（此时环上有三种颜色的方案可以直接视为非法）。此时一定存在第三种颜色的边 $u-v$，令 $u$ 可以不通过 $u-v$ 连向环上的某个点 $w$，$w$ 在环上相邻的点为 $x,y$；则 $w-x,w-y$ 中一定有一种颜色在环上出现了两次，去掉一条出现了两次的颜色的边之后一定会形成一条有三种颜色的路径。

综上，每个环只能有一种颜色，从而每个点双内部的边只能有一种颜色。考虑建出圆方树，则所有方点一定需要凑齐三种颜色，则一定存在某个圆点满足每个儿子的子树内的方点只有一种颜色，计算每个圆点的出边数量即可。

代码

点此查看代码

#include <bits/stdc++.h>
using namespace std;
const int maxn=200010;
const int md=998244353;
int n,m,i,j,u,v,w,a,t=1,tim,top;
int h[maxn],f[maxn],d[maxn],T[3];
int dfn[maxn],low[maxn],stk[maxn];
int p2[maxn],p3[maxn]; bool vis[maxn];
struct edge{int to,nxt;}E[maxn<<1];
bool dfs(int p){
	vis[p]=1; int lp,to;
	for(lp=h[p];lp;lp=E[lp].nxt){
		if(vis[to=E[lp].to]) continue;
		w+=(!(T[f[lp>>1]]++));
		if(w==3||dfs(to)) return 1;
		w-=(!(--T[f[lp>>1]]));
	}
	return vis[p]=0;
}
void color(int p){
	if(p>m){
		for(i=1,w=0;i<=n;++i){
			if(dfs(i)){
				memset(T,0,12);
				memset(vis+1,0,n);
				++a; break;
			}
		}
		return;
	}
	f[p]=0; color(p+1);
	f[p]=1; color(p+1);
	f[p]=2; color(p+1);
}
inline void Add(int &x,int y){x-=((x+=y)>=md)*md;}
void tarjan(int p){
	dfn[p]=low[p]=++tim;
	stk[++top]=p; int lp,to;
	for(lp=h[p];lp;lp=E[lp].nxt){
		to=E[lp].to;
		if(!dfn[to]){
			tarjan(to);
			if(low[to]==dfn[p]){
				for(u=0;u!=p;++f[u=stk[top--]]);
				stk[++top]=p;
			}
			else low[p]=min(low[p],low[to]);
		}
		else low[p]=min(low[p],dfn[to]);
	}
}
int main(){
	p2[0]=p3[0]=1;
	for(i=1;i<maxn;++i){
		Add(p2[i]=p2[i-1],p2[i-1]);
		p3[i]=(3LL*p3[i-1])%md;
	}
	scanf("%d%d",&n,&m);
	for(i=1;i<=m;++i){
		scanf("%d%d",&u,&v); 
		++d[u]; ++d[v];
		E[++t]={v,h[u]}; h[u]=t;
		E[++t]={u,h[v]}; h[v]=t;
	}
	if(n<=5){
		color(1);
		printf("%d\n",a);
		return 0;
	}
	a=((p3[m]+3-3LL*p2[m])%md+md)%md;
	for(i=2;i<=t;i+=2){
		u=E[i].to; v=E[i|1].to;
		if(d[u]==2&&d[v]==2){
			if(E[j=h[u]].to==v) j=E[j].nxt; w=E[j].to; 
			if(E[j=h[v]].to==u) j=E[j].nxt; if(w==E[j].to) Add(a,md-6);
		}
	} 
	tarjan(1);
	for(i=1;i<=n;++i)
		Add(a,((3LL*p2[f[i]]-p3[f[i]]-3)%md+md)%md);
	printf("%d\n",a);
	return 0;
}

CF1775F Laboratory on Pluto

考虑最优方案中，整个多边形的周长一定可以向外拓展成一个矩形的形状。证明考虑不断将一部分矩形向右/向下移（在不增加原周长的情况下）计数时可以从周长相等，面积最大的矩形开始枚举；在每个矩形对应的四个角上分别删掉阶梯形的一部分即可。显然每个矩形需要用到的对应下标所有的方案一定有四个地方的阶梯形不会重合（否则对应的多边形一定可以周长更小），所以可以将对应阶梯形的构造方案分别用 dp 求出来然后卷积即可（项数不大），每个 $n$ 对应的方案就是其能对应的矩形的删除部分的 dp 值之和。

代码

点此查看代码

#include <bits/stdc++.h>
using namespace std;
const int maxs=650;
const int maxn=400010;
int t,u,i,j,k,a,b,c,d,m;
int ce[maxn],ans[maxn];
int s[maxs][maxs],f[maxs],g[maxs];
inline void Add(int &x,int y){x-=((x+=y)>=m)*m;}
int main(){
	for(i=1,a=2;i<maxn;++i){
		if((a>>1)*(a-(a>>1))<i) ++a;
		ce[i]=a;
	}
	scanf("%d%d",&t,&u);
	if(u==2){
		f[0]=f[1]=1; scanf("%d",&m);
		for(i=1;i<maxs;++i)
			for(j=i;j<maxs;++j)
				s[i][j]=1;
		for(i=2;i<maxs;++i){
			for(j=1;j<i;++j)
				Add(s[i][j]=s[i][j-1],s[i-j][j]);
			Add(s[i][i],s[i][i-1]); f[i]=s[i][i];
			for(j=i+1;j<maxs;++j) s[i][j]=s[i][j-1];
		}
		memcpy(g,f,sizeof(f));
		for(i=0;i<3;++i)
			for(j=maxs-1;~j;g[j--]=a)
				for(k=a=0;k<=j;++k)
					a=(1LL*f[k]*g[j-k]+a)%m;
		for(i=1,d=2;i<maxn;++i){
			u=ce[i]; a=0;
			for(b=u>>1;;--b){
				if((c=b*(u-b))<i) break;
				Add(a,g[c-i]);
			}
			for(b=(u>>1)+1;;++b){
				if((c=b*(u-b))<i) break;
				Add(a,g[c-i]);
			}
			ans[i]=a; 
		}
		while(t--){
			scanf("%d",&a);
			printf("%d %d\n",ce[a]<<1,ans[a]);
		}
	}
	else{
		while(t--){
			scanf("%d",&a);
			c=ce[a]>>1; b=ce[a]-c;
			printf("%d %d\n",c,b);
			for(i=1;i<=c;++i){
				for(j=1;j<=b;++j){
					if(a) putchar('#'),--a;
					else putchar('.');
				}
				putchar('\n');
			}
		}
	}
}

CF1783G Weighed Tree Radius

考虑在原树上每个点 $i$ 都接两条长度为 $a_i$ 的边，分别接到新的点 $n+i,2n+i$ 上，则问题变成了求 $1\sim n$ 点中每个点到其他点的路径长度最大值的最小值。考虑所有 $a_i$ 均为 $0$ 时，这个问题的答案即为 $\lceil\frac{直径}2\rceil$（考虑从每个点到直径上某个点的距离和直径上该点到直径端点的距离）。然后考虑新树上的直径一定是某个 $a_u+d_v(u)+a_v$ 的形式，且 $a_u,a_v<\frac 12(a_u+d_v(u)+a_v)$；所以令新树的直径为 $D$，则每个点到其他点路径长度最大值不小于 $\lceil\frac D2\rceil$，且 $1\sim n$ 内一定有一个点能取到这个值。问题就成为了在一棵树上动态修改边权然后查询直径。

动态查询直径时，先考虑将问题转化为区间问题，欧拉序上两个点 $x,y$ 的 $\rm{lca}$ 为 $dfn_x\sim dfn_y$ 内深度最小的点 $z$，所以对应的直径为区间两端减区间最小值的两倍。然后考虑在线段树上如何合并两个区间内的信息：可以把 $dep_x+dep_y-2dep_{\rm{lca}}$ 拆成 $(dep_x-2dep_{\rm{lca}})+dep_y$ 或 $(dep_y-2dep_{\rm{lca}})+dep_x$ 分别计算。合并信息时，如果 $x,y$ 在不同区间，则需要取左端的 $(dep_x-2dep_{\rm{lca}})$ 或右端的 $(dep_y-2dep_{\rm{lca}})$。同时由于每次修改的都是叶节点的 $\rm{lca}$，只会在欧拉序上出现一次，所以每次单点改全局查即可。

代码

点此查看代码

#include <bits/stdc++.h>
using namespace std;
const int maxn=200010;
int n,q,i,u,v,a,t,h[maxn*3],to[maxn*3];
int dep[maxn*3],dfn[maxn*3],rnk[maxn*6];
struct edge{int to,ed,nxt;}E[maxn*4];
void dfs(int p,int f,int d){
	dep[p]=d; rnk[++t]=p; dfn[p]=t;
	for(int to,lp=h[p];lp;lp=E[lp].nxt){
		to=E[lp].to; if(to==f) continue;
		dfs(to,p,d+E[lp].ed); rnk[++t]=p;
	}
}
struct node{int mx,mn,lx,rx,lr;}tr[maxn*24];
#define ls(p) p<<1
#define rs(p) p<<1|1
#define mx(p) tr[p].mx
#define mn(p) tr[p].mn
#define lx(p) tr[p].lx
#define rx(p) tr[p].rx
#define lr(p) tr[p].lr
inline void pushup(int p){
	lx(p)=max(max(lx(ls(p)),lx(rs(p))),
				  mx(ls(p))+mn(rs(p)));
	rx(p)=max(max(rx(ls(p)),rx(rs(p))),
				  mx(rs(p))+mn(ls(p)));
	lr(p)=max(max(lr(ls(p)),lr(rs(p))),
			  max(lx(ls(p))+mx(rs(p)),
				  mx(ls(p))+rx(rs(p))));
		mx(p)=max(mx(ls(p)),mx(rs(p))); 
		mn(p)=max(mn(ls(p)),mn(rs(p)));
}
void build(int p,int l,int r){
	if(l==r){
		int x=rnk[l]; to[x]=p;
		tr[p]={dep[x],-(dep[x]<<1),0,0,0};
		return;
	}
	int m=(l+r)>>1;
	build(ls(p),l,m);
	build(rs(p),m+1,r);
	pushup(p);
}
int main(){
	scanf("%d",&n); 
	for(i=1;i<=n;++i){
		scanf("%d",&a);
		E[++t]={i+n,a,h[i]}; h[i]=t;
		E[++t]={i+n+n,a,h[i]}; h[i]=t;
	}
	for(i=1;i<n;++i){
		scanf("%d%d",&u,&v);
		E[++t]={v,1,h[u]}; h[u]=t;
		E[++t]={u,1,h[v]}; h[v]=t;
	}
	dfs(1,0,t=0); build(1,1,t); scanf("%d",&q);
	while(q--){
		scanf("%d%d",&u,&v); a=dep[u]+v;
		tr[t=to[n+u]]={a,-(a<<1),0,0,0};
		while(t>>=1) pushup(t);
		tr[t=to[n+n+u]]={a,-(a<<1),0,0,0};
		while(t>>=1) pushup(t);
		printf("%d\n",(lr(1)+1)>>1);
	}
	return 0;
}

AT_arc154_d A + B > C ?

一个不优秀的做法。

注意到可以询问 $(i,i,j)$ 以得出 $2i$ 和 $j$ 之间的大小关系。我们可以通过询问 $\forall i,(1,1,i)$，这样可以得出所有 $\le \frac {P_1}2$ 的数（或者是得出 $P_1=1$）。然后在 $\le \frac{P_1}2$ 的数内再次寻找知道找到 $1$ 所在的位置。由于每次询问对应序列长度一定至少减半，所以这部分询问次数不超过 $2n$。这个时候询问 $P_i+1>P_j$ 是否成立等效于询问 $P_i\ge P_j$ 是否成立；而 $P_i\ne P_j$ 所以这次操作直接等效于询问 $P_i>P_j$ 是否成立。然后就可以使用某些比较次数不超过 $n\log_2 n$ 的排序算法过掉本题。（因为试图考虑如何得出 $P_i$ 的具体值而被误导了很久）（注意内省排序 sort 极端情况下会 $\log_2 n$ 遍遍历整个数组才会转成堆排序，询问次数会超限，所以可以使用 stable_sort 或手写归并）（归并不会跑满 $n\log_2 n$，所以过了）

~~听说 ${\rm Z}{\color{red}{\rm{MJ}}}$ 奆佬在 5 分钟内切掉还自认为很正常，学不来学不来。~~

代码

点此查看代码

#include <bits/stdc++.h>
using namespace std;
const int maxn=2010;
int n,i,d,u,t,c[maxn],p[maxn]; char s[5];
inline bool cmp(const int &x,const int &y){
	printf("? %d %d %d\n",x,u,y);
	fflush(stdout); scanf("%s",s+1);
	return s[1]=='N';
}
int main(){
	scanf("%d",&n);
	for(i=1;i<=n;++i) p[i]=i;
	for(d=n;u=p[1],d!=1;){
		t=0;
		for(i=2;i<=d;++i){
			printf("? %d %d %d\n",p[i],p[i],u);
			fflush(stdout); scanf("%s",s+1);
			if(s[1]=='N') c[++t]=i;
		}
		if(!t) break; d=t;
		for(i=1;i<=t;++i) p[i]=p[c[i]];
	}
	for(i=d=1;i<=n;++i) if(i!=u) p[++d]=i;
	stable_sort(p+2,p+n+1,cmp); 
	for(i=1;i<=n;++i) c[p[i]]=i; printf("! "); 
	for(i=1;i<=n;++i) printf("%d ",c[i]);
}

AT_arc155_d Avoid Coprime Game

$\rm{From}$ $\rm{S}{\color{red}{\rm{qrtSecond}}}$$.$

考虑如何使用尽量少的信息维护某个局面下留下的 $a_i$。显然对于任意一个 $G$，没有因数 $G$ 的数一定会保留下来；所以维护一个 $\{G,i\}$（其中 $i$ 表示当前剩余的有因数 $G$ 的数的个数）就可以实现维护完整的状态和转移。

考虑简化对应的状态，看能否单独从 $G$ 的状态判断先手/后手必胜。令 $dp_{G,j}$ 表示对于某个 $G$，轮到玩家 $j$ 时 $j$ 有无必胜策略。转移时枚举所有 $a_i$，如果某个 $a_i$ 满足 $1<\gcd(a_i,G)<G$，则可以从 $dp_{\gcd(a_i,G),!j}$ 转移到 $dp_{G,j}$。同时对于某个 $dp_{G,j}$，如果所有的 $dp_{\gcd(a_i,G),!j}$ 均为 $1$，则 $j$ 必须考虑能否选择一个为 $G$ 的倍数的数。然而如果当前的是 $G$ 的倍数的数为偶数，则该玩家在选择 $G$ 的倍数后对手也可以选择 $G$ 的倍数，最终 $j$ 必须选择一个不是 $G$ 的倍数的数，无法改变局势；否则在轮到对手时需要对手对应的 $dp_{G,!j}=0$ 才存在 $j$ 的必胜策略。

考虑优化对应的转移。令 $c_{G,d}=\sum_{i=1}^n[\gcd(a_i,G)=d]$，则 $\sum_{i\ge 1}c_{G,id}=\sum_{i=1}^n[a_i\bmod d=0]$。可以对于某个 $G$，降序枚举 $G$ 的所有因数，然后对于每个因数枚举其所有倍数以得出对应的 $c_G$。

代码

点此查看代码

#include <bits/stdc++.h>
using namespace std;
const int maxn=200010;
int n,m,i,j,a[maxn],f[maxn],b[maxn],c[maxn];
bool dp[maxn][2]; vector<int> v[maxn];
int main(){
	scanf("%d",&n);
	for(i=1;i<=n;++i){
		scanf("%d",a+i);
		++f[a[i]]; m=max(m,a[i]);
	}
	for(i=m;i>1;--i){
		for(j=i;j<=m;j+=i){
			v[j].push_back(i);
			b[i]+=f[j];
		}
	}
	for(i=2;i<=m;++i){
		for(int j:v[i]){
			c[j]=b[j]; if(i==j) continue;
			for(int k:v[i/j]) c[j]-=c[j*k];
			if(!c[j]) continue;
			dp[i][0]|=!dp[j][1];
			dp[i][1]|=!dp[j][0]; 
		}
		if(b[i]&1) dp[i][0]|=!dp[i][1];
		else dp[i][1]|=!dp[i][0];
	}
	for(i=1;i<=n;++i){
		if(dp[a[i]][1]) printf("Aoki\n");
		else printf("Takahashi\n");
	}
	return 0;
}

AT_arc155_e Split and Square

考虑 $S$ 内的线性基。设 $\{e_1,e_2,e_3,\cdots,e_n\}$ 为原集合 $S$ 的线性基（且这些数均在 $S$ 内出现过），则在将 $S$ 分成 $T_1,T_2$ 之后，令 $\{e_1,e_2,\cdots,e_m\}$ 被分到了 $T_1$，$\{e_{m+1},e_{m+2},\cdots,e_n\}$ 被分到了 $T_2$，则由线性基定义可得 $\{e_1\oplus e_i|i\in[2,m]\}\cup\{e_n\oplus e_i|i\in[m+1,n-1]\}$ 内的数两两不能互相表出，所以线性基大小最多减少 $2$。而如果 $S$ 内存在 $0$，则 $0$ 被分到任意一个集合都会保留集合内的所有数包括 $0$ 本身，故此时一次操作后线性基大小最多减少 $1$。

考虑能否在每一次操作中都让线性基大小减少 $1$ 或 $2$。在让线性基大小减少 $1$ 时，可以将需要通过 $e_1$ 表出的数放在 $T_1$，其他数（和可能存在的 $0$）放在 $T_2$；则 $f(T_1)$ 内的所有数的 $e_1$ 部分都会被消掉，线性基大小减少了 $1$。考虑 $\{e_1\oplus e_i|i\in[2,m]\}\cup\{e_n\oplus e_i|i\in[m+1,n-1]\}$ 可以表出的数，显然它们可以表出所有的，满足在 $e_1\sim e_m$ 内选择偶数个数，$e_{m+1}\sim e_n$ 内选择偶数个数能表出的数，总共 $2^{n-2}$ 个数。如果需要使得线性基大小减小 $2$，则我们需要 $f(T_1)\cup f(T_2)$ 只能表出这么多的数。此时如果 $T_1$ 内存在某个数满足在 $e_1\sim e_m$ 内选择偶数个数能表出的数，则 $f(T_1)$ 内的数能表出的数就会包括在 $e_1\sim e_m$ 内选择奇数个数能表出的数，不符合题意。所以需要在 $T_1$ 内放且只放能用能在 $e_1\sim e_m$ 内选择奇数个数，$e_{m+1}\sim e_n$ 内选择偶数个数能表出的数，在 $T_2$ 内放且只放能用在 $e_1\sim e_m$ 内选择偶数个数，$e_{m+1}\sim e_n$ 内选择奇数个数能表出的数；综合起来就是 $S$ 内所有数都能被线性基内奇数个数表出。

代码

点此查看代码

#include <bits/stdc++.h>
using namespace std;
const int maxn=310;
int n,m,i,j,t; bool f;
bitset<maxn> b[maxn],c[maxn],x,v;
int main(){
	scanf("%d%d",&n,&m); 
	for(i=1;i<=n;++i){
		cin>>x; v.reset(); 
		v[i]=1; f|=x.none();
		if(n==1){
			printf("%d",x.any());
			return 0;
		}
		for(j=m-1;~j;--j){
			if(!x[j]) continue;
			if(b[j].none()){
				b[j]=x; c[j]=v;
				++t; break;
			}
			x^=b[j]; v^=c[j];
		}
		f|=(j<0&&(v.count()&1));
	}
	printf("%d",t-!f); return 0;
}

CF1787H Codeforces Scoreboard

先加上 $\sum a_i$ 部分。考虑最后取 $b_i-k_it_i$ 部分的题目一定是按照 $k_i$ 降序进行选择的，将所有题目按照 $k_i$ 降序排序后，则问题变成了在所有题目中选择一个子序列，使得子序列的 $\sum((b_i-a_i)-k_it_i)$ 最大（显然 $b_i-a_i-k_it_i\le 0$ 时该决策会被替换掉，所以可以不单独讨论这种情况）。

考虑其差分数组的性质。此时 $$

代码

点此查看代码

[AGC061A] Long Shuffle

考虑进行 shuffle(1,2n) 后，一定有且只有某些 $a_{2i-1},a_{2i}$ 互换。

证明：考虑将 shuffle(1,2n) 拆成 shuffle(1,2n-2)、shuffle(2,2n-1)、shuffle(2,2n-1)、shuffle(3,2n)。考虑归纳，设 shuffle(1,2n-2) 时只会对某些 $a_{2i-1},a_{2i}$ 互换，则中间两个 shuffle(2,2n-1) 可以抵消，而 shuffle(1,2n-2) 和 shuffle(3,2n) 均只会将某些 $a_{2i-1},a_{2i}$ 互换；且 n=1 时只会交换 $a_1,a_2$；所以该命题成立。

此时设 $P_{i,j}$ 为 shuffle(1,2i) 时 $a_{2j-1}$ 和 $a_{2j}$ 是否互换，则有 $P_{i,j}=P_{i-1,j}\oplus P_{i-1,j-1}$（非法 $P$ 值可以设为 $0$），初值有 $P_{1,1}=1$。此时可以发现递推方式类似组合数（其实 $P_{i,j}$ 就是组合数 $\binom{i-1}{j-1}\bmod 2$），就很好处理了。然后 $n$ 为奇数时可以拆成 shuffle(1,n-1) 和 shuffle(2,n) 也很好处理。

代码

点此查看代码

#include <bits/stdc++.h>
using namespace std;
#define ll long long
int t; ll n,k,a;
inline bool P(ll i,ll j){
	ll si=0,sj=0,k=i-j;
	while(i>>=1) si+=i;
	while(j>>=1) sj+=j;
	while(k>>=1) sj+=k;
	return si==sj;
}
inline ll S(ll i,ll j){
	return ((j-1)^P((i-1)>>1,(j-1)>>1))+1;
}
int main(){
	scanf("%d",&t);
	while(t--){
		scanf("%lld%lld",&n,&k);
		if(n&1){
			if(k!=n) a=S(n-1,k);
			if(k!=1&&S(n-1,k-1)!=k-1){
				if((k^=1)!=n) a=S(n-1,k);
				else a=n;
			}
		}
		else a=S(n,k); printf("%lld\n",a);
	}
	return 0;
}

[AGC061B] Summation By Construction

代码

点此查看代码

[AGC061C] First Come First Serve

代码

点此查看代码

[AGC061D] Almost Multiplication Table

代码

点此查看代码

[ABC289Ex] Trio

考虑在所有方案中容斥掉在 $T$ 秒之前三人相遇的方案，此时令 $f_i$ 为三人从起点出发经过 $i$ 秒在同一个点 第一次 相遇的方案数，$g_i$ 为三人从同一个点开始出发经过 $i$ 秒走到另一个点的方案数，$h_i$ 为三人从起点出发经过 $i$ 秒走到某个点的方案数；则有 $f_i=h_i-\sum_{j=0}^{i-1}f_jg_{i-j}$。可以分治 FFT 求。此时问题在如何求 $g,h$。

考虑求某个 $h_i$ 严格强于 $g_i$。此时枚举终点 $j$ 有 $h_i=\sum_j\binom i{\frac{a-j+i}{2}}\binom i{\frac{b-j+i}{2}}\binom i{\frac{c-j+i}{2}}$，换元可得 $h_i=\sum_{j=0}^i\binom ij\binom{i}{j+\frac{b-a}2}\binom{i}{j+\frac{c-a}2}$，然后将组合数拆开可得 $h_i=(i!)^3\times\sum_{j=0}^i\frac 1{j!(j+\frac{b-a}2)!(j+\frac{c-a}2)!}\times\frac 1{(i-j)!((i-j)-\frac{b-a}2)!((i-j)-\frac{c-a}2)!}$，卷积计算即可。

代码

点此查看代码

#include <bits/stdc++.h>
using namespace std;
const int maxn=100010;
const int maxb=262150;
const int md=998244353,_g=3;
int a,b,c,T,t,p,i,j,k,u,v,le;
int F[maxb],G[maxb],r[maxb];
int fac[maxn],inv[maxn],f[maxn],g[maxn],h[maxn];
inline int Pow(int d,int z){
	int r=1;
	do{
		if(z&1) r=1LL*r*d%md;
		d=1LL*d*d%md;
	}while(z>>=1); return r;
}
inline void Add(int &x,int y){x-=((x+=y)>=md)*md;}
void dft(int *f){
	for(i=1;i<t;++i) if(i<r[i]) swap(f[i],f[r[i]]);
	for(i=1,le=2;le<=t;i=le,le<<=1){
		for(j=0,v=Pow(_g,(md-1)/le);j<t;j+=le){
			for(k=0,u=1;k<i;++k,u=1LL*u*v%md){
				p=1LL*f[i+j+k]*u%md;
				Add(f[i+j+k]=f[j+k],md-p); 
				Add(f[j+k],p);
			}
		}
	}
}
inline void Mul(){
	for(i=1;i<t;++i) r[i]=(r[i>>1]>>1)|((i&1)*(t>>1));
	dft(F); dft(G); for(i=0;i<t;++i) F[i]=1LL*F[i]*G[i]%md;
	dft(F); reverse(F+1,F+t); p=Pow(t,md-2);
}
void Solve(int l,int r){
	if(l==r){Add(f[l]=md-f[l],h[l]);return;}
	int m=(l+r)>>1; Solve(l,m); 
	for(t=1,a=m-l+r-l-1;t<=a;t<<=1); 
	memset(F,0,t<<2); memset(G,0,t<<2);
	memcpy(F,f+l,(m-l+1)<<2); memcpy(G,g+1,(r-l)<<2); Mul(); 
	for(i=m+1;i<=r;++i) Add(f[i],1LL*F[i-l-1]*p%md); Solve(m+1,r);
}
int main(){
	for(i=fac[0]=1;i<maxn;++i) fac[i]=1LL*fac[i-1]*i%md;
	inv[maxn-1]=Pow(fac[maxn-1],md-2);
	for(i=maxn-1;i;--i) inv[i-1]=1LL*inv[i]*i%md;
	scanf("%d%d%d%d",&a,&b,&c,&T); b=(b-a)/2; c=(c-a)/2;
	for(i=0;i<=T;++i){
		if(i+b>=0&&i+c>=0) F[i]=1LL*inv[i]*inv[i+b]%md*inv[i+c]%md;
		if(i-b>=0&&i-c>=0) G[i]=1LL*inv[i]*inv[i-b]%md*inv[i-c]%md; 
	}
	for(t=1,T<<=1;t<=T;t<<=1); 
	for(Mul(),i=0,T>>=1;i<=T;++i){
		F[i]=1LL*F[i]*p%md*fac[i]%md;
		h[i]=1LL*fac[i]*fac[i]%md*F[i]%md;
	}
	memset(F,0,t<<2); memset(G,0,t<<2);
	for(i=0;i<=T;++i) F[i]=G[i]=1LL*inv[i]*inv[i]%md*inv[i]%md; 
	for(Mul(),i=0;i<=T;++i){
		F[i]=1LL*F[i]*p%md*fac[i]%md;
		g[i]=1LL*fac[i]*fac[i]%md*F[i]%md;
	}
	Solve(0,T); p=Pow(8,md-1-T); 
	printf("%d",1LL*f[T]*p%md); return 0;
}

posted @ 2023-01-31 10:09 Fran-Cen 阅读(48) 评论(0) 编辑收藏举报

刷新页面返回顶部

Fran[CENSORED]Cwoi

一/二月好题

AT_arc153_d Sum of Sum of Digits

代码

AT_arc153_e Deque Minimization

代码（暂缺）

AT_arc153_f Tri-Colored Paths

代码

CF1775F Laboratory on Pluto

代码

CF1783G Weighed Tree Radius

代码

AT_arc154_d A + B > C ?

代码

AT_arc155_d Avoid Coprime Game

代码

AT_arc155_e Split and Square

代码

CF1787H Codeforces Scoreboard

代码

[AGC061A] Long Shuffle

代码

[AGC061B] Summation By Construction

代码

[AGC061C] First Come First Serve

代码

[AGC061D] Almost Multiplication Table

代码

[ABC289Ex] Trio

代码

公告