CF/AT 题目整理

话说我有多长时间没去做 CF/AT 题目了（）记录考试中途想了但是没有完全想的，可能会在将来想的题

可能不保证质量，因为众所周知，Fran_Cen 能场切的题目的难度区间很是令人捉摸不透（低而且捉摸不透），所以这里可能是某种意义上的低级错误集。（~~指被 *1500 甚至 *800 吊打~~）

下面空着的题目的解法是朦胧的，没有空着的题目的解法是顺势朦胧的。

可以看成 【亿些防不住 AK 的水题】 A.G. Version（After GaryH）。

CF1707C Dfs Trees

首先图上的每条边边权唯一，对应了图的 MST 唯一。然后在某个点开始 dfs 时，非树边一定会是树上的返祖边，所以如果以某个点为 MST 的根时出现了横叉边，则该点的 dfs 树一定不会是 MST，否则由于 dfs 的顺序，非树边一定会是返祖边。此时直接对每条非树边将其连接的子树根节点加一即可。

具体实现时，非树边为横叉边时可以直接树上差分，而非树边是返祖边时（设该边为 \((u,v)\) 且 \(u\) 是 \(v\) 的祖先）需要将 \(v\) 跳祖先到 \(u\) 的某个儿子 \(w\) 处，然后将根节点和 \(v\) 的差分加一，将 \(w\) 的差分减一。

CF1707D Partial Virtual Trees

CF1707E Replace

题意

有一个长为 \(n\) 的数组 \(a\)。定义 \(F_k(\{l,r\})=\begin{cases}F_1(F_{k-1}(\{l,r\}))&k>1\\\left\{\min\limits_{i=l}^r a_i,\max\limits_{i=l}^r a_i\right\}&k=1\\\{l,r\}&k=0\end{cases}\)

现在有 \(q\) 次询问，第 \(i\) 次询问给定 \(l_i,r_i\)，求满足 \(F_k(\{l_i,r_i\})=\{1,n\}\) 的最小 \(k\)，不存在则输出 \(-1\)。\(1\le a_i\le n\le 10^5\)。

解法

令 \(\{l_1,r_1\}\oplus\{l_2,r_2\}=\{\min(l_1,l_2),\max(r_1,r_2)\}\)。

此时可以发现一个性质（可能是一个很不显然的性质）：\(\forall k,l_1,r_1,l_2,r_2,\) 如果 \([l_1,r_1]\cup[l_2,r_2]\ne \O\)，则 \(F_k(\{l_1,r_1\})\oplus F_k(\{l_2,r_2\})=F_k(\{l_1,r_1\}\oplus\{l_2,r_2\})\)。

证明：对于 \(k=1\) 的情况显然成立，且 \(F_1(\{l_1,r_1\}),F_1(\{l_2,r_2\})\) 有交。考虑归纳，设对于 \(0\sim k-1\) 上述性质成立，则 \(F_k(\{l_1,r_1\})\oplus F_k(\{l_2,r_2\})=F_1(F_{k-1}(\{l_1,r_1\}))\oplus F_1(F_{k-1}(\{l_2,r_2\}))=F_1(F_{k-1}(\{l_1,r_1\})\oplus F_{k-1}(\{l_2,r_2\}))=F_1(F_{k-1}(\{l_1,r_1\}\oplus\{l_2,r_2\}))=F_k(\{l_1,r_1\}\oplus\{l_2,r_2\})\)。

故可以考虑倍增，设 \(f_{i,j,k}\) 为 \(F_{2^k}(\{i,i+2^j-1\})\)，则转移时有 \(f_{i,j+1,k}=f_{i,j,k}\cup f_{i+2^j,j,k}\)，\(f_{i,j,k+1}\) 可以使用 st 表拆区间的方法求。

然后如果某个查询的 \(k\ne 0\)，则一定有 \(F_1(\{1,n\})=\{1,n\}\)；可以直接用 st 表的类似方式倍增出对应的 \(k\) 即可。如果求到的 \(k\) 大于合法区间个数 \(\frac 12n(n-1)\) 则直接判为无解。

p.s. 考虑 \(F_k(\{i,i\})\) 的情况。此时可以把它赋为 \(\{n,1\}\)（\(\forall l,r\in[1,n],l\le r,\{l,r\}\oplus\{n,1\}=\{l,r\}\)，同时 \(\forall l,r\in[1,n],[l,r]\cup [i,i]\ne \O,[l,r]\oplus[i,i]=[l,r]\)），表示空区间。同时 \(\forall n>1,k,F_k(\{i,i\})\ne \{1,n\}\)，可以直接特判该情况。

代码

CF1721F Matching Reduction

考虑二分图中最大匹配 = 最小点覆盖大小的性质。显然删去一个点之后最大匹配大小最多会减少 \(1\)（如果其为最大匹配必经点），而删去最小点覆盖之后整个图只会剩下最大独立集，此时最大匹配大小为 \(0\)；所以每次删去最小点覆盖内的一个点一定满足题意。

此时我们需求最小点覆盖和最大独立集之间的最大匹配。然而求得的最大匹配一定就是最小点覆盖和最大独立集之间的最大匹配，因为匹配中每条边至少有一个端点在最小点覆盖内，而最小点覆盖大小即为最大匹配大小；所以直接依次删去原最大匹配的边即可。

代码

CF1730D Prefixes and Suffixes

考虑某两个字符 \(s_i\) 和 \(t_{n+1-i}\) 在某些操作后的变化。如果某此次操作的 \(k<i\)，则 \(s_i\) 和 \(t_{n-i}\) 仍然不变；否则 \(s_i\) 会变成 \(t_{n-k+i}\)，\(t_{n+1-i}\) 会变成 \(s_{k-i}\)，仍然满足两者下标之和为 \(n+1\)。同时可以通过下面的步骤使得某对 \(s_i\) 和 \(t_{n+1-i}\) 分别处于 \(s_1\) 和 \(t_n\) 的位置且不会改变其他字母的相对顺序：

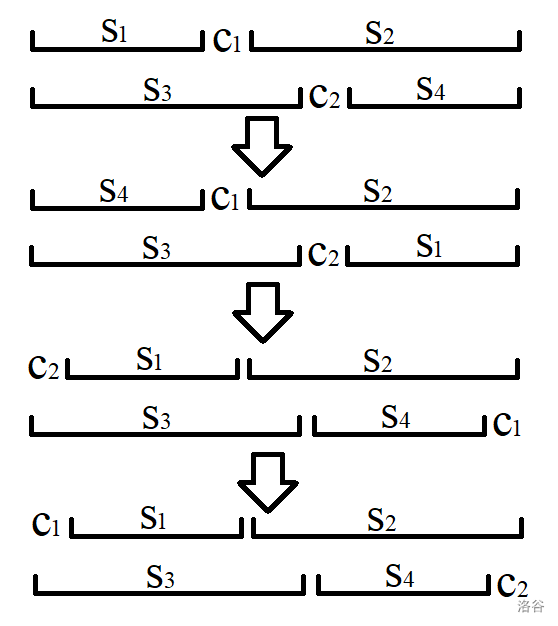
此时可以处理出每对无序二元组 \(\{s_i,t_{n+1-i}\}\)，然后看其能否排成一个回文串即可（能排成回文串则某个字母一定可以对应回文位置的字母），如果长度为奇数则需要回文中心 \(s_i=t_{n+1-i}\)。

代码

CF1730E Maximums and Minimums

代码

CF1730F Almost Sorted

代码

CF1737D Ela and the Wiring Wizard

考虑在某个图上可以如何调整最短路使得代价 + 最短路更短。考虑 \(1\sim n\) 的路径上的两条相邻的边 \(w_1,w_2\)。

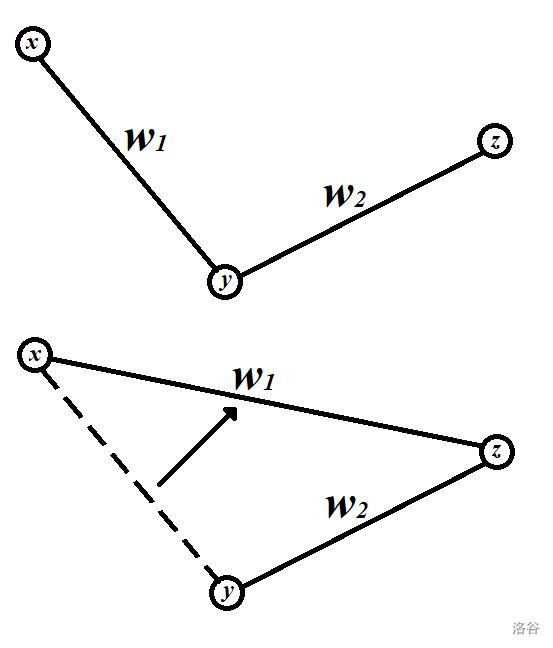
如果 \(w_2\ge w_1\)，显然可以将 \(w_1\) 进行调整使得代价 + 最短路更短。最后路径上只会有原来最短的一条边，以单独的一条边作为整个路径一定不劣。

然后考虑如何将某条边移动到 \(1\sim n\) 位置。此时可以只用改变这条边而不改变其他边。

假设某部分操作需要 \(w_2\) 连接 \(x,y\)。不移动 \(w_1\)，将会产生 \(2w_2\) 的代价（可以走自己，形成自环）；否则会产生 \(w_1+w_2\) 的代价。如果 \(w_1<w_2\) 则可以直接对 \(w_1\) 进行后续操作，一定更优；否则不会移动 \(w_1\)，也不会更劣。

具体可以有如下策略：

不走自己。此时对于边权为 \(w\) 的边 \((u,v)\)，可以通过 \(w\min(dis(1,u)+dis(v,n),dis(1,v)+dis(u,n))\) 的代价使其直接连接 \(1,n\)。
走自己。此时对于边权为 \(w\) 的边 \((u,v)\)，枚举其形成的自环 \((p,p)\)，则可以通过 \(w(dis(1,p)+dis(p,n)+\min(dis(u,p),dis(v,p))+1)\) 的代价使其直接连接 \(1,n\)。形成自环后不会使得图其他部分的连通性改变，所以最多只会形成一次自环。

上面的 \(dis(u,v)\) 为原图中 \(u\) 到 \(v\) 的路径上的最少边数。

代码

CF1737E Ela Goes Hiking

可以将所有蚂蚁分为若干连续段，满足每个连续段内有且只有最后一只蚂蚁向左，其余蚂蚁都向右。（此时第 \(n\) 只蚂蚁无论方向如何，因为挡板其最后一定会向左；同理第一只蚂蚁一定会向右）此时某只蚂蚁要存活当且仅当其作为这只最右端的蚂蚁。

淘汰掉最开始向右的蚂蚁之后，某只蚂蚁此时的重量为其所在连续段内蚂蚁之和。设此时第 \(i\) 只蚂蚁重量为 \(w_i\)，则 \(i\) 所在连续段左端，能够存活的唯一蚂蚁重量一定为 \(i-w_i\)，此时第 \(i\) 只蚂蚁存活需要 \(w_i\ge i-w_i\)，也就是 \(w_i\ge \lfloor\frac i2\rfloor\)。此时 \(i\) 之前的最后 \(\lfloor\frac i2\rfloor\) 只蚂蚁一定需要向右，其他蚂蚁方向无所谓，可得其在 \(1\sim i\) 内存活的方案数为 \(2^{\lfloor\frac i2\rfloor}\)。（也可以理解为 \(1+\sum_{j=0}^{\lfloor\frac i2\rfloor-1}2^j\)，\(1\) 表示最左端蚂蚁有两种方向）

然后第 \(i\) 只蚂蚁在 \(1\sim i\) 内存活时重量为 \(i\)。考虑 dp 计算其在 \(i\sim n\) 内存活的方案数，设 \(dp_j\) 为重量为 \(j\) 的蚂蚁能吃掉后面 \(n-j\) 只蚂蚁的方案数，枚举第 \(i\) 只蚂蚁吃掉的下一只蚂蚁的重量，则转移有 \(dp_i=\sum_{j=i+1}^{2i-1} dp_j\)。初值有 \(dp_n=1\)。这部分可以用后缀和优化，可得总复杂度为 \(O(n)\)。

代码

CF1746B Rebellion

考虑最后的不降序列一定可以被分为 \(0\) 和非 \(0\) 的两段。对于全 \(0\) 段，其中原有的 \(1\) 一定需要加到非 \(0\) 段内（先加到非 \(0\) 段的 \(0\) 上，再加到某个后缀内）；对于非 \(0\) 段，其中原有的 \(0\) 一定需要删除或变为 \(1\)。对这两个数量取 \(\max\) 即可。

代码

CF1746C Permutation Oddness

考虑差分。对 \(a\) 的某个后缀加 \(v\) 相当于对 \(a\) 的差分序列对应的某个位置加 \(v\)。

显然对于每个 \(i\)，差分序列中的不大于 \(-i\) 的数不会出现超过 \(n-i\) 次，所以可以直接把每个成为负数的差分升序排序，然后降序安排上 \(n\sim 1\) 操作即可。

代码

CF1746D Paths on the Tree

设 \(dp_{u,i}\) 为在节点 \(u\) 上安排了 \(i\) 条路径的最大价值。设 \(j=\frac i{|son_u|}\)，转移有：

\[dp_{u,i}=\sum_{v\in son_u}dp_{v,\lfloor j\rfloor}+\sum_{v\in son_u}(dp_{v,\lceil j\rceil}-dp_{v,\lfloor j\rfloor})[是前\ i\bmod |son_u|\ 大者] \]

计算 \(dp_{u,i}\) 时，对于 \(i\) 节点的某个子节点 \(v\)，只会计算 \(dp_{v,\lceil j\rceil}\) 和 \(dp_{v,\lfloor j\rfloor}\)。然后对于 \(v\) 的子节点，最多会代入 \(\lfloor\frac {j}{|son_v|}\rfloor,\lfloor\frac {j+1}{|son_v|}\rfloor,\lceil\frac j{|son_v|}\rceil,\lceil\frac {j+1}{|son_v|}\rceil\) 进行计算。可以发现这四个数的值最多只会出现两个相邻的值，故使用记忆化搜索的时空复杂度均为 \(O(n)\) 的。

代码

CF1746E1 Joking

考虑如何在有限次操作内将某个范围尽量缩小。显然不能通过二分的方式找答案，考虑将范围分为更多份再查询。下面给出两种操作：

考虑将范围分为四份 \(S_1,S_2,S_3,S_4\)，然后询问 \(S_1,S_2\) 和 \(S_1,S_3\)。如果均答为存在则排除 \(S_4\)；均答为不存在则排除 \(S_1\)；答只存在于前者则排除 \(S_3\)；只存在于后者则排除 \(S_2\)。这样则在两次询问内将答案范围缩小了 \(\frac 14\)。询问范围内只有三个数时可以按下面一种方式确定。
考虑将范围分为三份 \(S_1,S_2,S_3\)，然后询问 \(S_1\)，\(S_1\)。如果均答不存在则可以排除 \(S_1\)；如果某次答存在则问 \(S_2\)；此时问 \(S_1/S_2\) 中一定有一次是真的，如果问 \(S_2\) 答不存在则排除 \(S_2\)，否则排除 \(S_3\)。这样则在三次询问内将答案范围缩小了 \(\frac 13\)。

问题的关键在于枚举回答为真真/假真/真假的情况，然后让这三者的答案共同确定这个数不在的集合。

代码（第二种做法）

CF1746F Kazaee

考虑随机化算法。

可以把每个值赋一个随机数，询问的时候就等效于判断区间和是否为 \(k\) 的倍数。然后单次进行询问时的出错概率在 \(k=2\) 时最大，为 \(\frac 12\)；在 \(k>2\) 时也有一定的出错概率。此时可以进行 \(O(\log)\) 次判断，将出错概率进一步降低。

也可以对原数组建 \(O(\log)\) 个随机子集，询问时判断每个子集内的所有数出现次数之和是否为 \(k\) 的倍数即可。原理和上面的类似。

代码

注意为了减少空间占用，第一种做法需要将一个数的 \(O(\log)\) 个哈希值压缩成一个结构体再建 map。而且这个题中使用 unordered_map 代替 map 后时间和空间都更加优秀。

Make Nonzero Sum CF1753A1,CF1753A2

由于每个区间的价值减去区间和一定为偶数，显然 \(1/-1\) 的数量之和为奇数则无解。考场上一直在想某些位置被分至连续段的第偶数处的贡献，然后寄了。（~~可以说 A1/A2 的思维难度甚至 > B~~）

对于 A1，可以把相邻每两个数进行考虑。如果相邻两数相同，则将它们分为一个连续段内，否则将它们分至两个连续段。然后对于 A2 里出现了 \(0\) 的情况，仍然可以把相邻一对 \(1/-1\) 一起进行考虑。设某对相邻的非 \(0\) 数的位置分别为 \(x,y\)，则两数不同时需要确保它们在连续段内奇偶性不同的位置，将 \([x,y]\) 分为 \([x,y-1]\) 和 \([y,y]\)；否则需要确保它们在连续段内奇偶性相同的位置，如果 \(y-x=1\) 则将 \([x,y]\) 分为 \([x,y]\)，否则分为 \([x,y-2]\) 和 \([y-1,y]\)。

代码

CF1753D The Beach

代码

ARC151C 01 Game

这个人在 2022 年 11 月 9 号学会了 SG 函数 / SG 定理。（下面抄书）

引入：Nim 博弈

定义

有 \(n\) 堆物品，第 \(i\) 堆物品有 \(a_i\) 个，先手和后手轮流操作，每次在某一堆中取若干个物品，但是不能不取。问先后手均采取最优策略的情况下谁会胜。

定理

在 Nim 博弈中，先手必胜当且仅当 \(\bigoplus_{i=1}^n a_i\ne 0\)。

证明

考虑 \(X=\bigoplus_{i=1}^n a_i\ne 0\) 的情况。设 \(X\) 的最高位为 \(1\)，则此时一定存在某个 \(a_i\) 满足 \(a_i\) 的这一位同样是 \(1\)。由于 \(a_i\oplus X\) 的这一位为 \(0\)，最高位小于 \(a_i\) 的最高位，有 \(a_i\ge a_i\oplus X\)，所以先手可以将 \(a_i\) 变为 \(a_i\oplus X\)，此时新的 \(\bigoplus_{i=1}^n a_i=0\)。然后在 \(\bigoplus_{i=1}^n a_i=0\) 时，当前操作者一定不能进行操作使得 \(\bigoplus_{i=1}^n a_i=0\)，其对手仍然可以将操作后的的 \(\bigoplus_{i=1}^n a_i\) 变为 \(0\)，直到 \(a_1=a_2=\cdots=a_n=0\)。

引入2：公平组合游戏

如果某个游戏满足：

由两名玩家交替行动；
在游戏进程的任意时刻，可以执行的合法行动与轮到哪名玩家无关（e.g. 象棋/围棋即不是公平组合游戏）；
无法行动者判负。

则称该游戏为一个公平组合游戏。

有向图游戏

给定一个 DAG，图中有唯一的一个起点 \(s\)，在起点上有一枚棋子，先后手交替地将棋子进行移动，每次只能移动一步，无法操作者判负。此时该游戏被称为有向图游戏。

显然每一个公平游戏均等效于一个有向图游戏。

SG 函数

在有向图游戏中，对于每个节点 \(x\)，定义其 SG 函数值为其所有后继节点的 SG 函数构成的集合的 \(\rm{mex}\)。特别地，定义无出度的 SG 值为 \(0\)，整个有向图的 SG 值为起点的 SG 值。

此时无出度的点显然后手必胜。对于某个点，如果其 SG 值非 \(0\)，则先手可以把这个点上的棋子移到 SG 值为 \(0\) 的点。如果某个点的 SG 值为 \(0\)，则先手无论怎样将这个点上的棋子移动，后手均能够将移动后的棋子移动到 SG 值仍然为 \(0\) 的点上，直到移动到出度为 \(0\) 的点。所以某个有向图先手必胜的充要条件为起点的 SG 值非 \(0\)。

SG 定理

有 \(n\) 个有向图游戏 \(G_1\sim G_n\)。定义某个游戏 \(G\) 的规则为：每名玩家选择某个 \(G_i\)，将其上面的棋子移动一步，无法操作者判负。（显然 \(G\) 也是一个有向图游戏）

此时定义 \(G\) 的 SG 值为 \(\bigoplus_{i=1}^n SG(G_i)\)。此时 \(G\) 满足先手必胜的充要条件是 \(\bigoplus_{i=1}^n SG(G_i)\ne 0\)。

SG 定理证明

如果只考虑从某个点走到 SG 值更小的点，则每一步等效于将某个 \(G_i\) 的 SG 值减小为任意正整数（但不能不减小），证明考虑 Nim 博弈的证明。

考虑从某个点到 SG 值更大的点的操作。按照上述的操作，胜者一定可以在每一步将棋子移动到 SG 值更小的点上。此时对手如果把棋子从某个点移动到 SG 值更大的点上，胜者一定可以将棋子移动到 SG 值相同的点上。根据 DAG 的性质，对手一定在若干步后无法执行这样的操作。

特别地，Nim 博弈中转为无向图后，每个 \(a_i\) 等效于一个 SG 值为 \(a_i\) 的有向图游戏，且不能从某个点移到 SG 值更大的点上。

考虑 SG 定理。原局面显然可以分为若干个互不干扰的局面（可视为若干个有向图游戏），且每一步可以把某个有向图游戏分为多个游戏。

对于两端不同的某一格，显然 SG 值为 \(0\)；对于两端相同的一格，其 SG 值为 \(1\)。显然某个连续段对应先手是否必胜只和连续段长度和两端是否相同有关。设 \(\{d,0/1/2/3\}\) 分别表示两端没有数/一段没有数/两端相同/两端不同的长为 \(d\) 的连续段，则 SG 函数计算方式如下（一定要注意将要填的数和边界相连的情况，最好特判，否则会产生非常奇怪的错误结论）：

初值有 \(SG(\{1,0\})=SG(\{1,1\})=SG(\{1,2\})=1,SG(\{1,3\})=0\)。

\(\forall d\ge 2,\)

\[\begin{aligned}SG(\{d,0\})&={\rm{mex}}_{i=0}^{d-1}\{SG(\{i,1\})\oplus SG(\{d-i-1,1\})\}\\SG(\{d,1\})&={\rm{mex}}\{SG(\{d-1,1\}),SG(\{d-1,2\}),SG(\{d-1,3\}),{\rm{mex}}_{i=1}^{d-2}\{SG(\{i,1\})\oplus SG(\{d-i-1,2\}),SG(\{i,1\})\oplus SG(\{d-i-1,3\})\}\}\\SG(\{d,2\})&={\rm{mex}}(SG(\{d-1,3\}),{\rm{mex}}_{i=1}^{d-2}\{SG(\{i,2\})\oplus SG(\{d-i-1,2\}),SG(\{i,3\})\oplus SG(\{d-i-1,3\})\}\\SG(\{d,3\})&={\rm{mex}}(SG(\{d-1,2\}),{\rm{mex}}_{i=1}^{d-2}\{SG(\{i,2\})\oplus SG(\{d-i-1,3\})\})\end{aligned} \]

可以通过打表等方式证明：\(\forall d>0, SG(\{d,0\})=d\bmod 2,SG(\{d,1\})=d,SG(\{d,2\})=1,SG(\{d,3\})=0\)。

代码

ARC151D Binary Representations and Queries

考虑在先后执行 \(X=j,X=k(j\ne k)\) 的操作后，对于某个数 \(a\) 会造成怎样的影响。

发现每个数在 \(X=j\) 时与其构成转移的数是确定的，且每个数只会从不超过 \(1\) 个数转移而来，则对于某个 \(a\)，如果其在两次操作中均能转移到其他数，则转移方式如下：

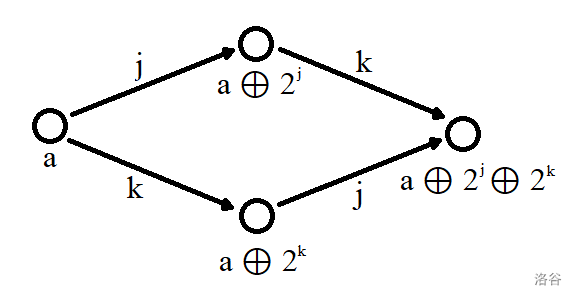
此时对于 \(a\oplus 2^j\oplus 2^k\)，其在最后的值和两次操作的顺序无关。且如果存在 \(a\rightarrow a\oplus 2^j\rightarrow a\oplus 2^j\oplus 2^k\) 的转移，由于 \(a\) 和 \(a\oplus 2^j\) 的第 \(k\) 位相同，则一定存在 \(a\rightarrow a\oplus 2^k\rightarrow a\oplus 2^j\oplus 2^k\) 的转移。

在确定 \(X\) 值不同的操作可以交换顺序后，可以把 \(X\) 值相同的所有操作一起处理，维护系数，以在 \(O(n2^n)\) 的时间内完成所有操作。

代码

ABC269G Reversible Cards 2

考虑每张卡片翻过来后，对朝上的数字和造成的贡献为 \(b_i-a_i\)。将 \(b_i-a_i\) 相同者合并之后，问题即转化为一个多重背包问题。同时 \(\sum_{i=1}^n (a_i+b_i)=m\) 意味着 \(\sum_{i=1}^n (\max(a_i,b_i)-\min(a_i,b_i))\le m\)。此时显然 \(\max(a_i,b_i)-\min(a_i,b_i)\) 的取值只会有 \(O(\sqrt m)\) 种，也就意味着 \(b_i-a_i\) 也只有 \(O(\sqrt m)\) 种。单调队列优化多重背包即可。（为什么这么【】的题我一直没想出来