CSP-S 2022 题解

属于是考后就会考时就废了属于是。

P8817 假期计划 Holiday

题意

有一张 \(n\) 个点 \(m\) 条边的无向图，第 \(i\) 个点有点权 \(v_i\)。需要在图上找出 \(4\) 个不同的点 \(a,b,c,d\)，满足 \(1\rightarrow a,a\rightarrow b,b\rightarrow c,c\rightarrow d,d\rightarrow 1\) 的最短路均不超过 \(k+1\)，求合法的 \(a,b,c,d\) 的 \(\max(v_a+v_b+v_c+v_d)\) 值。\(n\le 2.5\times 10^3,m\le 10^4,k\le 10^2\)。

解法

对于某个点 \(u\)，考虑其作为 \(b/c\) 的贡献，然后合并两个点对应的答案。此时可以对于每个 \(u\)，维护满足 \(x\rightarrow u\) 的最短路不超过 \(k+1\)，且 \(v_x\) 前三大的点 \(x\)。可以发现将满足 \(x\rightarrow y\) 最短路不超过 \(k+1\) 的 \(x,y\) 维护的内容整合后，一定可以得出一组满足要求的解。

代码

点此查看代码

#include <bits/stdc++.h>
using namespace std;
const int maxn=2510;
const int maxm=20010;
int n,i,j,k,p,u,v,t,l,r;
int h[maxn],q[maxn],*f;
int g[maxn][maxn],m[maxn][3];
long long ans,va[maxn];
struct edge{int to,nxt;}E[maxm];
int main(){
    freopen("holiday.in","r",stdin);
    freopen("holiday.out","w",stdout);
    scanf("%d%d%d",&n,&p,&k); k+=2;
    for(i=2;i<=n;++i) scanf("%lld",va+i);
    while(p--){
        scanf("%d%d",&u,&v);
        E[++t]={u,h[v]}; h[v]=t;
        E[++t]={v,h[u]}; h[u]=t;
    }
    for(i=1;i<=n;++i){
        f=g[i]; f[i]=1;
        l=r=1; q[1]=i;
        while(l<=r){
            u=q[l++];
            if(f[u]==k) continue;
            t=f[u]+1;
            for(j=h[u];j;j=E[j].nxt){
                v=E[j].to;
                if(f[v]) continue;
                f[v]=t; q[++r]=v;
            }
        }
        f[i]=0;
    }
    for(i=2;i<=n;++i){
        if(!g[1][i]) continue;
        for(j=2;j<=n;++j){
            if(!g[i][j]) continue;
            for(k=0;k<3;++k){
                if(va[m[j][k]]<va[i]){
                    for(p=2;p>k;--p) m[j][p]=m[j][p-1];
                    m[j][k]=i; break;
                }
            }
        }
    }
    for(i=2;i<=n;++i){
        for(k=0;k<3&&m[i][k];++k){
            u=m[i][k];
            for(j=2;j<=n;++j){
                if(j==u||!g[i][j]) continue;
                for(p=0;p<3&&m[j][p];++p){
                    v=m[j][p]; if(v==i||v==u) continue;
                    ans=max(ans,va[i]+va[u]+va[j]+va[m[j][p]]);
                }
            }
        }
    }
    printf("%lld",ans);
    return 0;
}

P8818 策略游戏 Game

题意

有一个长为 \(n\) 的数组 \(a\) 和一个长为 \(m\) 的数组 \(b\)。现在有 \(q\) 次操作，第 \(i\) 次操作中先手会选取 \(a\) 中 \([l_1,r_1]\) 内的一个数 \(a_x\)，后手会 根据 \(\boldsymbol{a_x}\) 选取 \(b\) 中 \([l_2,r_2]\) 内的一个数 \(b_y\)；先手会最大化 \(a_xb_y\)，而后手会最小化 \(a_xb_y\)，两者均会选择最优方法。求每次操作的 \(a_xb_y\) 值。\(n,m,q\le 10^5\)。

解法

如果 \(a_x>0\)，则后手一定会选择区间内最小值；而如果最小值大于 \(0\)，则先手会选择最大的正数，否则会选择最小的正数。

如果 \(a_x<0\)，则后手一定会选择区间内最大值；而如果最大值小于 \(0\)，则先手会选择最小的负数，否则会选择最大的负数。

如果 \(a_x=0\)，则先手可以使答案不小于 \(0\)。

综合上述三种情况讨论即可。

代码

点此查看代码

#include <bits/stdc++.h>
using namespace std;
const int maxl=20;
const int maxn=100010;
int n,m,q,i,j,d,a,t,lx,ly,rx,ry;
int v[maxn],lb[maxn];
int s[4][maxl][maxn],b[2][maxl][maxn];
long long nw,cx,ans;
int QueA(int id,int l,int r){
    int le=lb[r-l+1];
    if(id&1) return max(s[id][le][l],s[id][le][r-(1<<le)+1]);
    return min(s[id][le][l],s[id][le][r-(1<<le)+1]);
}
int QueB(bool id,int l,int r){
    int le=lb[r-l+1];
    if(id) return max(b[id][le][l],b[id][le][r-(1<<le)+1]);
    return min(b[id][le][l],b[id][le][r-(1<<le)+1]);
}
bool QueZ(int l,int r){return (*lower_bound(v+1,v+t+1,l))<=r;}
int main(){
    freopen("game.in","r",stdin);
    freopen("game.out","w",stdout);
    memset(s[0],0x3f,sizeof(s[0]));
    memset(s[3],0xc0,sizeof(s[3]));
    for(i=2;i<maxn;++i) lb[i]=lb[i>>1]+1;
    scanf("%d%d%d",&n,&m,&q);
    for(i=1;i<=n;++i){
        scanf("%d",&a);
        if(a>0) s[0][0][i]=s[1][0][i]=a;
        else if(a<0) s[2][0][i]=s[3][0][i]=a;
        else v[++t]=i;
    }
    v[t+1]=n+1;
    for(i=1;i<=m;++i){
        scanf("%d",b[0][0]+i);
        b[1][0][i]=b[0][0][i];
    }
    for(j=1;j<maxl;++j){
        d=m-(1<<j)+1;
        for(i=1;i<=d;++i){
            b[0][j][i]=min(b[0][j-1][i],b[0][j-1][i+(1<<(j-1))]);
            b[1][j][i]=max(b[1][j-1][i],b[1][j-1][i+(1<<(j-1))]); 
        }
        d=n-(1<<j)+1;
        for(i=1;i<=d;++i){
            s[0][j][i]=min(s[0][j-1][i],s[0][j-1][i+(1<<(j-1))]);
            s[1][j][i]=max(s[1][j-1][i],s[1][j-1][i+(1<<(j-1))]); 
            s[2][j][i]=min(s[2][j-1][i],s[2][j-1][i+(1<<(j-1))]);
            s[3][j][i]=max(s[3][j-1][i],s[3][j-1][i+(1<<(j-1))]); 
        }
    }
    for(i=1;i<=q;++i){
        scanf("%d%d%d%d",&lx,&ly,&rx,&ry);
        if(QueZ(lx,ly)) ans=0; else ans=-LLONG_MAX;
        cx=QueB(0,rx,ry); nw=QueA(cx>=0,lx,ly); 
        if(nw!=0x3f3f3f3f&&nw>0) ans=max(ans,nw*cx);
        cx=QueB(1,rx,ry); nw=QueA(2+(cx>0),lx,ly);
        if(nw!=(signed)0xc0c0c0c0&&nw<0) ans=max(ans,nw*cx);//这里 0xc0c0c0c0 需要强转成 signed int！！！！
        printf("%lld\n",ans);
    }
    return 0;
}

P8819 星战 Galaxy

题意

有一张 \(n\) 个点 \(m\) 条边的有向图，初始时所有边均可通行。有以下四种操作：

• 使某条边不可通行（保证其之前可通行）；
• 使某个点的所有入边不可通行；
• 使某条边可通行（保证其之前不可通行）；
• 使某个点的所有入边可通行。

每次操作后，询问每个点是否有且只有一条可通行的出边。\(n,m,q\le 5\times 10^5\)。

解法

注意我们只需要维护每个点是否只有一条可通行的出边。考虑哈希，设第 \(i\) 个点的每条可通行的出边的哈希值为 \(H_i\)，则可以维护可通行的出边总数是否为 \(n\) 且出边的哈希值的异或和是否为 \(\bigoplus_{i=1}^n H_i\)。美其名曰 Xor Hashing（当然维护 \(H\) 值之和也是可行的，美其名曰 Sum Hashing）

可以对于每个点维护其可通行的所有入边的数量和哈希值，方便维护第二/第四种操作。

代码

点此查看代码

#include <bits/stdc++.h>
using namespace std;
const int maxn=500010;
mt19937_64 Rand(time(0));
int n,m,i,u,v,q,k,c[maxn],s[maxn];
unsigned long long w,sm,ac,h[maxn],ha[maxn],hn[maxn];
int main(){
    freopen("galaxy.in","r",stdin);
    freopen("galaxy.out","w",stdout);
    scanf("%d%d",&n,&m);
    for(i=1;i<=n;++i) ac^=(h[i]=Rand());
    for(i=1;i<=m;++i){
        scanf("%d%d",&u,&v);
        ++c[v]; ha[v]^=h[u]; 
    }
    for(i=1;i<=n;++i){
        s[i]=c[i];
        sm^=(hn[i]=ha[i]);
    }
    scanf("%d",&q);
    while(q--){
        scanf("%d%d",&k,&u);
        if(k&1){
            scanf("%d",&v); w=h[u];
            sm^=w; ha[v]^=w;
            if(k==1) --c[v],--m; 
            else ++c[v],++m;
        } 
        else{
            if(k==2){
                m-=c[u]; sm^=ha[u];
                ha[u]=c[u]=0;
            }
            else{
                m+=s[u]-c[u]; sm^=hn[u]^ha[u];
                ha[u]=hn[u]; c[u]=s[u];
            }
        }
        if(m==n&&sm==ac) printf("YES\n");
        else printf("NO\n");
    }
    return 0;
}

P8820 数据传输 Transmit

题意

有一棵大小为 \(n\) 的树，同时有一张 \(n\) 个点的无向图，对于一对点 \(u,v\)，如果它们在树上的距离不超过 \(k\)，则图上存在边 \(u\leftrightarrow v\)。第 \(i\) 个点有点权 \(V_i\)。\(q\) 组询问，每次询问图中 \(u\) 到 \(v\) 的所有路径中，经过的点的最小点权和。\(n,q\le 2\times 10^5,k\le 3\)。

解法

下面先讨论 \(q=1\) 的情况。

\(k=1\) 可以直接计算链上 \(V\) 值和，\(k=2\) 可以只用把路径上的 \(V\) 值拿出来 dp。

而在 \(k=3\) 的时候，可能会取路径外的点的 \(V\) 值作为最终答案（也就是样例 2 的某个数据）。但是取不与路径上某个节点直接相连的点一定不是最优的（可以被跳过），（设答案取到了与 \(u\) 相邻的点 \(v\) 的 \(V\) 值）如果 \(v\) 不是与 \(u\) 相邻的点中 \(V\) 值最小者，则 \(v\) 取相邻的点的 \(V\) 值最小者（可能就在路径上，此时这个决策一定不会最优）一定更优。

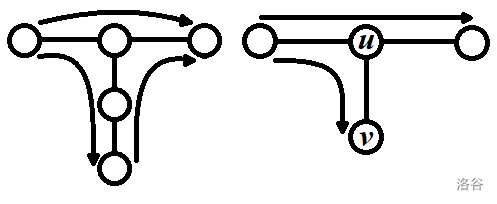
可以维护与 \(u\) 相邻的点的最小 \(V\) 值 \(m_u\)。此时设 \(dp_{u,0}\) 和 \(dp_{u,1}\) 为考虑到 \(u\)，是否取到路径之外与 \(u\) 相邻的节点时，取的 \(V\) 值之和的最小值，转移时需要维护其之前三个点的 dp 值 \(dp_{v_1,0/1},dp_{v_2,0/1},dp_{v_3,0}\)，则 \(dp_{u,0}=\min(dp_{v_1,0/1},dp_{v_2,0/1},dp_{v_3,0})+V_u,dp_{u,1}=\min(dp_{v_1,1},dp_{v_2,0})+m_u\)。设起点为 \(x\)，终点为 \(y\)；则初值为 \(dp_{x,0}=V_x,dp_{x,1}=+\infty\)，目标为 \(dp_{y,0}\)。

然后考虑 \(q>1\) 的情况。考虑使用矩阵乘法维护对应 dp 转移。不难写出下面的转移方式：

\(k=3\) 时有下述转移：

\[\begin{bmatrix}V_u&V_u&V_u&V_u&V_u\\+\infty&m_u&m_u&+\infty&+\infty\\0&+\infty&+\infty&+\infty&+\infty\\+\infty&0&+\infty&+\infty&+\infty\\+\infty&+\infty&0&+\infty&+\infty\end{bmatrix}\times\begin{bmatrix}dp_{v_1,0}\\dp_{v_1,1}\\dp_{v_2,0}\\dp_{v_2,1}\\dp_{v_3,0}\end{bmatrix}=\begin{bmatrix}dp_{u,0}\\dp_{u,1}\\dp_{v_1,0}\\dp_{v_1,1}\\dp_{v_2,0}\end{bmatrix} \]

\(k=2\) 时可以有下述转移：

\[\begin{bmatrix}V_u&+\infty&V_u&+\infty&+\infty\\+\infty&+\infty&+\infty&+\infty&+\infty\\0&+\infty&+\infty&+\infty&+\infty\\+\infty&0&+\infty&+\infty&+\infty\\+\infty&+\infty&0&+\infty&+\infty\end{bmatrix}\times\begin{bmatrix}dp_{v_1,0}\\dp_{v_1,1}\\dp_{v_2,0}\\dp_{v_2,1}\\dp_{v_3,0}\end{bmatrix}=\begin{bmatrix}dp_{u,0}\\dp_{u,1}\\dp_{v_1,0}\\dp_{v_1,1}\\dp_{v_2,0}\end{bmatrix} \]

\(k=1\) 时可以有下述转移：

\[\begin{bmatrix}V_u&+\infty&+\infty&+\infty&+\infty\\+\infty&+\infty&+\infty&+\infty&+\infty\\0&+\infty&+\infty&+\infty&+\infty\\+\infty&0&+\infty&+\infty&+\infty\\+\infty&+\infty&0&+\infty&+\infty\end{bmatrix}\times\begin{bmatrix}dp_{v_1,0}\\dp_{v_1,1}\\dp_{v_2,0}\\dp_{v_2,1}\\dp_{v_3,0}\end{bmatrix}=\begin{bmatrix}dp_{u,0}\\dp_{u,1}\\dp_{v_1,0}\\dp_{v_1,1}\\dp_{v_2,0}\end{bmatrix} \]

上述乘法为广义矩阵乘法，有 \((A\times B)_{i,j}=\min_k\{A_{i,k}+B_{k,j}\}\)。这样处理则转移时直接倍增出路径的两部分对应的矩阵积即可。

但是空间会超 1024 MB 然后寄掉。令 \(f_u=dp_{u,0},f_{v_1}=\min(dp_{u,1},dp_{v_1,0}),f_{v_2}=\min(dp_{v_1,1},dp_{v_2,0})\)（考虑合并 \(dp_{v_1,0},dp_{u,1}\) 和 \(dp_{v_2,0},dp_{v_1,1}\)），则可以重新设计转移如下：

\(k=3\) 时有如下转移：

\[\begin{bmatrix}V_u&V_u&V_u\\0&m_u&+\infty\\+\infty&0&+\infty\end{bmatrix}\times\begin{bmatrix}f_{v_1}\\f_{v_2}\\f_{v_3}\end{bmatrix}=\begin{bmatrix}f_u\\f_{v_1}\\f_{v_2}\end{bmatrix} \]

\(k=2\) 时可以有如下转移：

\[\begin{bmatrix}V_u&V_u&+\infty\\0&+\infty&+\infty\\+\infty&0&+\infty\end{bmatrix}\times\begin{bmatrix}f_{v_1}\\f_{v_2}\\f_{v_3}\end{bmatrix}=\begin{bmatrix}f_u\\f_{v_1}\\f_{v_2}\end{bmatrix} \]

\(k=1\) 时可以有如下转移：

\[\begin{bmatrix}V_u&+\infty&+\infty\\0&+\infty&+\infty\\+\infty&0&+\infty\end{bmatrix}\times\begin{bmatrix}f_{v_1}\\f_{v_2}\\f_{v_3}\end{bmatrix}=\begin{bmatrix}f_u\\f_{v_1}\\f_{v_2}\end{bmatrix} \]

代码

点此查看代码

#include <bits/stdc++.h>
using namespace std;
#define ll long long
const int maxl=18;
const int maxn=200010;
int n,q,i,j,k,u,v,t,pi,pj;
int h[maxn],va[maxn],dep[maxn],fa[maxl][maxn];
ll w;
struct edge{int to,nxt;}E[maxn<<1];
struct mat{
    ll a[3][3];
    mat operator *(const mat &x)const{
        mat tmp;
        for(pi=0;pi<3;++pi)
            for(pj=0;pj<3;++pj)
                tmp.a[pi][pj]=min(min(a[pi][0]+x.a[0][pj],
                                      a[pi][1]+x.a[1][pj]),
                                  min(a[pi][2]+x.a[2][pj],
                                        0x3f3f3f3f3f3f3f3fLL));
        return tmp;
    } 
}um[maxl][maxn],dm[maxl][maxn],I,xm,ym;
void dfs(int p,int f){
    dep[p]=dep[f]+1;
    int lp,to;
    for(lp=h[p];lp;lp=E[lp].nxt){
        to=E[lp].to;
        if(to==f) continue;
        fa[0][to]=p; dfs(to,p);
    }
}
int lca(int x,int y){
    for(j=maxl-1;j>=0;--j) if(dep[fa[j][x]]>=dep[y]) x=fa[j][x];
    if(x==y) return x;
    for(j=maxl-1;j>=0;--j) if(fa[j][x]!=fa[j][y]) x=fa[j][x],y=fa[j][y];
    return fa[0][x];
}
int main(){
    freopen("transmit.in","r",stdin);
    freopen("transmit.out","w",stdout);
    memset(&I,0x3f,sizeof(I));
    memset(&xm,0x3f,sizeof(xm));
    xm.a[1][0]=xm.a[2][1]=
     I.a[0][0]=I.a[1][1]=I.a[2][2]=0;
    scanf("%d%d%d",&n,&q,&k);
    for(i=1;i<=n;++i) scanf("%d",va+i);
    for(i=1;i<n;++i){
        scanf("%d%d",&u,&v);
        E[++t]={u,h[v]}; h[v]=t;
        E[++t]={v,h[u]}; h[u]=t;
    }
    for(i=1;i<=n;++i){
        xm.a[0][0]=w=va[i];
        if(k!=1){
            xm.a[0][1]=w;
            if(k!=2){
                xm.a[0][2]=w; w=xm.a[2][2]; 
                for(j=h[i];j;j=E[j].nxt) w=min(w,(ll)va[E[j].to]);
                xm.a[1][1]=w;
            }
        }
        um[0][i]=dm[0][i]=xm;
    }
    dfs(1,0);
    for(j=1;j<maxl;++j){
        for(i=1;i<=n;++i){
            fa[j][i]=fa[j-1][fa[j-1][i]];
            um[j][i]=um[j-1][i]*um[j-1][fa[j-1][i]];
            dm[j][i]=dm[j-1][fa[j-1][i]]*dm[j-1][i];
        }
    }
    while(q--){
        scanf("%d%d",&u,&v); 
        if(dep[u]<dep[v]) swap(u,v);
        t=lca(u,v); i=va[u]; 
        u=fa[0][u]; xm=ym=I; 
        for(j=maxl-1;j>=0;--j){
            if(dep[fa[j][u]]>=dep[t]){
                xm=dm[j][u]*xm;
                u=fa[j][u];
            }
            if(dep[fa[j][v]]>=dep[t]){
                ym=ym*um[j][v];
                v=fa[j][v];
            }
        }
        printf("%lld\n",((ym*um[0][t])*xm).a[0][0]+i);
    }
    return 0;
}