初步学习线段树
假如给你一组数，要求你做若干个操作，操作有两种： 1、把一个区间的数加上k。 2、查询某个区间的区间和
显然我们可以用O（N）的时间复杂度完成这两个操作。
但假如操作个数和N的规模非常大，比如达到了10^5的规模，那么朴素做法就太慢了。因此，我们需要一个新的东西——线段树。
什么是线段树（Segment Tree）？
线段树是一种二叉搜索树，与区间树相似，它将一个区间划分成一些单元区间，每个单元区间对应线段树中的一个叶结点。 对于线段树中的每一个非叶子节点[a,b]，它的左儿子表示的区间为[a,(a+b)/2]，右儿子表示的区间为[(a+b)/2+1,b]。因此线段树是平衡二叉树，最后的子节点数目为N，即整个线段区间的长度。(摘自百度百科)。
简单的说就是在树上的每一个节点存储一个区间上的信息，一个点的左右儿子分别储存该点所存的左半个区间和右半个区间。
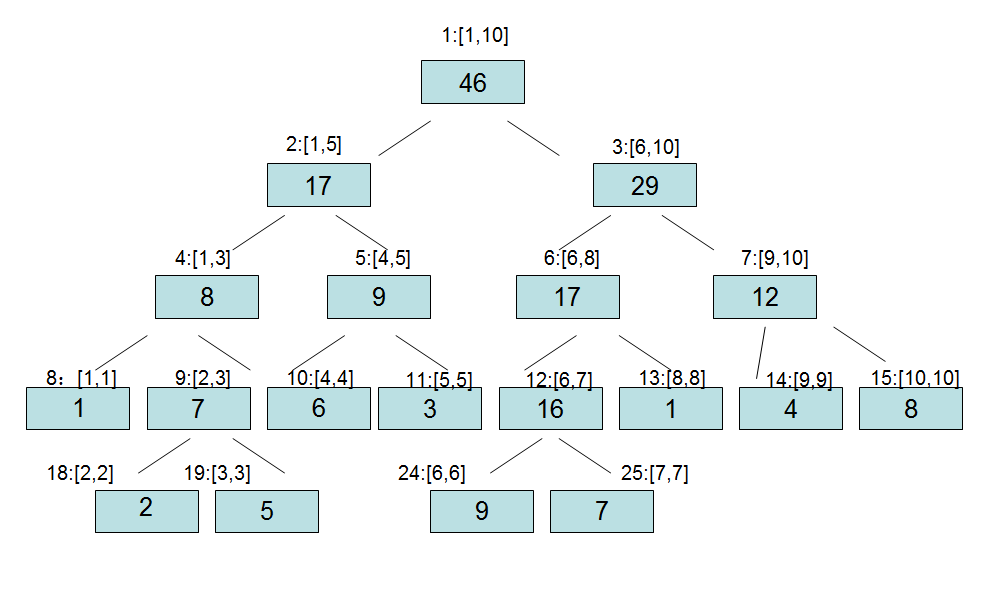
举个栗子，假如给我们一组数1,2,6,3,8,9,5,7,4,5，我们想储存每个区间的区间和。那么这个线段树大概长这样：
（每个节点存储节点所代表区间的区间和）
线段树可以做什么？
线段数支持：
单点/区间修改（update）
单点/区间查询 （query）
它们的时间复杂度都是O（log n）的
做法（思路）
建树（build）：我们要每次二分一个区间，然后分别存入左右儿子中，这个过程是相似的，因此我们可以用递归完成建树。当区间长度为1时，我们把数列中数的值存入叶子结点，然后向上传递。
更新（update）：如果我们要更新某一段区间A的值，那么显然我们只需要递归更新区间中每一个数的值，然后回溯时更新父节点的值。
我们依然递归完成这个任务，但update和build有一些区别，我们来思考。（下面的假设请对照上图）
假如我们要修改\([2,2]\) , 那么我们直接简单的递归到\([2,2]\)然后向上更新父节点的值即可。
假如我们要更新\([4,6]\)，那么问题来了，这个区间处在两个子树中，我们无法找到直接代表这个区间的节点。但这样我们就没办法修改了吗？不是的。我们可以把\([4,6]\)拆成\([4,5]\)和\([6,6]\)分别修改。这只需要在向下递归时加一个判断。
查询（query）：查询的步骤和更新是相似的。
优化
实际上，这样的线段树还不是足够快的，每次我们更新了所要修改的区间A所在的节点，A所包含的区间，和包含A的区间，有没有办法优化这件事情使它更新的节点少一些呢？？
答案是有的，我们可以先不更新A所包含的区间。然后引入一个懒标记，记录当前节点未向下传递的修改。
也就是说假如我想给\([4,5]\)每个数加上\(k\)，然后我们就只需要给\([4,5]\)这个节点加上\((5-4)k\),\((区间长度*k)\)，然后在\([4,5]\)的懒标记上记录下\(k\)，等到访问到\([4，5]\)的子节点时再传递下去。这样，线段树效率又得到了提高。
实现
干巴巴的说不知道大家能不能看懂。我们来看一下代码实现。
由于线段树是二叉树，我们直接规定\(i\)的儿子分别是\(2i\)和\(2i +1\)，具体原因相信大家在学习二叉树时都明白了。
通过define简化代码，\(x <<1\)和 \(x <<1｜1\)分别相当于x*2和x*2 + 1。
#define ls(x) (x << 1)
#define rs(x) (x << 1 | 1)
用结构体储存
struct Tree{
int l,r,sum，tag;
}tree[N*4];//N是数列长度,开4倍空间确保不会爆掉
通过push_up来在回溯后更新当前结点的值，用push_down向下传递懒标记。
void push_up(int p) {
t[p].w = t[ls(p)].w + t[rs(p)].w;
}
void push_down(int p){
t[ls(p)].w += t[p].tag * (t[ls(p)].r - t[ls(p)].l + 1);
t[rs(p)].w += t[p].tag * (t[rs(p)].r - t[rs(p)].l + 1);
t[ls(p)].tag += t[p].tag;
t[rs(p)].tag += t[p].tag;
t[p].tag = 0;
}
build函数的实现
void build(int p,int ll,int rr){ //p是当前所在的节点编号[ll,rr]是当前所处的区间
t[p].l = ll; t[p].r = rr;
if(ll == rr) { t[p].w = a[ll]; return;} //如果区间长度为1,t[p].sum显然等于a[ll];
int mid = (ll + rr) >> 1;//二分当前区间
build(ls(p),ll,mid); //处理左子树
build(rs(p),mid + 1,rr); //处理右子树
push_up(p); //处理完儿子，更新p节点的信息;
}
update函数的实现
void update(int p,int ll,int rr,int k){
if(ll <= t[p].l && t[p].r <= rr){
t[p].tag += k;
t[p].w += k * (t[p].r - t[p].l + 1);
return ;
}
int mid = (t[p].l + t[p].r) >> 1;
push_down(p);
if(ll <= mid) update(ls(p),ll,rr,k);
if(mid < rr) update(rs(p),ll,rr,k);
push_up(p);
}
query函数的实现
long long query(int p,int ll,int rr){
if(ll <= t[p].l && t[p].r <= rr)
return t[p].w;
int mid = (t[p].l + t[p].r) >> 1;
long long res = 0;
push_down(p);
if(ll <= mid) res += query(ls(p),ll,rr);
if(mid < rr) res += query(rs(p),ll,rr);
return res;
}
至此，一棵线段树就写好啦！
