P1312 Mayan游戏 [深搜][模拟]
题目描述
Mayan puzzle是最近流行起来的一个游戏。游戏界面是一个7 行5列的棋盘,上面堆放着一些方块,方块不能悬空堆放,即方块必须放在最下面一行,或者放在其他方块之上。游戏通关是指在规定的步数内消除所有的方块,消除方块的规则如下:
1 、每步移动可以且仅可以沿横向(即向左或向右)拖动某一方块一格:当拖动这一方块时,如果拖动后到达的位置(以下称目标位置)也有方块,那么这两个方块将交换位置(参见输入输出样例说明中的图6到图7 );如果目标位置上没有方块,那么被拖动的方块将从原来的竖列中抽出,并从目标位置上掉落(直到不悬空,参见下面图1 和图2);

2 、任一时刻,如果在一横行或者竖列上有连续三个或者三个以上相同颜色的方块,则它们将立即被消除(参见图1 到图3)。
注意:
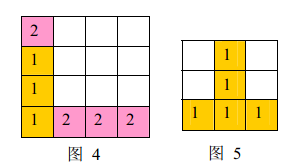
a) 如果同时有多组方块满足消除条件,几组方块会同时被消除(例如下面图4 ,三个颜色为1 的方块和三个颜色为 2 的方块会同时被消除,最后剩下一个颜色为 2的方块)。
b) 当出现行和列都满足消除条件且行列共享某个方块时,行和列上满足消除条件的所有方块会被同时消除(例如下面图5 所示的情形,5 个方块会同时被消除)。
3 、方块消除之后,消除位置之上的方块将掉落,掉落后可能会引起新的方块消除。注意:掉落的过程中将不会有方块的消除。
上面图1 到图 3 给出了在棋盘上移动一块方块之后棋盘的变化。棋盘的左下角方块的坐标为(0, 0 ),将位于(3, 3 )的方块向左移动之后,游戏界面从图 1 变成图 2 所示的状态,此时在一竖列上有连续三块颜色为4 的方块,满足消除条件,消除连续3 块颜色为4 的方块后,上方的颜色为3 的方块掉落,形成图 3 所示的局面。
输入格式
共 6 行。
第一行为一个正整数n,表示要求游戏通关的步数。
接下来的5行,描述 7×5 的游戏界面。每行若干个整数,每两个整数之间用一个空格隔开,每行以一个0 结束,自下向上表示每竖列方块的颜色编号(颜色不多于10种,从1开始顺序编号,相同数字表示相同颜色)。
输入数据保证初始棋盘中没有可以消除的方块。
输出格式
如果有解决方案,输出n行,每行包含 3 个整数x,y,g,表示一次移动,每两个整数之间用一个空格隔开,其中(x ,y)(x,y)表示要移动的方块的坐标,g 表示移动的方向,1 表示向右移动,-1表示向左移动。注意:多组解时,按照x为第一关健字,y为第二关健字,1 优先于−1 ,给出一组字典序最小的解。游戏界面左下角的坐标为(0 ,0)(0,0)。
如果没有解决方案,输出一行,包含一个整数-1−1。
做法
搜索+模拟。把各种操作写成一个个函数,简化代码。
数组说明:
m[i][j]---存图
cm[k][i][j]---存下搜索到cnt=k时的图,方便回溯
remove中的era[i][j]:若era[i][j] == 1,则m[i][j]可以消除。
函数:
remove:消除可以消除的方块
update:该落的方块落下来
move:交换两个方块,并完成接下来会发生的一切变化。
搜索:
要求字典序最小,1比-1优。我们考虑“左边的方块往右移”和“右边的方块往左移”时等效的。所以我们不需要考虑往左移。但要加一个判断:如果移动的格子没有方块,那么这个格子往右移在实际意义上说不通,所以这事要特判记录成“右边的方块往左移”。
具体看代码。
#include<bits/stdc++.h>
using namespace std;
int m[10][10],n,cm[10][10][10],Finished = 0,tot[10][3],num = -1;
void update(){
for(int i = 0; i < 5; ++i){
int space = 0;
for(int j = 0; j < 7; j++){
if(!m[i][j]) space++;
else{
if(!space)continue;
swap(m[i][j],m[i][j - space]);
}
}
}
}
bool remove(){
int era[10][10] = {0},flag = 0;
for(int i = 0; i < 5; i++)
for(int j = 0; j < 7; j++){
if(!m[i][j]) continue;
if(m[i][j] == m[i][j + 1] && m[i][j] == m[i][j - 1] && j != 0 && j != 6){
era[i][j] = era[i][j + 1] = era[i][j - 1] = 1;
flag = 1;
}
if(m[i][j] == m[i + 1][j] && m[i - 1][j] == m[i][j] && i != 0 && i != 4){
era[i][j] = era[i + 1][j] = era[i - 1][j] = 1;
flag = 1;
}
}
if(!flag) return 0;
for(int i = 0; i < 5; i++)
for(int j = 0; j < 7; j++){
if(era[i][j]) {
m[i][j] = 0;
}
}
return flag;
}
void move(int x,int y){
swap(m[x + 1][y],m[x][y]);
update();
while(remove()) update();
}
bool Is_Finished(){
for(int i = 0; i < 5; i++)
if(m[i][0]) return false;
return true;
}
void copy(int k){
for(int i = 0; i < 5; i++)
for(int j = 0; j < 7; j++)
cm[k][i][j] = m[i][j];
}
void paste(int k){
for(int i = 0; i < 5; i++)
for(int j = 0; j < 7; j++)
m[i][j] = cm[k][i][j];
}
void dfs(int cnt){
if(Is_Finished()) {
num = cnt;
Finished = 1;
for(int i = 0; i < num; i++)
cout << tot[i][0] << " " << tot[i][1] << " " << tot[i][2] << endl;
exit(0);
}
if(cnt == n) return;
copy(cnt);
if(Is_Finished()) { Finished = 1; num = cnt; return; }
for(int i = 0; i < 4; i++)
for(int j = 0; j < 7; j++){
if(!m[i][j] && !m[i + 1][j]) break;
if(m[i][j]){
tot[cnt][0] = i;
tot[cnt][1] = j;
tot[cnt][2] = 1;
}
else{
tot[cnt][0] = i + 1;
tot[cnt][1] = j;
tot[cnt][2] = -1;
}
move(i,j);
dfs(cnt + 1);
if(Finished) return;
paste(cnt);
}
}
int main(){
cin >> n;
for(int i = 0; i < 5; i++){
int x,tot = 0;
cin >> x;
while(x){
m[i][tot++] = x;
cin >> x;
}
}
dfs(0);
if(num == -1) cout << -1;
return 0;
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号