[自控]PID入门（二）初识pid算法

废话不多说直接承接上文

PID

三个字母分别是比例、积分、微分的缩写，他的公式也非常的简单，下面就是最常用的位置式pid的离散化公式了：

\[U(k)=K_perr(k)+K_i\Sigma err(k)\Delta t + K_d(err(k)-err(k-1))/\Delta t \]

在这个式子中,U(k)即pid的输出，Kp、Ki、Kd是三个常数，需要我们去整定，err(k)指的是第k次时期望值与输出值的差值。

当然直接看公式还是过于枯燥了，我们回到上文的例子。

回到那个栗子

由于pid是基于误差进行计算，我这里把昨天的图再进行一个改进：

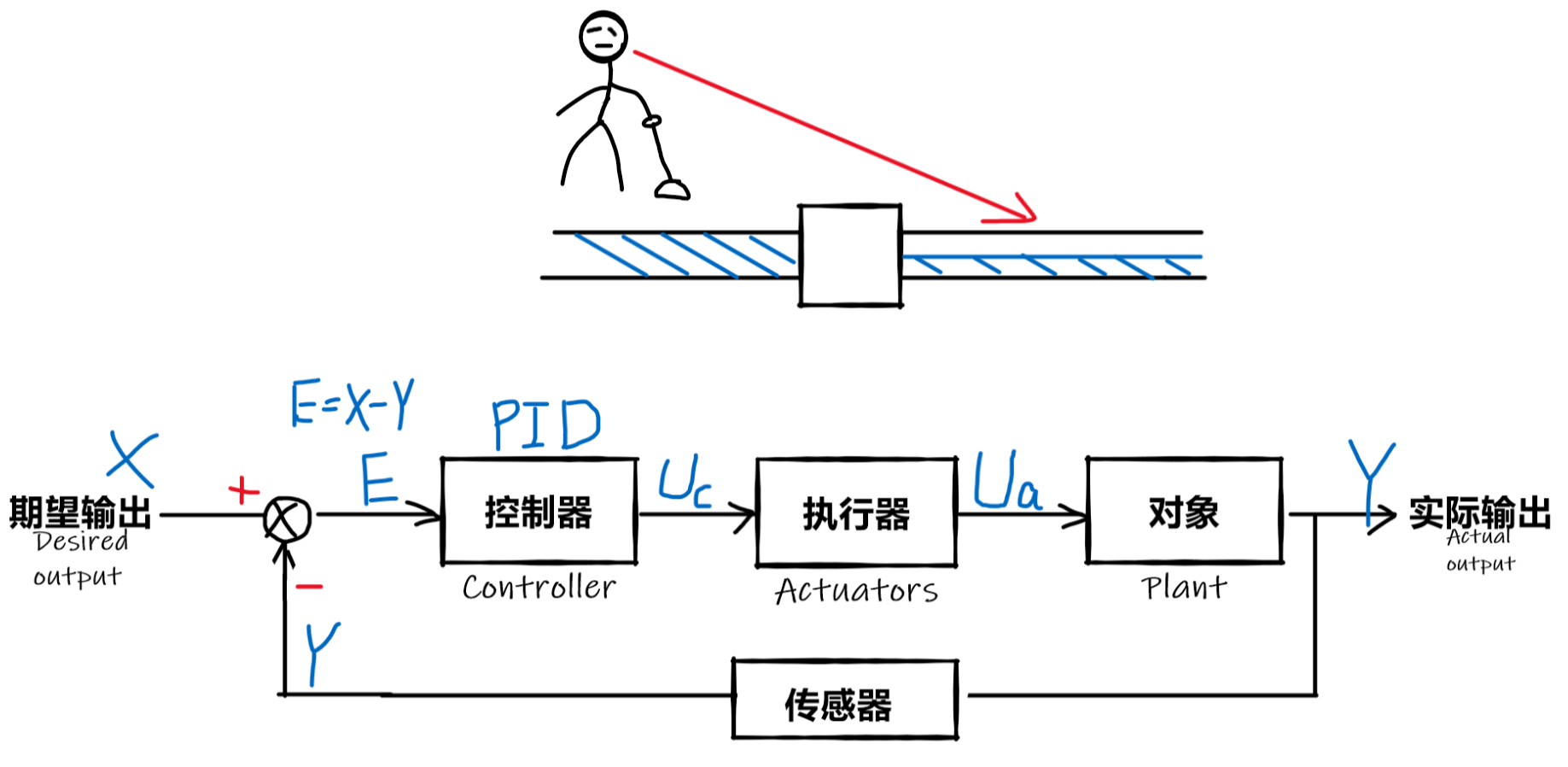
在图的左边，期望输出X减去实际输出Y获得的误差E来作为输入值给到PID控制器，然后再由PID去控制这个系统。

下面就分开来通俗的讲讲PID三个参数的运算到底是何意义

比例Proportional调节

在pid公式中我们来单看P项的输出：

\[K_pe \]

非常好理解，这里的小人看这个误差大不大，如果误差比较大，那可以把控制器的输出调大，等到误差小的时候我也相应地把输出调小，如果误差从正变成负了，那我也同样的把输出反过来。

积分Integral调节

同样的，我们把I项的输出拎出来：

\[K_i\Sigma e\Delta t \]

在小人这方面，我们可以这样理解：小人看见有误差，同时，误差存在的时间非常久，那就该把拉杆多拉动一些了。

不过单单这么说就不能体现I调节一些重要的作用了，这里我换一个例子：

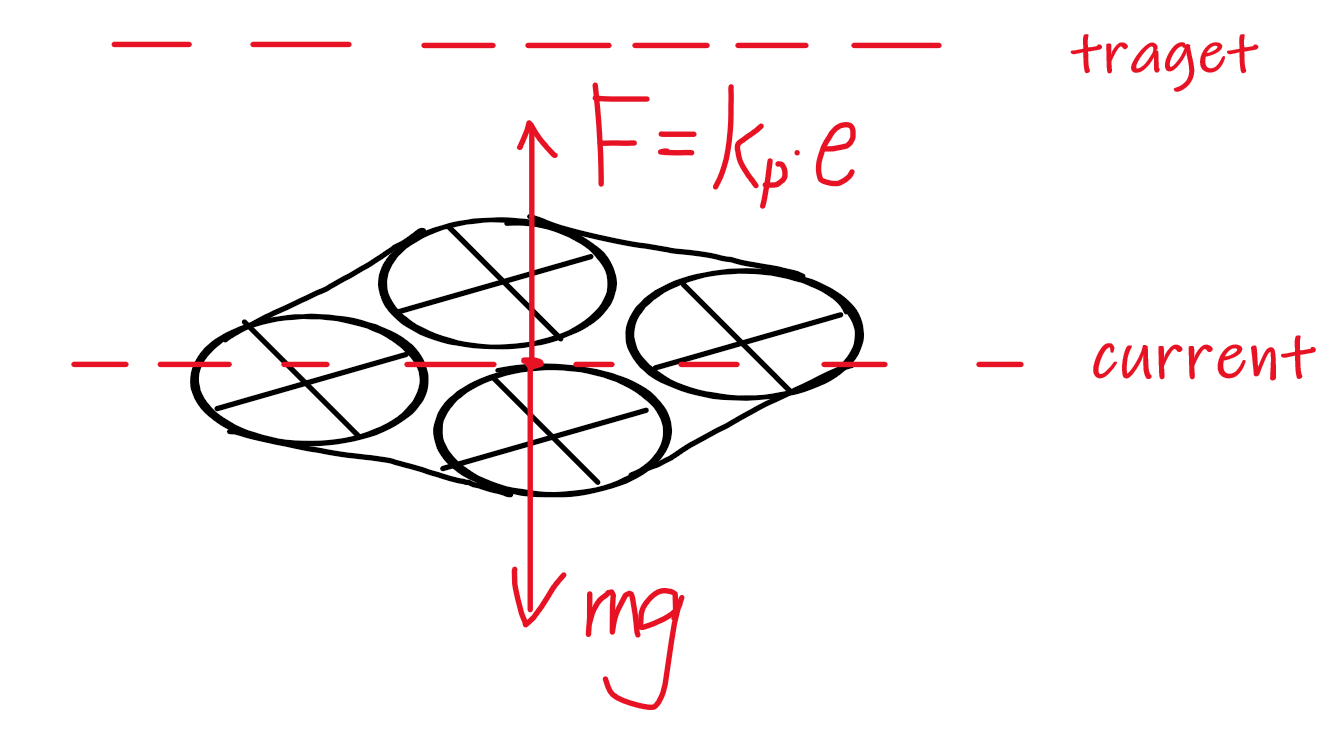
请大家把我画的这坨东西当作一个飞行器。这个时候它的任务是飞到target的高度，我们把pid的输出值简单当成飞行器的上升力，此时考虑如果我们只用P调节，那么我们会遇到一个问题，就是虽然始终有误差值，但是\(K_pe\)的值在我画的那条线上就已经等于重力了，再往上P调节的输出也完全无法满足让飞行器飞到指定高度。那么这个时候如果有I调节，我们将误差值进行积分，那我们就可以慢慢的把输出累积上去，最终就能达到目标值了。那么这就是积分项的一个消除稳态误差的效果。

微分Derivative调节

D项的输出：

\[K_d(err(k)-err(k-1))/\Delta t \]

相当于把误差对时间求导。
看误差的变化率有什么意思呢，其实它是一个提前抑制的作用，你会发现如果误差值持续减小的话那么D项的值也是小于零的，这里的小人发现误差变化过大了，实际的输出值很有可能会超出预期值，怎么办呢，那其实就可以通过D项来抑制输出，让他的变化率不那么大，最终可以平稳的从当前值达到目标值，有效的减少超调。