LeetCode 第 200 场周赛
罚时爆炸,呜呜呜
5475.统计好三元组
题目链接:5475.统计好三元组
给你一个整数数组 arr ,以及 a、b 、c 三个整数。请你统计其中好三元组的数量。
如果三元组 (arr[i], arr[j], arr[k]) 满足下列全部条件,则认为它是一个 好三元组 。
0 <= i < j < k < arr.length|arr[i] - arr[j]| <= a|arr[j] - arr[k]| <= b|arr[i] - arr[k]| <= c
其中 |x| 表示 x 的绝对值。
返回 好三元组的数量 。
示例 Sample
示例 1:
**输入:** arr = [3,0,1,1,9,7], a = 7, b = 2, c = 3
**输出:** 4
**解释:** 一共有 4 个好三元组:[(3,0,1), (3,0,1), (3,1,1), (0,1,1)] 。
示例 2:
**输入:** arr = [1,1,2,2,3], a = 0, b = 0, c = 1
**输出:** 0
**解释:** 不存在满足所有条件的三元组。
提示:
3 <= arr.length <= 1000 <= arr[i] <= 10000 <= a, b, c <= 1000
我的题解
模拟即可
class Solution {
public:
int countGoodTriplets(vector<int>& arr, int a, int b, int c) {
int ans(0);
for(int i = 0; i < arr.size(); i++)
for(int j = i + 1; j < arr.size(); j++)
for(int k = j + 1; k < arr.size(); k++) {
if(abs(arr[i] - arr[j]) <= a && abs(arr[j] - arr[k]) <= b && abs(arr[i] - arr[k]) <= c)
ans++;
}
return ans;
}
};
5476.找出数组游戏的赢家
题目链接:5476.找出数组游戏的赢家
给你一个由 不同 整数组成的整数数组 arr 和一个整数 k 。
每回合游戏都在数组的前两个元素(即 arr[0] 和 arr[1] )之间进行。比较 arr[0] 与 arr[1]
的大小,较大的整数将会取得这一回合的胜利并保留在位置 0 ,较小的整数移至数组的末尾。当一个整数赢得 k 个连续回合时,游戏结束,该整数就是比赛的
赢家 。
返回赢得比赛的整数。
题目数据 保证 游戏存在赢家。
示例 Sample
示例 1:
**输入:** arr = [2,1,3,5,4,6,7], k = 2
**输出:** 5
**解释:** 一起看一下本场游戏每回合的情况:
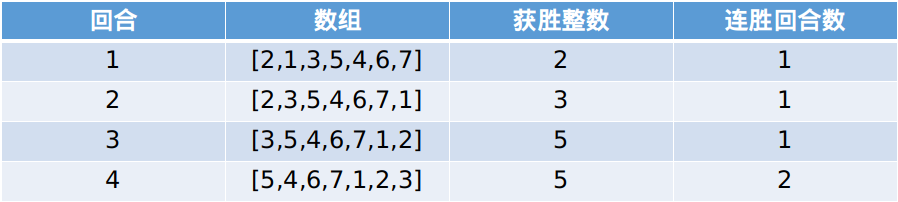
因此将进行 4 回合比赛,其中 5 是赢家,因为它连胜 2 回合。
示例 2:
**输入:** arr = [3,2,1], k = 10
**输出:** 3
**解释:** 3 将会在前 10 个回合中连续获胜。
示例 3:
**输入:** arr = [1,9,8,2,3,7,6,4,5], k = 7
**输出:** 9
示例 4:
**输入:** arr = [1,11,22,33,44,55,66,77,88,99], k = 1000000000
**输出:** 99
提示:
2 <= arr.length <= 10^51 <= arr[i] <= 10^6arr所含的整数 各不相同 。1 <= k <= 10^9
我的题解
class Solution {
public:
int getWinner(vector<int>& arr, const int k) {
int x = arr[0], c = 0;
for(int i = 1; i < arr.size(); i++) {
if(x > arr[i])
c++;
else
x = arr[i], c = 1;
if(c >= k)
return x;
}
return x;
}
};
5477.排布二进制网格的最少交换次数
题目链接:5477.排布二进制网格的最少交换次数
给你一个 n x n 的二进制网格 grid,每一次操作中,你可以选择网格的 相邻两行 进行交换。
一个符合要求的网格需要满足主对角线以上的格子全部都是 0 。
请你返回使网格满足要求的最少操作次数,如果无法使网格符合要求,请你返回 -1 。
主对角线指的是从 (1, 1) 到 (n, n) 的这些格子。
示例 Sample
示例 1:

**输入:** grid = [[0,0,1],[1,1,0],[1,0,0]]
**输出:** 3
示例 2:
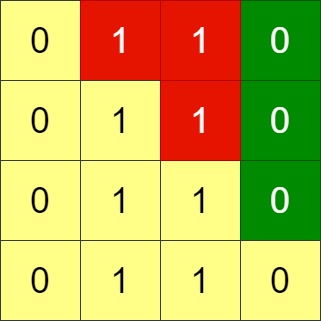
**输入:** grid = [[0,1,1,0],[0,1,1,0],[0,1,1,0],[0,1,1,0]]
**输出:** -1
**解释:** 所有行都是一样的,交换相邻行无法使网格符合要求。
示例 3:
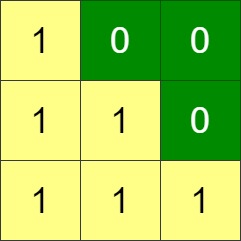
**输入:** grid = [[1,0,0],[1,1,0],[1,1,1]]
**输出:** 0
提示:
n == grid.lengthn == grid[i].length1 <= n <= 200grid[i][j]要么是0要么是1。
我的题解
预处理出每行末尾0的个数nums,对于位置i,选择合适的值即可,这里用的选择排序(交换用的冒泡,捂脸)。
class Solution {
public:
void gao(vector<int>&nums, int &ans) {
for(int i = 0, j, k; i < nums.size() - 1; i++) {
if(nums[i] < nums.size() - 1 - i) {
j = i + 1;
while(j < nums.size() && nums[j] < nums.size() - 1 - i)
j++;
if(j == nums.size())
return;
for(k = j; k > i; k--)
swap(nums[k], nums[k - 1]), ans++;
}
}
}
int minSwaps(vector<vector<int>>& grid) {
int ans(0);
vector<int>nums(grid.size(), 0);
for(int i = 0; i < nums.size(); i++) {
for(int j = grid[i].size() - 1; j >= 0; j--) {
if(grid[i][j] == 0)
nums[i]++;
else
break;
}
}
for(int i = 0; i <= nums.size(); i++) {
bool flag = true;
for(int j = 0; j < nums.size(); j++)
flag &= nums[j] >= nums.size() - 1 - j;
if(flag)
return ans;
gao(nums, ans);
}
return -1;
}
};
5478.最大得分
题目链接:5478.最大得分
你有两个 有序 且数组内元素互不相同的数组 nums1 和 nums2 。
一条 合法路径 定义如下:
- 选择数组 nums1 或者 nums2 开始遍历(从下标 0 处开始)。
- 从左到右遍历当前数组。
- 如果你遇到了
nums1和nums2中都存在的值,那么你可以切换路径到另一个数组对应数字处继续遍历(但在合法路径中重复数字只会被统计一次)。
得分定义为合法路径中不同数字的和。
请你返回所有可能合法路径中的最大得分。
由于答案可能很大,请你将它对 10^9 + 7 取余后返回。
示例 Sample
示例 1:
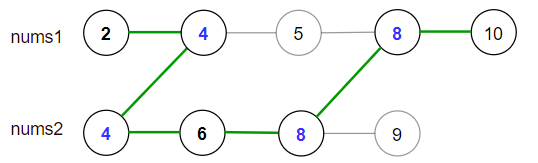
**输入:** nums1 = [2,4,5,8,10], nums2 = [4,6,8,9]
**输出:** 30
**解释:** 合法路径包括:
[2,4,5,8,10], [2,4,5,8,9], [2,4,6,8,9], [2,4,6,8,10],(从 nums1 开始遍历)
[4,6,8,9], [4,5,8,10], [4,5,8,9], [4,6,8,10] (从 nums2 开始遍历)
最大得分为上图中的绿色路径 **[2,4,6,8,10]** 。
示例 2:
**输入:** nums1 = [1,3,5,7,9], nums2 = [3,5,100]
**输出:** 109
**解释:** 最大得分由路径 **[1,3,5,100]** 得到。
示例 3:
**输入:** nums1 = [1,2,3,4,5], nums2 = [6,7,8,9,10]
**输出:** 40
**解释:** nums1 和 nums2 之间无相同数字。
最大得分由路径 **[6,7,8,9,10]** 得到。
示例 4:
**输入:** nums1 = [1,4,5,8,9,11,19], nums2 = [2,3,4,11,12]
**输出:** 61
提示:
1 <= nums1.length <= 10^51 <= nums2.length <= 10^51 <= nums1[i], nums2[i] <= 10^7nums1和nums2都是严格递增的数组。
我的题解
简单dp下就好,注意需要取模。
class Solution {
public:
int maxSum(vector<int>& nums1, vector<int>& nums2) const {
set<int>s;
long long ans(0);
const long long mod = 1e9 + 7;
for(int i : nums1)
s.insert(i), ans = max(ans, i * 1ll);
for(int i : nums2)
s.insert(i), ans = max(ans, i * 1ll);
vector<long long>dp(ans + 1);
int p(0), q(0);
for(int i : s) {
if(p < nums1.size() && nums1[p] == i) {
dp[i] = max(dp[i], (p == 0 ? 0 : dp[nums1[p - 1]]) + nums1[p]);
p++;
}
if(q < nums2.size() && nums2[q] == i) {
dp[i] = max(dp[i], (q == 0 ? 0 : dp[nums2[q - 1]]) + nums2[q]);
q++;
}
ans = max(ans, dp[i]);
}
return ans % mod;
}
};



