LeetCode-第 198 场周赛

第三题手速过慢，罚时爆炸，以至于第4题时间不足，赛后才写完ST预处理+二分答案。

5464.换酒问题

题目链接：5464.换酒问题

小区便利店正在促销，用 numExchange 个空酒瓶可以兑换一瓶新酒。你购入了 numBottles 瓶酒。

如果喝掉了酒瓶中的酒，那么酒瓶就会变成空的。

请你计算 最多 能喝到多少瓶酒。

样例输入与样例输出 Sample Input and Sample Output

示例 1：

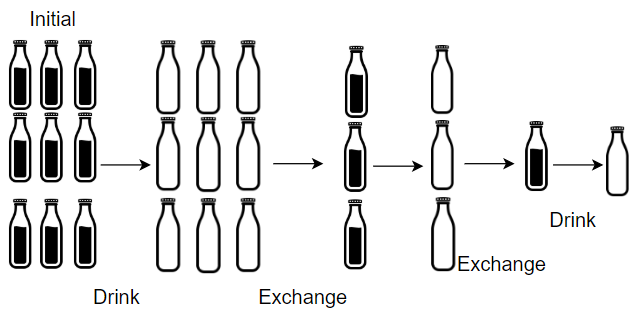
输入： numBottles = 9, numExchange = 3
输出： 13
解释： 你可以用 3 个空酒瓶兑换 1 瓶酒。
所以最多能喝到 9 + 3 + 1 = 13 瓶酒。

示例 2：

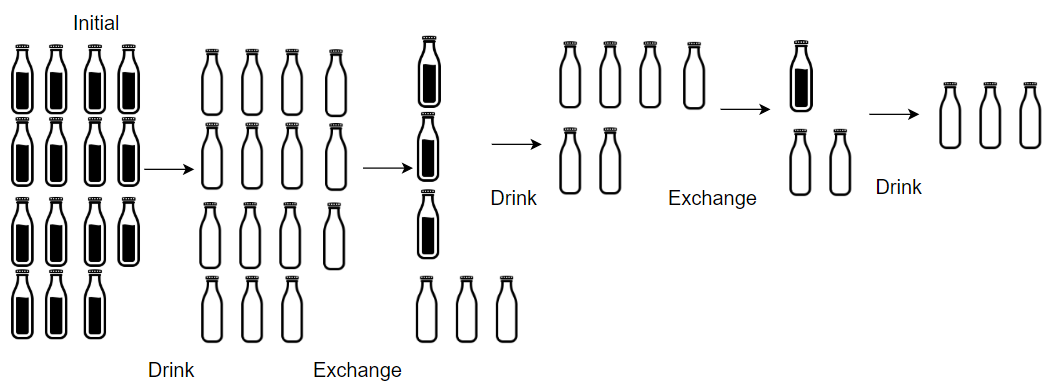
输入： numBottles = 15, numExchange = 4
输出： 19
解释： 你可以用 4 个空酒瓶兑换 1 瓶酒。
所以最多能喝到 15 + 3 + 1 = 19 瓶酒。

示例 3：

输入： numBottles = 5, numExchange = 5
输出： 6

示例 4：

输入： numBottles = 2, numExchange = 3
输出： 2

提示 Hint

提示：

• 1 <= numBottles <= 100
• 2 <= numExchange <= 100

题解

暴力模拟即可。

class Solution {
 public:
  int closestToTarget(vector<int>& arr, int target) {
    set<int>a[2];
    a[0].insert(INT_MAX);
    int ans(INT_MAX);
    for(int i = 0; i < arr.size(); ++i) {
      a[(i + 1) % 2].clear();
      for(int j : a[i % 2]) {
        a[(i + 1) % 2].insert(j & arr[i]);
        ans = min(ans, abs((j & arr[i]) - target));
      }
      a[(i + 1) % 2].insert(arr[i]);
      ans = min(ans, abs(arr[i] - target));
      a[i % 2].clear();
    }
    return ans;
  }
};

5465.子树中标签相同的节点数

题目链接：5465.子树中标签相同的节点数

给你一棵树（即，一个连通的无环无向图），这棵树由编号从 0 到 n - 1 的 n 个节点组成，且恰好有 n - 1 条 edges
。树的根节点为节点 0 ，树上的每一个节点都有一个标签，也就是字符串 labels 中的一个小写字符（编号为 i 的 节点的标签就是
labels[i] ）

边数组 edges 以 edges[i] = [ai, bi] 的形式给出，该格式表示节点 ai 和 bi 之间存在一条边。

返回一个大小为 n 的数组，其中 ans[i] 表示第 i 个节点的子树中与节点 i 标签相同的节点数。

树 T 中的子树是由 T 中的某个节点及其所有后代节点组成的树。

样例输入与样例输出 Sample Input and Sample Output

示例 1：

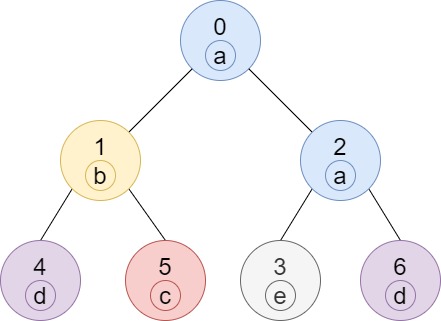
输入： n = 7, edges = [[0,1],[0,2],[1,4],[1,5],[2,3],[2,6]], labels = "abaedcd"
输出： [2,1,1,1,1,1,1]
解释： 节点 0 的标签为 'a' ，以 'a' 为根节点的子树中，节点 2 的标签也是 'a' ，因此答案为 2 。注意树中的每个节点都是这棵子树的一部分。
节点 1 的标签为 'b' ，节点 1 的子树包含节点 1、4 和 5，但是节点 4、5 的标签与节点 1 不同，故而答案为 1（即，该节点本身）。

示例 2：

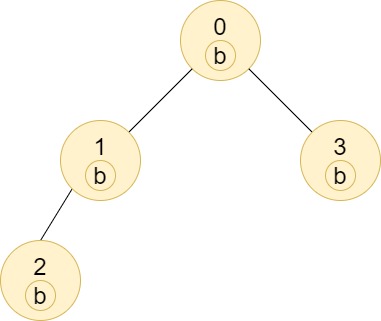
输入： n = 4, edges = [[0,1],[1,2],[0,3]], labels = "bbbb"
输出： [4,2,1,1]
解释： 节点 2 的子树中只有节点 2 ，所以答案为 1 。
节点 3 的子树中只有节点 3 ，所以答案为 1 。
节点 1 的子树中包含节点 1 和 2 ，标签都是 'b' ，因此答案为 2 。
节点 0 的子树中包含节点 0、1、2 和 3，标签都是 'b'，因此答案为 4 。

示例 3：

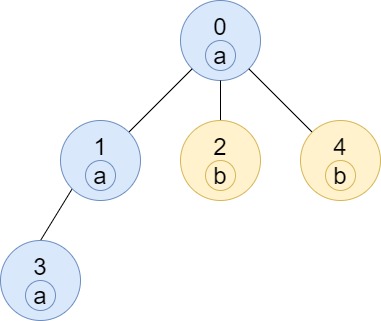
输入： n = 5, edges = [[0,1],[0,2],[1,3],[0,4]], labels = "aabab"
输出： [3,2,1,1,1]

示例 4：

输入： n = 6, edges = [[0,1],[0,2],[1,3],[3,4],[4,5]], labels = "cbabaa"
输出： [1,2,1,1,2,1]

示例 5：

输入： n = 7, edges = [[0,1],[1,2],[2,3],[3,4],[4,5],[5,6]], labels = "aaabaaa"
输出： [6,5,4,1,3,2,1]

提示 Hint

提示：

• 1 <= n <= 10^5
• edges.length == n - 1
• edges[i].length == 2
• 0 <= ai, bi < n
• ai != bi
• labels.length == n
• labels 仅由小写英文字母组成

题解

DFS 遍历即可。

class Solution {
 public:
  vector<int> DFS(int root, int fa, vector<int>&ans, const vector<vector<int>>&g, const string &labels) {
    vector<int>cnt(26, 0);
    cnt[labels[root] - 'a']++;
    for(int v : g[root]) {
      if(v == fa)
        continue;
      vector<int>delta = DFS(v, root, ans, g, labels);
      for(int j = 0; j < 26; ++j)
        cnt[j] += delta[j];
    }
    ans[root] = cnt[labels[root] - 'a'];
    return cnt;
  }

  vector<int> countSubTrees(int n, vector<vector<int>>& edges, string labels) {
    if(n == 0)
      return {};
    vector<int>ans(n);
    vector<vector<int>>g(n);
    for(vector<int>edge : edges) {
      g[edge[0]].push_back(edge[1]);
      g[edge[1]].push_back(edge[0]);
    }
    DFS(0, -1, ans, g, labels);
    return ans;
  }
};

5466.最多的不重叠子字符串

题目链接：5466.最多的不重叠子字符串

给你一个只包含小写字母的字符串 s ，你需要找到 s 中最多数目的非空子字符串，满足如下条件：

1. 这些字符串之间互不重叠，也就是说对于任意两个子字符串 s[i..j] 和 s[k..l] ，要么 j < k 要么 i > l 。
2. 如果一个子字符串包含字符 c ，那么 s 中所有 c 字符都应该在这个子字符串中。

请你找到满足上述条件的最多子字符串数目。如果有多个解法有相同的子字符串数目，请返回这些子字符串总长度最小的一个解。可以证明最小总长度解是唯一的。

请注意，你可以以 任意 顺序返回最优解的子字符串。

样例输入与样例输出 Sample Input and Sample Output

示例 1：

输入： s = "adefaddaccc"
输出： ["e","f","ccc"]
解释： 下面为所有满足第二个条件的子字符串：
[
"adefaddaccc"
"adefadda",
"ef",
"e",
"f",
"ccc",
]
如果我们选择第一个字符串，那么我们无法再选择其他任何字符串，所以答案为 1 。如果我们选择 "adefadda" ，剩下子字符串中我们只可以选择 "ccc" ，它是唯一不重叠的子字符串，所以答案为 2 。同时我们可以发现，选择 "ef" 不是最优的，因为它可以被拆分成 2 个子字符串。所以最优解是选择 ["e","f","ccc"] ，答案为 3 。不存在别的相同数目子字符串解。

示例 2：

输入： s = "abbaccd"
输出： ["d","bb","cc"]
解释： 注意到解 ["d","abba","cc"] 答案也为 3 ，但它不是最优解，因为它的总长度更长。

提示 Hint

提示：

• 1 <= s.length <= 10^5
• s 只包含小写英文字母。

题解

找到所有子串，排序（短的优先），能加则加。

typedef pair<int, int>PII;

class Solution {
 public:
  vector<string> maxNumOfSubstrings(string s) {
    if(s.length() == 0)
      return {};
    vector<PII>st;
    vector<int>first_pos(26, -1), last_pos(26, -1);
    for(int i = 0; i < 26; ++i) {
      first_pos[i] = s.find_first_of('a' + i);
      last_pos[i] = s.find_last_of('a' + i);
    }
    for(int i = 0; i < 26; ++i) {
      size_t b = s.find_first_of('a' + i);
      size_t e = s.find_last_of('a' + i);
      if(b == string::npos)
        continue;
      for(bool redo = true; redo;) {
        redo = false;
        for(int j = b; j <= e; j++)
          if(e < last_pos[s[j] - 'a'])
            e = last_pos[s[j] - 'a'];
          else if(b > first_pos[s[j] - 'a'])
            b = first_pos[s[j] - 'a'], redo = true;
      }
      st.push_back({e - b + 1, b});
    }
    sort(st.begin(), st.end());
    vector<bool>vis(s.length(), false);
    vector<string>ans;
    for(PII p : st) {
      bool v = false;
      for(int j = p.second; j < p.second + p.first; j++) {
        if(vis[j]) {
          v = true;
          break;
        }
      }
      if(v)
        continue;
      ans.push_back(s.substr(p.second, p.first));
      for(int j = p.second; j < p.second + p.first; j++)
        vis[j] = true;
    }
    return ans;
  }
};

5467.找到最接近目标值的函数值

题目链接：5467.找到最接近目标值的函数值

Winston 构造了一个如上所示的函数 func 。他有一个整数数组 arr 和一个整数 target ，他想找到让 |func(arr, l, r) - target| 最小的 l 和 r 。

请你返回 |func(arr, l, r) - target| 的最小值。

请注意， func 的输入参数 l 和 r 需要满足 0 <= l, r < arr.length 。

样例输入与样例输出 Sample Input and Sample Output

示例 1：

输入： arr = [9,12,3,7,15], target = 5
输出： 2
解释： 所有可能的 [l,r] 数对包括 [[0,0],[1,1],[2,2],[3,3],[4,4],[0,1],[1,2],[2,3],[3,4],[0,2],[1,3],[2,4],[0,3],[1,4],[0,4]]， Winston 得到的相应结果为 [9,12,3,7,15,8,0,3,7,0,0,3,0,0,0] 。最接近 5 的值是 7 和 3，所以最小差值为 2 。

示例 2：

输入： arr = [1000000,1000000,1000000], target = 1
输出： 999999
解释： Winston 输入函数的所有可能 [l,r] 数对得到的函数值都为 1000000 ，所以最小差值为 999999 。

示例 3：

输入： arr = [1,2,4,8,16], target = 0
输出： 0

提示 Hint

提示：

• 1 <= arr.length <= 10^5
• 1 <= arr[i] <= 10^6
• 0 <= target <= 10^7

题解

法1.简单的ST表(倍增解决RMQ问题的那个算法)预处理+二分答案

class Solution {
 public:
  int gao(vector<vector<int>>&d, int x, int y)const {
    int k = log2(y - x + 1);
    int ret = d[x][k] & d[y - (1 << k) + 1][k];
    return ret;
  }

  int closestToTarget(vector<int>& arr, int target) {
    int len = arr.size();
    vector<vector<int>>d(len, vector<int>(20));
    for(int i = 0; i < len; ++i)
      d[i][0] = arr[i];
    for(int j = 1; j <= log2(len); ++j) {
      for(int i = 0; i + (1 << j) - 1 < len; ++i) {
        d[i][j] = d[i][j - 1] & d[i + (1 << (j - 1))][j - 1];
      }
    }
    int ans(0x7ffffff);
    for(int i = 0; i < len; ++i) {
      if(i && arr[i] == arr[i - 1])
        continue;
      int l = i, r = len - 1, mid;
      if(gao(d, i, r) < target)
        while(l < r) {
          //cout<< l << " " << r<<endl;
          mid = (l + r) >> 1;
          if(gao(d, i, mid) > target)
            l = mid + 1;
          else
            r = mid;
        } else
        l = r;
      ans = min(ans, abs(gao(d, i, l) - target));
      if(l - 1 >= i)
        ans = min(ans, abs(gao(d, i, l - 1) - target));
    }
    return ans;
  }
};

法2.暴力优化。对于每个以 \(i\) 位置结尾的，用 set 去重，可用滚动数组的方式简单优化下。(有题解是用 vector 然后 unique erase)
set 的大小最多就 \(20\) ，以 arr[i] 结尾，则每次变动一位，最多 \(20\) 位 (\(1e6 \approx 2^{20}\))。

class Solution {
 public:
  int closestToTarget(vector<int>& arr, int target) {
    set<int>a[2];
    a[0].insert(INT_MAX);
    int ans(INT_MAX);
    for(int i = 0; i < arr.size(); ++i) {
      a[(i + 1) % 2].clear();
      for(int j : a[i % 2]) {
        a[(i + 1) % 2].insert(j & arr[i]);
        ans = min(ans, abs((j & arr[i]) - target));
      }
      a[(i + 1) % 2].insert(arr[i]);
      ans = min(ans, abs(arr[i] - target));
      a[i % 2].clear();
    }
    return ans;
  }
};