统计学基础
获取数据:
内部数据和外部数据:内部数据比外部数据可靠
一手数据和二手数据:一手数据比二手数据可靠
抽样方法:
概率抽样,例如调查某大学学生跑1000米的成绩
- 简单随机抽样:去学校随机调查看到的学生
- 分层抽样:对大一、大二、大三、大四各选取一定数量的学生进行调查
- 整群抽样:不区分性别,需要对男生和女生都进行调查
- 系统抽样(等距抽样):按照一定规则对学号进行抽样,
非概率抽样,主要适用于所需调查的问题不具有普遍性,例如调查某大学学生每周阅读英文杂志的时长
- 方便抽样:研究者选取自己熟悉的人进行调查
- 判断抽样:研究者根据自己的判断决定是否对偶一个人进行调查
- 自愿抽样:被研究者自愿参与调查,自愿抽样在遇到敏感问题时往往会收到比较极端的结果
- 滚雪球抽样:选取到被调查者,被调查者再推荐满足条件的人参与调查
数据误差
- 抽样误差
- 非抽样误差:抽样框误差、回答误差、非回答误差、调查员误差等
Z score标准化
z=(x-μ)/σ,其中x为某一具体数,μ为平均数,σ为标准差
描述统计
集中趋势:平均数、中位数、众数
离散趋势:极值、四分位差
正态分布
若随机变量X服从一个数学期望为μ、方差为σ^2的正态分布,记为N(μ,σ^2),其概率密度函数为正态分布,期望值μ决定了其位置,标准差σ决定了分布的幅度。当μ = 0、σ = 1时的正态分布是标准正态分布,且 (X-μ)/σ 服从标准正态分布N(0,1)。
根据经验,距均值竖线左右两侧分别1个标准差的竖线,与正太曲线和横坐标轴围起来的面积约为整体面积的68%。
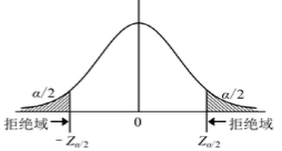
如果X1和X2为两个独立的满足正态分布的样本,则有如下结论。
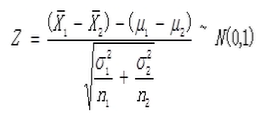
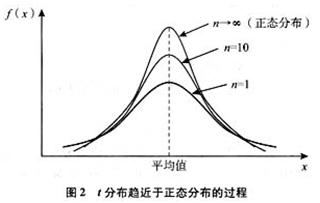
t分布
t-分布(t-distribution)用于根据小样本来估计呈正态分布且方差未知的总体的均值。t分布曲线形态与与自由度df有关,与标准正态分布曲线相比自由度df越小,t分布曲线愈平坦,中间愈低双侧尾部翘得愈高;自由度df愈大,t分布曲线愈接近正态分布曲线;当自由度df=∞时,t分布曲线为标准正态分布曲线,一般为30时从生成的图表上来看基本重合。

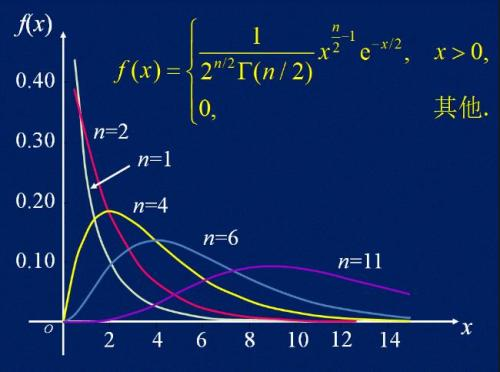
卡方分布
若n个相互独立的随机变量ξ₁,ξ₂,...,ξn服从标准正态分布(也称独立同分布于标准正态分布),则这n个随机变量的平方和构成一组新的随机变量,其分布规律称为卡方分布(chi-square distribution),ξ~x2(n)。由于平方过所以卡方分布的值不会小于0.
F分布
若总体X~N(0,1),(X1,X2,...,Xn1)与(Y1,Y2,...,Yn2)为来自X的两个独立样本,即x~x2(n1),y~x2(n2),设统计量F=(x/n1)/(y/n2),则统计量F服从自由度n1和n2的F 分布,记为F~F(n1,n2)

点估计和区间估计
区间估计为[样本均值-一定置信水平下置信度,样本均值+一定置信水平下置信度]
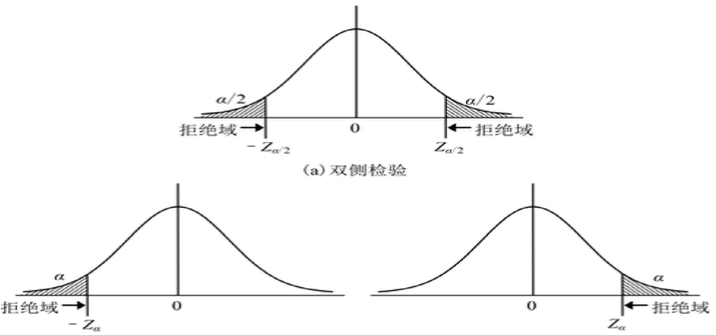
假设检验前提:总体符合正太分布
假设检验原理:
H0:μ=100
H1:μ≠100
对统计样本进行检验,如果P>显著性水平α→H0,P<显著性水平α→H0
单因素方差分析
假设检验原理:
H0:xx因素不影响因变量
H1:xx因素影响因变量
几个概念(xij表示样本值,x拔表示每组的样本均值,x拔拔表示所有样本均值,n表示样本数量,k表示组数,)
组内平方和 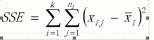
组内均方和 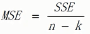
总平方和 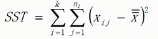
组间平方和 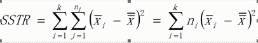
组间均方 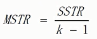
单因素方差分析F值计算 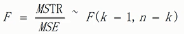
推导SST = SSE + SSTR,即总平方和=组内平方和+组间平方和
DFsst = DFSSE + DFSSTR
无交互因素双因素方差分析
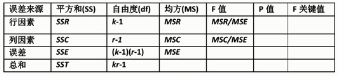
假设检验原理(2套):
H0:行因素不影响因变量(set1)
H1:行因素显著影响因变量(set1)
H0:列因素不影响因变量(set2)
H1:列因素显著影响因变量(set2)
双因素交互作用
假设检验原理:
H0:行因素和列因素互相独立,无交互作用
H1:行因素和列因素互相影响,有交互作用
线性回归
一元线性回归:一个自变量与因变量的线性关系,形如y = a + bx + e
多元线性回归:多个自变量与因变量的线性关系,形如y = a + b1x1 + b2x2 + ··· + bnxn + e
R square表示因变量有多少可以由自变量解释
对于多元线性回归,即使某一因素对因变量的解释能力很弱,但是如果将其加入模型R2仍然会增加,这就可能会出现虽然R2很高,但其实模型中有一些不太相关的自变量,为了解决这个问题引入了调整R square的概念,Ra2与R2的关系如下,随着R2的增大而增大,随着因变量个数的增加而减小。
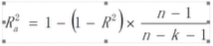


 浙公网安备 33010602011771号
浙公网安备 33010602011771号