无监督学习-主成分分析和聚类分析

聚类分析（cluster analysis）是将一组研究对象分为相对同质的群组（clusters）的统计分析技术，即将观测对象的群体按照相似性和相异性进行不同群组的划分，划分后每个群组内部各对象相似度很高，而不同群组之间的对象彼此相异度很高。

回归、分类、聚类的区别 ：

• 有监督学习 --->> 回归、分类    /   无监督学习  --->>聚类
• 回归 -->>产生连续结果，可用于预测
• 分类 -->>产生连续结果，可用于预测
• 聚类 -->>产生一组集合，可用于降维

一、PCA主成分分析

 

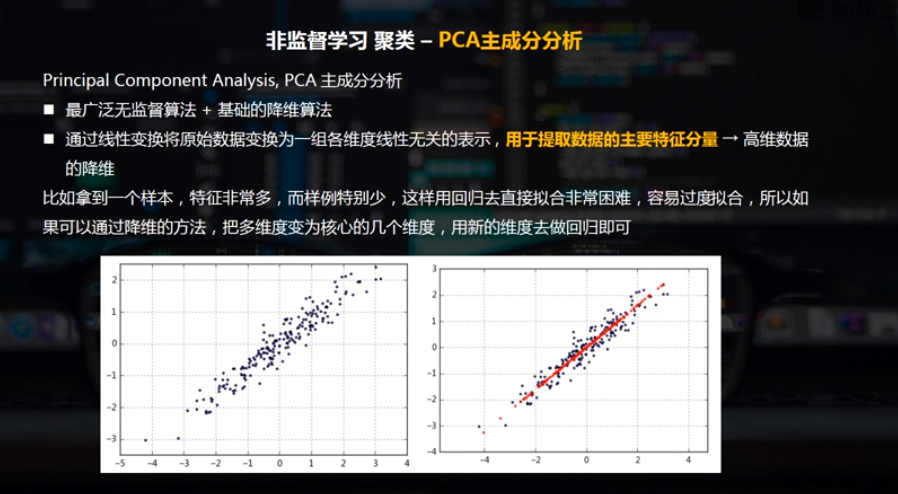
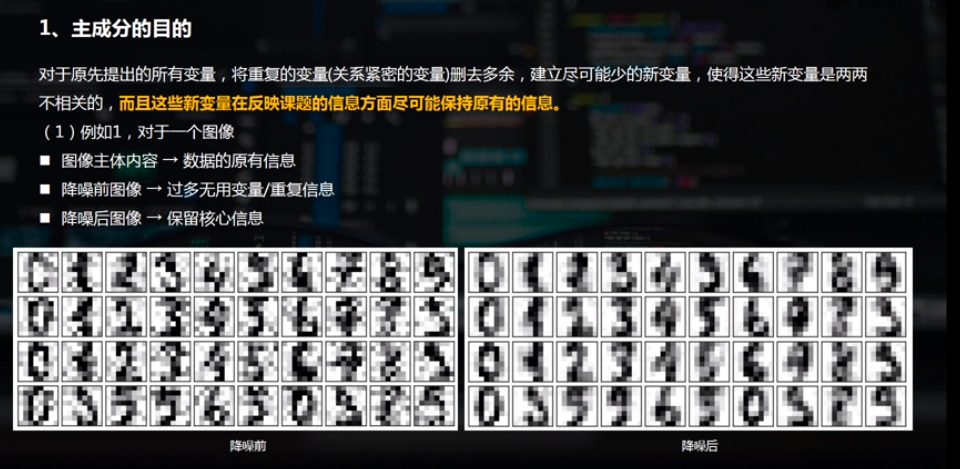
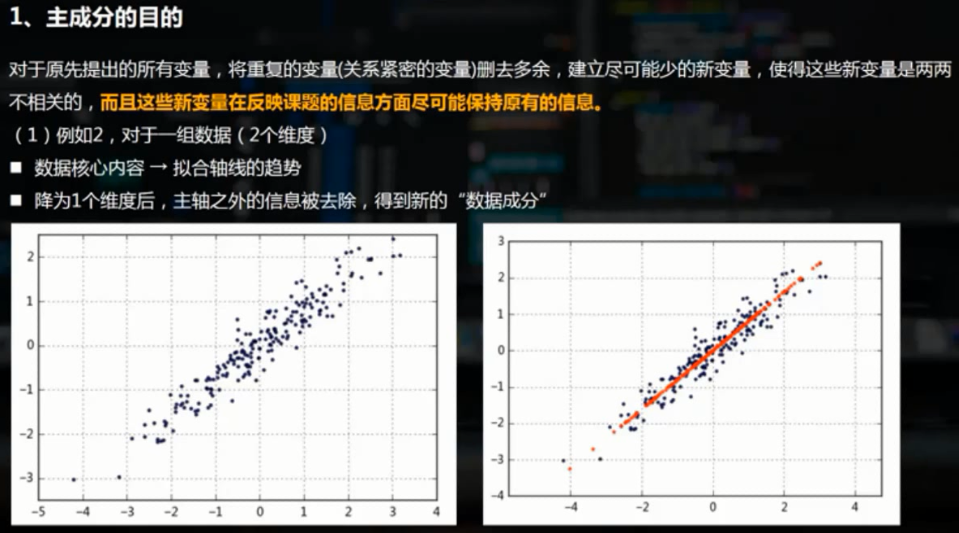
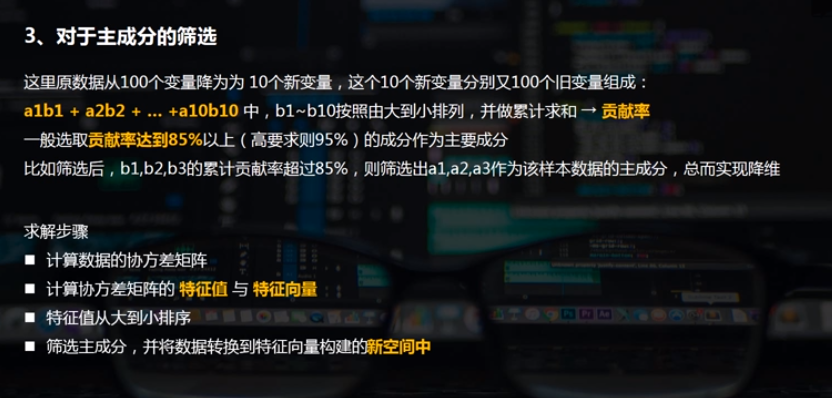
二、PCA主成分的python实现方法

通过sklearn的PCA类实现，from sklearn.decomposition import PCA

pca = PCA(n_components=1) # n_components参数表示最终维度

pca.fit(data) #创建模型

data_pca = pca.transform(data) #降维，创建模型和降维可通过一步实现fit_transform

data_inverse = pca.inverse_transform(data_pca) #根据降维结果反算原始数据

1.二维数据降维

rng = np.random.RandomState(8)
data = np.dot(rng.rand(2,2),rng.randn(2,200)).T  #矩阵相乘
df = pd.DataFrame({'X1':data[:,0],'X2':data[:,1]})
print(df.shape)
print(df.head())
plt.scatter(df['X1'],df['X2'],alpha = 0.8,marker = '.')
plt.axis('equal')  #坐标轴每个单位表示的刻度相同
# (200, 2)
#          X1        X2
# 0 -1.174787 -1.404131
# 1 -1.374449 -1.294660
# 2 -2.316007 -2.166109
# 3  0.947847  1.460480
# 4  1.762375  1.640622

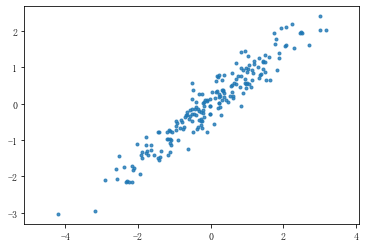
from sklearn.decomposition import PCA
pca = PCA(n_components=1) # n_components参数表示最终维度
pca.fit(df)
print(pca.explained_variance_)
print(pca.components_)
# print(pca.n_components) #返回保留的成分个数
# print(pca.explained_variance_ratio_) 
# 结果降为几个维度，就有几个特征值；原始数据有几个维度，就有几个特征向量
# explained_variance_：特征值
# components_：返回具有最大方差的成分，即特征向量

# 这里是shape(200,2)降为shape(200,1)，只有1个特征值，对应2个特征向量
# 降维后主成分 A1 = 0.7788006 * X1 + 0.62727158 * X2
# 成分的结果值 = 2.80 * （-0.77*x1 -0.62 * x2） #通过这个来筛选它的主成分

df_pca = pca.transform(df)  # 数据转换，将原始二维数据转换为降维后的一维数据
df_inverse = pca.inverse_transform(df_pca)  # 数据转换，将降维后的一维数据转换成原始的二维数据
print('original shape:',df.shape)
print('transformed shape:',df_pca.shape)
print(df.head(10))
print(df_pca[:10])
print(df_inverse[:10])

plt.scatter(df['X1'],df['X2'], alpha = 0.8, marker = '.') #原始数据散点；
plt.scatter(x_inverse[:,0],x_inverse[:,1], alpha = 0.8, marker = '.',color = 'r') #转换之后的散点，红色的就是最后的特征数据
plt.axis('equal')

2.多维数据降维

 多维数据降维，使用自带的图像数据进行测试。

from sklearn.datasets import load_digits
digits = load_digits()
print(type(digits))
print(digits.data[:2])
print('数据长度为:%i条' % len(digits['data']))
print('数据形状为：',digits.data.shape) #总共1797条数据，每条数据有64个变量
print('字段：',digits.keys())
print('分类(数值)：',digits.target)
print('分类(名称)：',digits.target_names)

 

将上述数据由64维降为2维，降维后的2个维度肯定都是主成分。

pca = PCA(n_components=2)  #降为2维
projected = pca.fit_transform(digits.data)  #相当于先fit构建模型，再transform进行转换
projected[:2]
print('original shape:',digits.data.shape)
print('transformed shape:',projected.shape)
print('特征值',pca.explained_variance_)  #2个特征值
print('特征向量',pca.components_.shape) #2个成分，每个成分都有64个特征向量

# original shape: (1797, 64)
# transformed shape: (1797, 2)
# 特征值 [179.0069301  163.71774688]
# 特征向量 (2, 64)

plt.scatter(projected[:,0],projected[:,1],s = 10,c = digits.target, cmap='Reds',edgecolor = 'none',alpha = 0.5)
plt.colorbar()

 

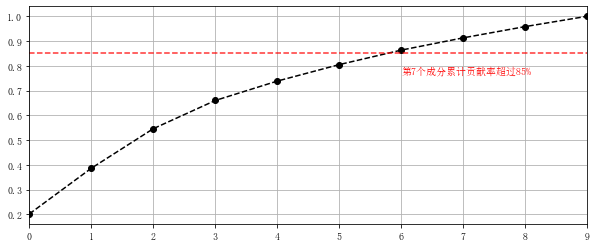
将上述数据降为10维，并求主要成分。

pca = PCA(n_components=10)  #降为10维
projected = pca.fit_transform(digits.data)  #相当于先fit构建模型，再transform进行转换
projected[:2]
print('original shape:',digits.data.shape)
print('transformed shape:',projected.shape)
print(pca.explained_variance_)  # 输出特征值 ；10个特征值
print(pca.components_.shape)  # 输出特征向量形状

s = pca.explained_variance_
c_s = pd.DataFrame({'x':s,'x_cumsum':s.cumsum()/s.sum()})
print(c_s)
c_s['x_cumsum'].plot(style = '--ko', figsize = (10,4))
plt.axhline(0.85,color='r',linestyle="--",alpha=0.8)  
plt.text(6,c_s['x_cumsum'].iloc[6]-0.1,'第7个成分累计贡献率超过85%',color = 'r')
plt.grid()

   

 

三、K-means聚类的python实现方法

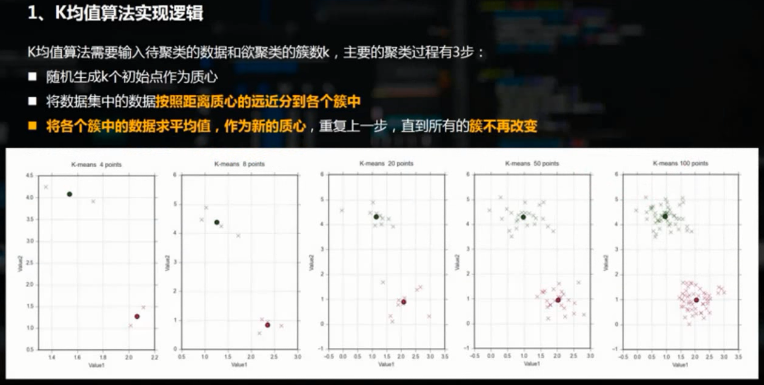
K-means聚类是最常用的机器学习聚类算法，且为典型的基于距离的聚类算法。主要步骤为：

kmeans = KMeans(n_clusters=4) #创建模型

kmeans.fit(x) #导入数据

y_kmeans = kmeans.predict(x) #预测每个数据属于哪个类

centroids = kmeans.cluster_centers_ #每个类的中心点

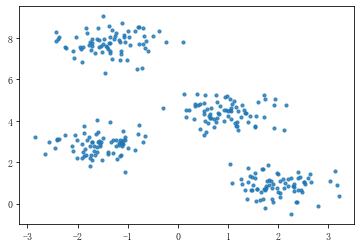
 先使用sklearn自带的生成器生成数据

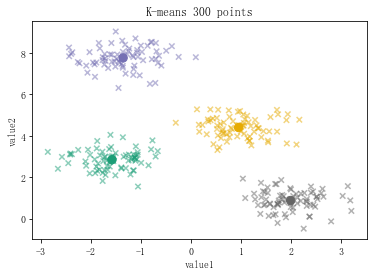
from sklearn.datasets.samples_generator import make_blobs  # make_blobs聚类数据生成器
x,y_true = make_blobs(n_samples=300,centers=4,cluster_std=0.5,random_state=0)
print(x[:5])
print(y_true[:5])

# n_samples 生成的样本总数
# centers 类别数
# cluster_std 每个类别的方差，如果多类数据不同方差可设置为[std1,std2,...stdn]
# random_state 随机数种子
# x 生成的数据，y 数据对应的类别
# n_features 每个样本的特征数

plt.scatter(x[:,0],x[:,1],s=10,alpha=0.8)

   

通过sklearn的KMeans进行聚类分析

from sklearn.cluster import KMeans
kmeans = KMeans(n_clusters=4)  #创建模型
kmeans.fit(x)  #导入数据
y_kmeans = kmeans.predict(x)  #预测每个数据属于哪个类
centroids = kmeans.cluster_centers_ #每个类的中心点
plt.scatter(x[:,0],x[:,1],s=30,c=y_kmeans,cmap = 'Dark2',alpha=0.5,marker='x')
plt.scatter(centroids[:,0],centroids[:,1],s=70,c=[0,1,2,3],cmap = 'Dark2',marker='o')
plt.title('K-means 300 points')
plt.xlabel('value1')
plt.ylabel('value2')