监督学习-回归分析
一、数学建模概述

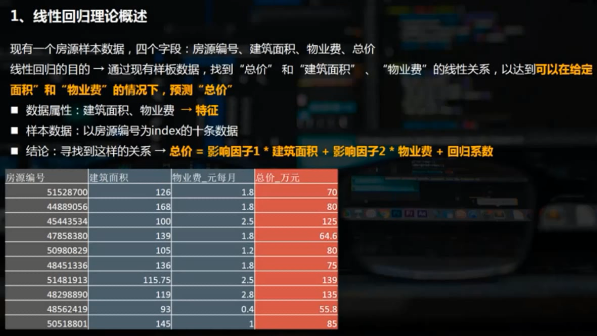
监督学习:通过已有的训练样本进行训练得到一个最优模型,再利用这个模型将所有的输入映射为相应的输出。监督学习根据输出数据又分为回归问题(regression)和分类问题(classfication),回归问题的输出通常是连续的数值,分类问题的输出通常是几个特定的数值。
非监督学习:根据类别未知的训练样本,解决模式识别中的各种问题,主要为聚类问题(cluster analysis)。
二、回归分析概述
在统计学中,回归分析(regression analysis)指的是确定两种或两种以上变量间互相依赖的定量关系的一种统计分析方法。
根据自变量和因变量之间的关系类型,可分为线性回归分析和非线性回归分析。
线性回归linear analys
线性回归通常是学习预测模型时首选的技术之一。在线性回归中,因变量是连续的,而自变量可以是连续的的也可以是离散的,回归线的性质是线性的。
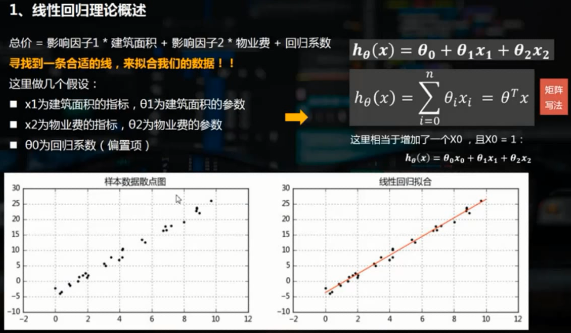
线性回归使用最佳的拟合直线(即回归线)在因变量y和一个或多个自变量x之间建立一种关系,简单线性回归(一元线性回归)可表示为y=a+b*x
多元线性回归可表示为y=a+b1*x1+b2*x2。线性回归可以根据给定的预测变量s来预测目标变量的值。


三、使用python实现线性回归分析
需要先安装sklearn模块,并导入其中的线性回归类from sklearn.linear_model import LinearRegression
model = LinearRegression() 创建模型
model.fit(x,y) 将样本导入模型,x需要是列变量
print('斜率和截距分别为:',model.coef_,model.intercept_)
y_pre = model.predict(x_pre) 通过模型预测给定的自变量对应的因变量
1.一元线性回归
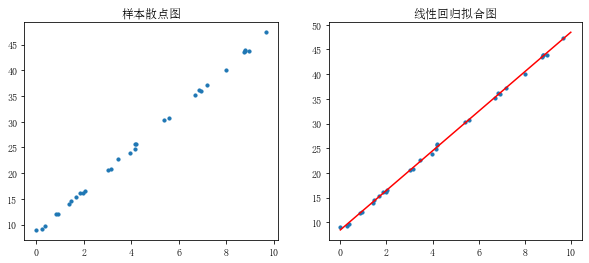
rng = np.random.RandomState(1) #生成随机数种子,种子相同每次生成的随机数相同 x = 10 * rng.rand(30) #通过随机数种子生成随机数 y = 8 + 4 * x + rng.rand(30) # rng.rand(30)表示误差 #生成随机数x和y,拟合样本关系y = 8 + 4*x fig = plt.figure(figsize=(10,4)) ax1 = fig.add_subplot(121) plt.scatter(x,y,s = 10) plt.title('样本散点图') model = LinearRegression() # 创建线性回归模型 model.fit(x[:,np.newaxis],y) # 给模型导入样本值,第一个参数为自变量,第二个参数为因变量,x[:,np.newaxis]表示给x在列上增加一个维度,不能直接使用x print('斜率为%f,截距为%f'%(model.coef_,model.intercept_)) # 斜率为4.004484,截距为8.447659 xtest = np.linspace(0,10,1000) ytest = model.predict(xtest[:,np.newaxis]) # 通过模型预测自变量对应的因变量 ax1 = fig.add_subplot(122) plt.scatter(x,y,s = 10) plt.plot(xtest,ytest,color = 'red') #拟合线性回归直线 plt.title('线性回归拟合图')
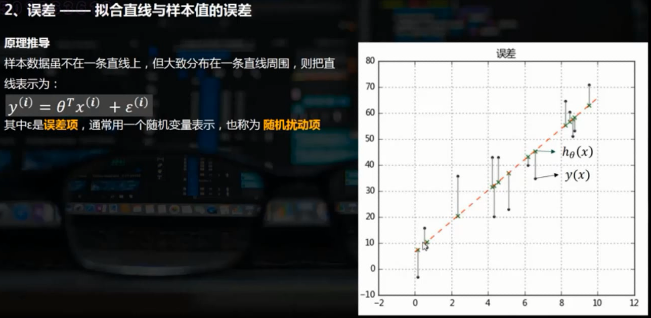
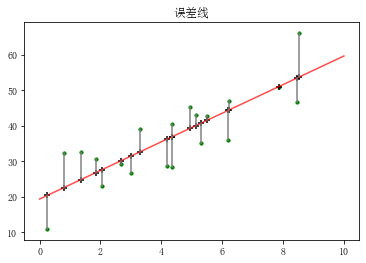
误差,即样本实际值与拟合得到的样本值的差
rng = np.random.RandomState(2) x = 10 * rng.rand(20) y = 8 + 4 * x + rng.rand(20)*30 #误差乘以20是为了在图表中明显显示 model = LinearRegression() model.fit(x[:,np.newaxis],y) xtest = np.linspace(0,10,1000) ytest = model.predict(xtest[:,np.newaxis]) plt.plot(xtest,ytest,color = 'r',alpha = 0.7) # 拟合线性回归直线 plt.scatter(x,y,s = 10,color='green') # 样本散点图 y2 = model.predict(x[:,np.newaxis]) # 样本x在拟合直线上的y值 plt.scatter(x,y2,marker = '+',color = 'k') # 样本x拟合y的散点图 plt.plot([x,x],[y,y2],color = 'gray') #误差线 plt.title('误差线')
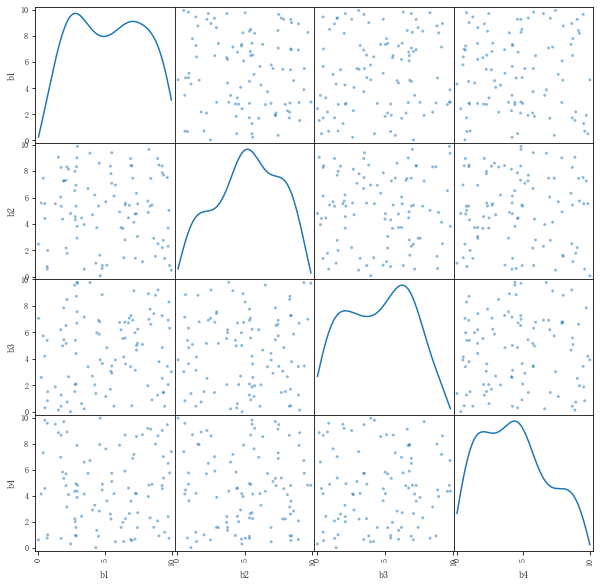
2.多元线性回归
矩阵点积参考https://blog.csdn.net/skywalker1996/article/details/82462499
rng = np.random.RandomState(3) x = 10 * rng.rand(100,4) y = 20 + np.dot(x,[1.5,2,-4,3]) + rng.rand(100) df = pd.DataFrame(x,columns=['b1','b2','b3','b4']) df['y'] = y df.head() pd.plotting.scatter_matrix(df[['b1','b2','b3','b4']],figsize = (10,10),diagonal='kde') #根据矩阵散点图判断4个变量之间相互独立,不需降维 model = LinearRegression() model.fit(df[['b1','b2','b3','b4']],df['y']) print('斜率为:',model.coef_,type(model.coef_)) print('截距为:',model.intercept_) print('线性回归函数为y = %.1fx1 + %.1fx2 + %.1fx3 + %.1fx4 + %.1f'%(model.coef_[0],model.coef_[1],model.coef_[2],model.coef_[3],model.intercept_)) # 斜率为: [ 1.50321961 2.0000257 -3.99067203 2.99358669] <class 'numpy.ndarray'> # 截距为: 20.489657423197222 # 线性回归函数为y = 1.5x1 + 2.0x2 + -4.0x3 + 3.0x4 + 20.5
四、线性回归模型评估
通过几个参数验证回归模型
- SSE:和方差、误差平方和,the sum of squares due to error
- MSE:均方差、方差,mean squared error
- RMSE:均方根、标准差,root mean squared error
- R-square:确定系数,coefficient of determination
1.SSE(和方差)
该统计参数计算的是拟合数据和原始数据对应点的误差的平方和,计算公式如下。
SSE越接近于0,说明模型选择和拟合更好,数据预测也越成功。接下来的MSE和RMSE因为和SSE同出一宗,效果一样。
2.MSE(均方差)
该统计参数是预测数据和原始数据对应点误差的平方和的均值,也就是SSE/n,和SSE没有太大的区别,计算公式如下。
3.RMSE(均方根)
该统计参数也叫回归系统的拟合标准差,是MSE的平方根,就算公式如下
在这之前,误差参数都是基于预测值和原始值之间的误差(即点对点),而下面的误差是相对原始数据平均值而展开的(即点对全)。
4.R-square(确定系数)
①SSR:Sum of squares of the regression,即预测数据与原始数据均值之差的平方和,公式如下。
②SST:Total sum of squares,即原始数据和均值之差的平方和,公式如下。
细心的网友会发现,SST=SSE+SSR,而“确定系数”是定义为SSR和SST的比值,故
其实“确定系数”是通过数据的变化来表征一个拟合的好坏。由上面的表达式可以知道“确定系数”的正常取值范围为[0,1],越接近1表明方程的变量对y的解释能力越强,这个模型对数据拟合的也较好。
from sklearn import metrics rng = np.random.RandomState(6) x = 10 * rng.rand(30) y = 8 + 4 * x + rng.rand(30) * 3 model = LinearRegression() model.fit(x[:,np.newaxis],y) # 回归拟合 ytest = model.predict(x[:,np.newaxis]) # 求出预测数据 sse = ((ytest - y)**2).sum() # 求SSE,也可通过该方法得到SSE,再除以len(x)得到MSE mse = metrics.mean_squared_error(ytest,y) # 求均方差MSE,也可通过该方法算出MSE,再乘以len(x)得到SSE rmse = np.sqrt(mse) # 求均方根RMSE # ssr = ((ytest - y.mean())**2).sum() # 求预测数据与原始数据均值之差的平方和 # sst = ((y - y.mean())**2).sum() # 求原始数据和原始数据均值之差的平方和 # rr = ssr / sst # 求确定系数 r = model.score(x[:,np.newaxis],y) # 求出确定系数 print('和方差SSE为:%.5f'%sse) print('均方差MSE为: %.5f'% mse) print('均方根RMSE为: %.5f'% rmse) print('确定系数R-square为: %.5f'% r) # 和方差SSE为:16.54050 # 均方差MSE为: 0.55135 # 均方根RMSE为: 0.74253 # 确定系数R-square为: 0.99512
5.线性回归模型评估总结
主要是用MSE和 R_square。
如果是对一个样本做两个回归模型,可以分别判断哪个MSE更小哪个就更好、哪个R接近于1哪个就更好。如果只有一个回归模型,判断R是否接近1,大于0.6、0.8就非常不错了。同时在后续做组成成分分析,假如有10个参数,做一个回归模型后做一个R模型评估,比如说R为0.85,把这10个参数降维为3个主成分,再做一个3元的线性回归,R为0.92,则3元线性回归模型的R为0.92更好,相互比较做出最优比较。
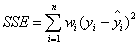
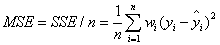
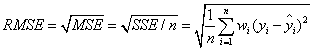
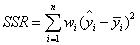
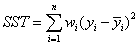
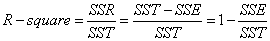

 浙公网安备 33010602011771号
浙公网安备 33010602011771号