数据标准化和离散化

在某些比较和评价的指标处理中经常需要去除数据的单位限制，将其转化为无量纲的纯数值，便于不同单位或量级的指标能够进行比较和加权。因此需要通过一定的方法进行数据标准化，将数据按比例缩放，使之落入一个小的特定区间。

一、标准化

1.0-1标准化

方法：将样本中的最大值、最小值记录下来，并通过max-min作为基数(即标准化后min=0、max=1)进行数据的归一化处理。

x = (x - min)/(max-min)

df = pd.DataFrame({'value1':np.random.rand(10)*10,'value2':np.random.rand(10)*100})
def f(data,*cols):
    df_n = data.copy()
    for col in cols:
        ma = df_n[col].max()  #每一列的最大值
        mi = df_n[col].min()  #每一列的最小值
        df_n[col+'_n'] = (df_n[col]-mi)/(ma -mi)  #计算各个样本标准化之后的值
    return df_n

df_n = f(df,'value1','value2')
df_n

2.Z-score标准化

z-score是一个数与样本平均数的差再除以标准差的过程 → z=(x-μ)/σ，其中x为某一具体数，μ为平均数，σ为标准差，Z值的量代表着原始数与母体平均值之间的距离，是以标准差为单位计算的。在原始数低于平均值时Z为负数，反之则为正数。数学意义：一个给定的数距离平均数多少个标准差。

在分类、聚类算法中，需要使用距离来度量相似性的时候，Z-score表现更好。

df = pd.DataFrame({'value1':np.random.rand(10)*100,'value2':np.random.rand(10)*100})
def f(data,*cols):
    df_n = data.copy()
    for col in cols:
        u = df_n[col].mean()
        std = df_n[col].std()
        df_n[col+'_n'] = (df_n[col] - u)/std
    return df_n

df_n = f(df,'value1','value2')
print(df_n)
u_n1 = df_n['value1_n'].mean()
std_n1 = df_n['value1_n'].std()
u_n2 = df_n['value2_n'].mean()
std_n2 = df_n['value2_n'].std()
print('标准化后value1的均值为%3.f，标准差为%.3f'%(u_n1,std_n1))
print('标准化后value2的均值为%3.f，标准差为%.3f'%(u_n2,std_n2))

案例应用

# 八类产品的两个指标value1，value2，其中value1权重为0.6，value2权重为0.4
# 通过0-1标准化，判断哪个产品综合指标状况最好
df = pd.DataFrame({"value1":np.random.rand(10) * 30,
                  'value2':np.random.rand(10) * 100},
                 index = list('ABCDEFGHIJ'))
#print(df.head())
#print('------')
# 创建数据"

def data_norm(data,*cols):
    df_n = data.copy()
    for col in cols:
        ma = df_n[col].max()  #每一列的最大值
        mi = df_n[col].min()  #每一列的最小值
        df_n[col+'_n'] = (df_n[col]-mi)/(ma -mi)  #计算各个样本标准化之后的值
    return df_n

df_n1 = data_norm(df,'value1','value2')
# 进行标准化处理

df_n1['f'] = df_n1['value1_n'] * 0.6 + df_n1['value2_n'] * 0.4
df_n1.sort_values(by = 'f',inplace=True,ascending=False)
df_n1['f'].plot(kind = 'line', style = '--.k', alpha = 0.8, grid = True)
df_n1.head()

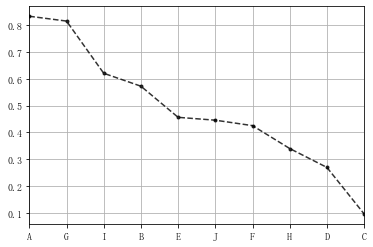
三、连续属性离散化

连续属性变换成分类属性，即连续属性离散化。

在数值的取值范围内设定若干个离散划分点，将取值范围划分为一些离散化的区间，最后用不同的符号或整数值代表每个子区间中的数据值

1.等宽法cut()

ages=[20,22,25,27,21,23,37,31,61,45,41,32]
bins = [18,25,35,60,100]   #按照18-25、25-35、35-60、60-100分为4个区间
age_cut = pd.cut(ages,bins)
print('分组结果：',age_cut,type(age_cut))  #分组后结果，显示每个值对应的区间
print('分组结果(代号表示)：',age_cut.codes, type(age_cut.codes))  # 显示每个值对应的区间代号，结果为ndarray；可以查看里边的等级
print('分组区间：',age_cut.categories, type(age_cut.categories))  # 四个区间，结果为IntervalIndex
print('分组统计:\n',pd.value_counts(age_cut))  # 按照分组区间计数
print('-------')

# 默认为左开右闭区间，right参数设置为False表示左闭右开区间
print(pd.cut(ages,[18,26,36,61,100],right=False)) 
print('-------')

# 通过labels参数自定义区间名称
group_names=['Youth','YoungAdult','MiddleAged','Senior']
print(pd.cut(ages,bins,labels=group_names))

# 分组结果： [(18, 25], (18, 25], (18, 25], (25, 35], (18, 25], ..., (25, 35], (60, 100], (35, 60], (35, 60], (25, 35]]
# Length: 12
# Categories (4, interval[int64]): [(18, 25] < (25, 35] < (35, 60] < (60, 100]] <class 'pandas.core.arrays.categorical.Categorical'>
# 分组结果(代号表示)： [0 0 0 1 0 0 2 1 3 2 2 1] <class 'numpy.ndarray'>
# 分组区间： IntervalIndex([(18, 25], (25, 35], (35, 60], (60, 100]],
#               closed='right',
#               dtype='interval[int64]') <class 'pandas.core.indexes.interval.IntervalIndex'>
# 分组统计:
#  (18, 25]     5
# (35, 60]     3
# (25, 35]     3
# (60, 100]    1
# dtype: int64
# -------
# [[18, 26), [18, 26), [18, 26), [26, 36), [18, 26), ..., [26, 36), [61, 100), [36, 61), [36, 61), [26, 36)]
# Length: 12
# Categories (4, interval[int64]): [[18, 26) < [26, 36) < [36, 61) < [61, 100)]
# -------
# [Youth, Youth, Youth, YoungAdult, Youth, ..., YoungAdult, Senior, MiddleAged, MiddleAged, YoungAdult]
# Length: 12
# Categories (4, object): [Youth < YoungAdult < MiddleAged < Senior]

输出结果

案例(使用上述例子中的ages、group_names和age_cut.codes)

df = pd.DataFrame({'ages':ages})
s = pd.cut(df['ages'],bins)  # 也可以 pd.cut(df['ages'],5),将数据等分为5份
df['label'] = s
cut_counts = s.value_counts(sort=False) 
# print(df)
# print(cut_counts)

plt.scatter(df.index,df['ages'],c = age_cut.codes)  #颜色按照codes分类
plt.grid()

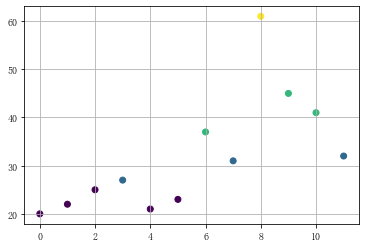
2.等频法qcut()

等频法是将样本数据按照个数平均进行分组

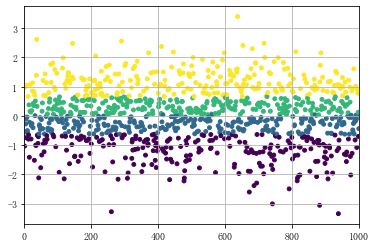
data = np.random.randn(1000)
s = pd.Series(data)
cats = pd.qcut(s,4)  # 按四分位数进行切割，可以试试 pd.qcut(data,10)
print(cats.head())
print(cats.value_counts())# qcut → 根据样本分位数对数据进行面元划分，得到大小基本相等的面元，但并不能保证每个面元含有相同数据个数
# 也可以设置自定义的分位数（0到1之间的数值，包含端点） → pd.qcut(data1,[0,0.1,0.5,0.9,1])

plt.scatter(s.index,s,s = 15 ,c = pd.qcut(data,4).codes)  #用散点图表示，其中颜色按照codes分类
plt.xlim([0,1000])
plt.grid()
# 注意codes是来自于Categorical对象

# 0    (-0.627, 0.0381]
# 1    (-3.348, -0.627]
# 2      (0.663, 3.403]
# 3    (-3.348, -0.627]
# 4    (-0.627, 0.0381]
# dtype: category
# Categories (4, interval[float64]): [(-3.348, -0.627] < (-0.627, 0.0381] < (0.0381, 0.663] < (0.663, 3.403]]
# (0.663, 3.403]      250
# (0.0381, 0.663]     250
# (-0.627, 0.0381]    250
# (-3.348, -0.627]    250
# dtype: int64