网络流学习笔记
我承认了,我粘的 LiveDream Classin里的图!
我没学费用流!
一·网络最大流
1.
这个只是铺垫(
https://oi-wiki.org/graph/flow/max-flow/

2.
当多条增广路有很长一部分的公共路径时,
如何使一条路只搜一次?
将经过节点
实现:
- 利用BFS将有向图分层,达到每次走最短路的目的
- 利用DFS的回溯特点,将一个点
我的
#include<bits/stdc++.h>
#define int long long
using namespace std;
int n,m,s,t,head[200005],nxt[200005],edge[200005],to[200005],pre[100005],level[100005];
int tot;
void add(int u,int v,int w){
to[++tot]=v;
edge[tot]=w;
nxt[tot]=head[u];
head[u]=tot;
to[++tot]=u;
edge[tot]=0;
nxt[tot]=head[v];
head[v]=tot;
}
bool bfs(){
memset(level,0,sizeof(level));
queue<int>q;
level[s]=1;
q.push(s);
while(!q.empty()){
int cur=q.front();
q.pop();
for(int i=head[cur];i;i=nxt[i]){
if(edge[i]&&!level[to[i]]){
q.push(to[i]);
level[to[i]]=level[cur]+1;
if(to[i]==t)return 1;
}
}
}
return 0;
}
int Dinic(int x,int flow){
if(x==t)return flow;
int rest=flow,increase;
for(int i=head[x];i&&rest;i=nxt[i]){
int y=to[i];
if(edge[i]&&level[y]==level[x]+1){
increase=Dinic(y,min(rest,edge[i]));
if(!increase)level[y]=0;
edge[i]-=increase;
edge[i^1]+=increase;
rest-=increase;
}
}
return flow-rest;
}
signed main(){
ios::sync_with_stdio(0);
cin>>n>>m>>s>>t;
cin.tie(0);
cout.tie(0);
tot=1;
for(int i=1;i<=m;++i){
int u,v,w;
cin>>u>>v>>w;
add(u,v,w);
}
int flow=0,maxflow=0;
while(bfs())maxflow+=Dinic(s,1000000000);
cout<<maxflow;
return 0;
}
最大流中的最小割问题:
使得原点
结论:最小割=最大流(割的和上限边是同一个边)
最大权闭合子图问题
什么是闭合子图?
在有向图G(V,E)中,存在子图G'(V',E'),使得V'中的点
沿着E'到达的顶点x也是V'中的点,那么G'就是G的闭合子图。
什么是最大权闭合子图?
权值在点上,所有闭合子图中,点权和最大的闭合子图
问题雏形
给定 n 种物品,均有价格,m 个组合对应 m 种收益(可重叠,价格只算一次,收益重叠),求最大收益。
建模方法


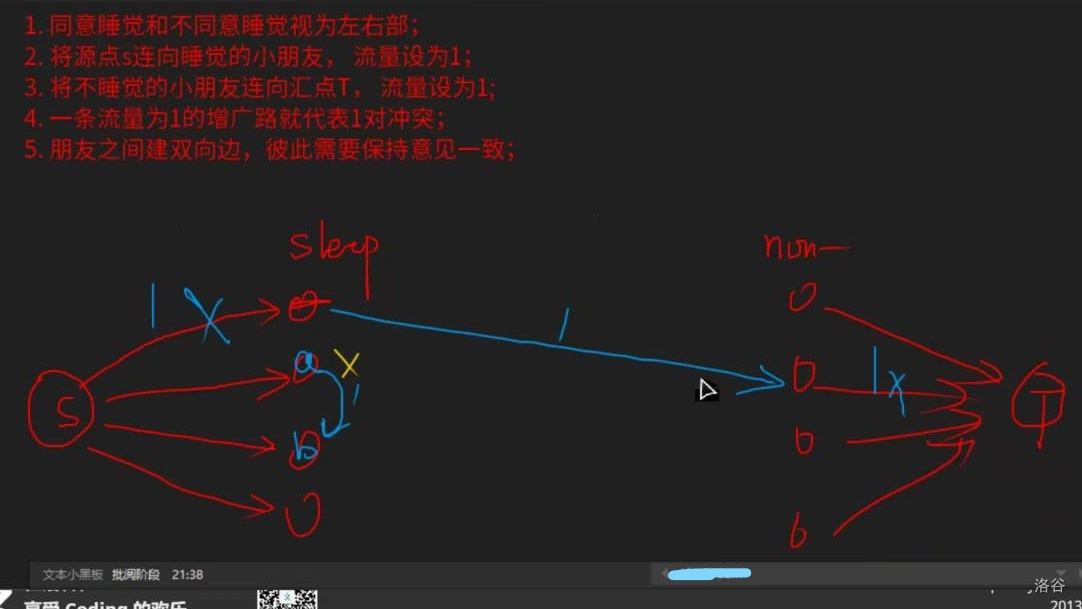


【推荐】国内首个AI IDE,深度理解中文开发场景,立即下载体验Trae
【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步
· 分享一个免费、快速、无限量使用的满血 DeepSeek R1 模型,支持深度思考和联网搜索!
· 基于 Docker 搭建 FRP 内网穿透开源项目(很简单哒)
· 25岁的心里话
· ollama系列01:轻松3步本地部署deepseek,普通电脑可用
· 按钮权限的设计及实现