SAM学习笔记&AC自动机复习
形势所迫,一个对字符串深恶痛绝的鸽子又来更新了。
SAM
后缀自动机就是一个对于字符串所有后缀所建立起的自动机。一些优良的性质可以使其完成很多字符串的问题。
其核心主要在于每个节点的状态和$endpos$这个概念的结合:“状态”定义为从源点出发到达当前节点的所有字符串,$endpos$对于一个字符串它作为整个字符串子串的结尾位置的集合,而SAM则保证状态和相同的$endpos$集合构成一个一一映射。
容易证明在同一个状态的字符串互为后缀,记最长的那个为$longest(x)$,但是不保证所有同后缀的字符串都是同一个状态,所以我们从一个状态连到前面的一个状态,记连边为$link$,表示被连的那个状态$endpos$比当前这个多。这样的边构成的DAG称之为$parent tree$,容易发现,被连状态的$longest(x)$为连向它的状态的$longest(x)$的后缀。
接下来考虑如何建立SAM,考虑一个一个加进字符,在$X$后加入$S$,我们分三类讨论:
1.记在$parent tree$跳到的节点为$p$,如果$p$没有向$S$连的边,那么直接连边即可。
2.$p$有向$S$连的边,而且$longest(p)+1=longest(p+S)$,那么就说明第一个$p+S$是对于新加入节点第一个$endpos$产生分裂的地方,那么$link[X+S]=p+S$
3.最烦的情况:即连出去的那条边是“飞出去的”
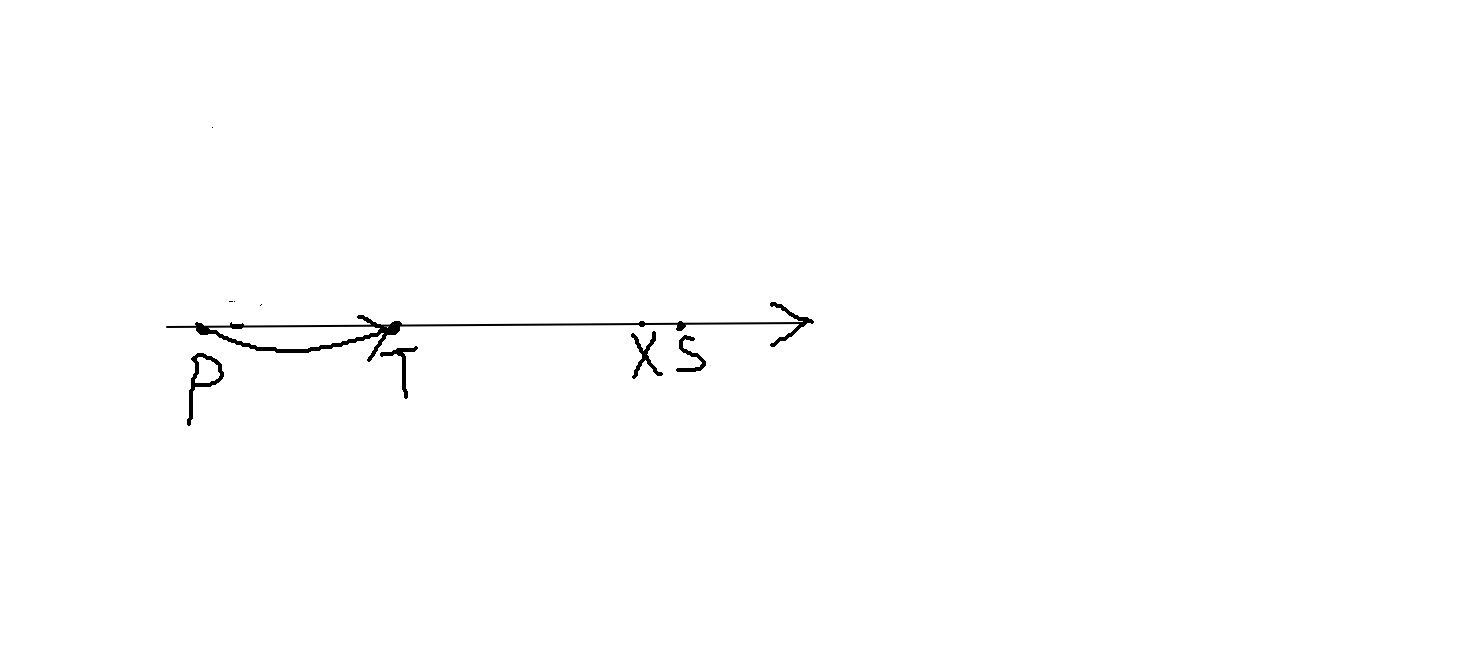
考虑从这个性质,因为从X连到P,所以从起点连到P的$longest$一定是X的后缀,而P的转移边是到T,所以$longest(P+S)$必然在$T$中作为一个后缀。
所以在加上S以后T中的一个后缀(不是T且现在无法表示出,但是必然在字符串中)和X+S不再属于同一个$endpos$,这是第一个断点(即T状态下以字符$S$结尾的不再属于这个状态,或者说无法再根据该自动机的前缀表示所有子串)。所以要从中间截取出一个作为新的状态,$longest$长度应当是$longest(P)+1$。(这个节点也是T的第一个断点)
即:
拆分出$y$,使得$trans[p...w]=y$($w$是最后一个$trans[w]=T$),然后$y$继承$T$,$link[y]=link[T]$,$link[T]=link[X+S]=y$
代码:
struct SAM{ int link[N],maxlen[N],trans[N][26],f[N]; void extend(int id){ int cur=++sz,p; f[sz]=1; maxlen[cur]=maxlen[lst]+1; for(p=lst;p&&!trans[p][id];p=link[p]) trans[p][id]=cur; if(!p) link[cur]=1; else{ int q=trans[p][id]; if(maxlen[q]==maxlen[p]+1) link[cur]=q; else{ int tmp=++sz; maxlen[tmp]=maxlen[p]+1; copy(trans[q],trans[q]+26,trans[tmp]); link[tmp]=link[q]; for(;p&&trans[p][id]==q;p=link[p]) trans[p][id]=tmp; link[cur]=link[q]=tmp; } } lst=cur; } }tree;
目前只会板子这种,联赛以后再填坑。
时间坐标12.14,时隔一个半月我来更新啦~\(≧▽≦)/~
统计单个子串出现个数
考虑SAM构建出来的$parenttree$就是一棵虚树,其中儿子的后缀集合包含父亲的后缀集合(父亲就是儿子的后缀集合分出来的较短的一部分),所以直接儿子转移到父亲,在$maxlen$处统计即可,注意虚点不能有贡献。
本质不同子串个数
有两种方法,一种是直接利用$trans$在DAWG上dp,$dp[i]$表示以$i$为后缀的本质不同方案数,SAM的性质保证一个点不会由被相同状态更新。
还有一种方法是利用$endpos$,它对于每一个状态的$endpos$集合都是唯一的,所以重复出现的只会出现一次(最前面),然后直接统计其独有的集合大小即可。
集合大小为一个状态(互为后缀)的$maxlen-minlen+1=maxlen-maxlen[link]$,到这一步其实也可以用容斥的方法来理解(后缀集合较大的减去第一个包含的,就是独有的)。
SA的做法其实也是容斥,答案为$\sum n-sa[i]+1-height[i]$
因此SAM上所有状态不交地并成了子串全集(所以检验匹配串是否存在直接从起点开始跳就好了,“状态”其实是在所有后缀中找一个前缀)。
补充一下,对于“不同子串总长度”也可以用两种方法,后者等差数列即可,对于前者,我们可以拆贡献,把一个状态辐射出去的多个子串的一位一起统计。
即:令$dp[i]$表示以状态$i$开始的不同路径数量,那么$ans[u]=dp[u]+ \sum ans[to]$
第K大子串
如果是要求子串本质不同,那么直接利用dp搞出来每一个状态不同后缀个数,然后直接类似线段树上二分一样搞一搞就好了。
如果没有要求本质不同,前面状态的各个子串其实是后面的真子集,但是要保证到达这位的时候把后面所有相同的串统计进去,那么就要把后面的状态通过$link$进行一个dp,使得原先去掉重的再通过$link$还原回来。
任意两点LCP
除了SA之外,SAM也可以实现类似的功能。
把字符串反过来插到SAM里面,然后两点在$parenttree$上的LCA的$longest$就是所求。(大概可以用“任意状态和子串一一映射”“link所连互为后缀”来理解)
(中间新加的非字符串的点可以认为是虚点。建出来的东西大概就相当于在SA的$height$数组上建笛卡尔树)
第一次出现位置
在建立SAM的时候直接转移就可以了,每个状态的$endpos$是相同的,所以维护一个$firstpos$。对于加入字符的节点,$firstpos=maxlen$,如果是复制的点那么$firstpos=firstpos[q]$,因为$link$它的只有两个——$cur$和$q$(前面状态的$endpos$包含后面的,后面的后缀集合包含前面的),显然$q$更小。
两个串的最长公共子串
其实$parenttree$原理和AC自动机的$fali$树差不多(SAM是多个串来匹配一个串,AC自动机是一个串去扫所有串),对于S建立SAM,然后T上来暴力匹配,如果匹配了就当前长度+1;如果失配,那么直接把长度赋值成$link$的$maklen$即可。
(可能是我之前理解有些偏差,对于一个实的状态,对于以它$r$结尾的所有后缀,只有左端点$[1,l]$的是属于它的,$[l+1,r]$则分别分配在$parenttree$的父亲上,所以$link$所连向的最大字符串是该状态所有字符串的子串,它是最大的在另外位置出现的子串。)
最短未出现子串
考虑上一个匹配的时候的算法:如果从一个点出发只要有一个字符连不出去,那么在这个节点后加上这个字符就肯定不是了,所以令$dp[x]=1$,然后往前dp即可
区间本质不同子串
小编也不想做这么重工业的题,但模拟赛出了。。
首先先要解锁一下LCT的新用法:打通一个点到根的所有路径,顺便把这条路径上要改的点全改了(可以是虚边,也可以是全部)。
那么在SAM的$parenttree$上一个点到根意味着什么?——状态代表的子串并就是它后缀集合集合里面的所有元素。
然后看这个问题。考虑一个经典问题——求区间不同颜色数,那么我们可以把询问离线扫右端点,尽量使得每种颜色的贡献尽量靠右,然后树状数组统计即可。
这里也可以考虑使得本质相同的子串尽量靠右。
那么就是上文所说的,在新加入一个右端点的时候,把它后缀集合里所有元素,即长度为$[1,r]$的所有子串全部更新最右的左端点,修改在一个线段树上,然后线段树直接查询左端点即可。
(突然想起来,要把所有后缀集合并在一起,就是一个点到根的所有值并(就是$maxlen$);那么如果是把$endpos$并起来,就是从底下开始(叶子肯定只有一个元素),然后线段树合并就行了)


