Educational Codeforces Round 113 (Rated for Div. 2) 题解
旅行传送门
一些闲话:打得稀碎,不知道为什么昨晚状态差的一逼,20分钟应该切出来的题硬生生看了两小时,难受到一宿都没睡好,做梦都在想题,所幸今天早上起来状态好点了,补题的时候不至于像昨晚那样没思路了,虽然掉大分还是很心痛(っ╥╯﹏╰╥c)
A. Balanced Substring
题意:给你一个仅由字母 \(a\) 、 \(b\) 组成的字符串 \(s\) ,要你找到某个区间,使得区间内字母 \(a\) 、 \(b\) 的个数相等。
题目分析:签到题切了20分钟,一开始还准备拿双指针去瞎搞,我都不知道自己在想些啥。
考虑最简单的情况,只需要找是否存在子串 \(ab\) 或 \(ba\) 就好了,如果没有,那么这样的区间可以证明一定不存在。
AC代码:
//代码早上起来重修的,昨晚写的不知道是什么sh*t
#include <bits/stdc++.h>
#define rep(i, x, y) for (register int i = (x); i <= (y); i++)
#define down(i, x, y) for (register int i = (x); i >= (y); i--)
#define pii pair<int, int>
#define mp make_pair
using namespace std;
pii solve()
{
int n;
cin >> n;
string s;
cin >> s;
pii res = mp(-1, -1);
string m1 = "ab", m2 = "ba";
int pos = s.find(m1);
if (pos != s.npos)
{
res.first = pos + 1, res.second = pos + 2;
return res;
}
pos = s.find(m2);
if (pos != s.npos)
{
res.first = pos + 1, res.second = pos + 2;
return res;
}
return res;
}
int main(int argc, char const *argv[])
{
ios::sync_with_stdio(false);
cin.tie(nullptr);
int t;
cin >> t;
while (t--)
{
pii ans = solve();
printf("%d %d\n", ans.first, ans.second);
}
return 0;
}
B. Chess Tournament
题意: \(n\) 位选手参加比赛。两两battle一场。 每场比赛的结果要么是一方胜一方负,要么是双方平局。
每位选手都有自己的期望,他们是以下两者之一:
- 选手不希望输掉任何一场比赛
- 选手想要至少赢得一场比赛
问是否可以满足所有选手的期望,若可以则输出比赛结果。
题目分析:我是傻逼,简简单单的签到题硬是先写加了一大堆if else的sh*t mountain代码wa了整整两发,之后又写了份晦涩难懂的代码a了,被自己整无语了(流汗黄豆)。
先考虑什么情况下不能满足,若拥有第二种期望(不爆零)的选手数量为 \(1\) 或 \(2\) ,则输出 \(NO\) 。很好理解,在此不过多赘述。
之后扫一遍整个字符串,假设第 \(i\) 位选手期望为 \(1\) ,就把第 \(i\) 行 \(i\) 列都划上等号(视为平局),否则就在当前行第一个空位赢一把,之后的都输掉就行了。
AC代码:
#include <bits/stdc++.h>
#define rep(i, x, y) for (register int i = (x); i <= (y); i++)
#define down(i, x, y) for (register int i = (x); i >= (y); i--)
const int maxn = 55;
char s[maxn];
int mp[maxn][maxn];
int main(int argc, char const *argv[])
{
int t;
scanf("%d", &t);
while (t--)
{
memset(mp, 0, sizeof(mp));
int n;
scanf("%d", &n);
scanf("%s", s + 1);
int n1 = 0, n2 = 0;
rep(i, 1, n) s[i] == '1' ? ++n1 : ++n2;
if (n1 == n)
{
puts("YES");
rep(i, 1, n)
{
rep(j, 1, n) i == j ? printf("X") : printf("=");
puts("");
}
continue;
}
if (n2 == 1 || n2 == 2)
{
puts("NO");
continue;
}
rep(i, 1, n) if (s[i] == '1') rep(j, 1, n) mp[i][j] = mp[j][i] = 3;
rep(i, 1, n) rep(j, 1, n) if (i == j) mp[i][j] = 4;
rep(i, 1, n)
{
if (s[i] == '2')
{
int flag = 0;
rep(j, 1, n)
{
if (flag)
mp[i][j] = 2, mp[j][i] = 1;
if (!mp[i][j])
mp[i][j] = 1, mp[j][i] = 2, flag = 1;
}
}
}
puts("YES");
rep(i, 1, n)
{
rep(j, 1, n)
{
if (mp[i][j] == 1)
printf("+");
else if (mp[i][j] == 2)
printf("-");
else if (mp[i][j] == 3)
printf("=");
else if (mp[i][j] == 4)
printf("X");
}
puts("");
}
}
return 0;
}
C. Jury Meeting
题意: 给你一个序列 \(a\) ,让你确定一个顺序,按这个顺序依次递减(已经为 \(0\) 的元素则跳过)直至序列元素全为 \(0\) 为止,递减过程中,若没有一个元素连续减两次,则称其为“好顺序”,问共有多少个好顺序?
举栗子:
假设序列 \(a\) 中包含元素 \(1、2、3\) 。
按\(1、3、2\) 排序: \([1,3,2]\) -> \([0,2,1]\) -> \([0,1,0]\) -> \([0,0,0]\) 好顺序
按\(1、2、3\) 排序: \([1,2,3]\) -> \([0,1,2]\) -> \([0,0,1]\) -> \([0,0,0]\) 坏顺序( \(a_3\) 被不间断地连续减了两次)
题目分析:先分三种情况讨论吧:
- 记最大值为 \(max\) ,若 \(max\) 的个数 \(\geq 2\) ,显然不管按什么顺序递减都是好顺序,此时 \(ans\) 为 \(A_{n}^{n}\)
- 记最大值为 \(max\) ,次大值为 \(cmax\) ,若两者差值 \(\geq 2\) ,显然不管按什么顺序递减都是坏顺序,因为其它值都减为 \(0\) 的时候最大值所余留的值必定 \(\geq 2\) ,必定会被不间断地连续减两次,此时 \(ans\) 为 \(0\)
- 排除以上两种情况后,设元素个数为 \(n\) ,其它值(除最大值和次大值以外的值)的个数为 \(t\) ,最初 \(ans\) 为总排列 \(A_{n}^{n}\) ,最大值处于序列末尾时,无论前面怎么排都是坏顺序, \(ans\) 先减去 \(A_{n-1}^{n-1}\)
- 之后最大值从末尾依次向前推进,后面随之留出空位,我们记空位数为 \(m\) ,那么 \(m\) 循环从 [\(1\) -> \(t\)] ,\(ans\) 每次减去 \(C_{t}^{m} \times m! \times (n-m-1)!\) ,最终结果即为所求, \(C_{t}^{m}\) 是从 \(t\) 个其它值中选出 \(m\) 个填入空位,最大值前后的排序方案数分别为 \(m!\) 与 \((n-m-1)!\) 。
- 还是举个栗子说人话,比如序列包含元素 \(1、2、3、4、5\) ,一开始 \(ans = 120\) ,减去 \(5\) 在末尾的方案数后 \(ans = 96\) ,然后 \(5\) 向前推进一位,有 [ _ , _ , _ , \(5\) , _ ] ,次大值 \(4\) 必须放在 \(5\) 前面(这时才能构成坏顺序),那么 \(ans\) 就要再减去 \(C_{3}^{1} \times 1! \times A_{3}^{3}\) ,这样做下去最终 \(ans\) 为 \(60\) 。
AC代码:
#include <bits/stdc++.h>
#define rep(i, x, y) for (register int i = (x); i <= (y); i++)
#define down(i, x, y) for (register int i = (x); i >= (y); i--)
using ll = long long;
const int mod = 998244353;
const int maxn = 2e5 + 5;
char buf[1 << 23], *p1 = buf, *p2 = buf, obuf[1 << 23], *O = obuf;
#define getchar() (p1 == p2 && (p2 = (p1 = buf) + fread(buf, 1, 1 << 21, stdin), p1 == p2) ? EOF : *p1++)
inline ll read()
{
ll x = 0, f = 1;
char ch = getchar();
while (!isdigit(ch))
{
if (ch == '-')
f = -1;
ch = getchar();
}
while (isdigit(ch))
{
x = x * 10 + ch - '0';
ch = getchar();
}
return x * f;
}
ll t, fac[maxn], inv[maxn], a[maxn];
ll cal(ll t, ll m)
{
ll res = 1;
rep(i, 1, m) res = (res % mod * (t - m + i) % mod) % mod;
return res;
}
ll fpow_mod(ll a, ll b)
{
ll ans = 1;
while (b)
{
if (b & 1)
ans = ans * a % mod;
a = a * a % mod;
b >>= 1;
}
return ans;
}
ll getC(ll n, ll m) //C(n,m) = n!/((n-m)!*m!) % mod
{
return fac[n] * inv[n - m] % mod * inv[m] % mod;
}
ll solve()
{
ll n = read();
fac[0] = inv[0] = 1;
rep(i, 1, n)
{
fac[i] = 1ll * fac[i - 1] * i % mod;
inv[i] = fpow_mod(fac[i], mod - 2);
}
ll mx = 0, cnt = 0;
rep(i, 1, n)
{
a[i] = read();
if (a[i] > mx)
mx = a[i], cnt = 1;
else if (a[i] == mx)
++cnt;
}
if (cnt > 1)
return fac[n];
std::sort(a + 1, a + n + 1);
cnt = 0;
if (a[n] - a[n - 1] > 1)
return 0;
rep(i, 1, n) if (a[i] == a[n - 1])++ cnt;
ll others = n - cnt - 1;
ll res = fac[n];
res = (res - fac[n - 1] + mod) % mod;
rep(i, 1, others)
{
res = (res - ((getC(others, i) * fac[i]) % mod * fac[n - i - 1]) % mod + mod) % mod;
}
return res;
}
int main(int argc, char const *argv[])
{
t = read();
while (t--)
printf("%lld\n", solve() % mod);
return 0;
}
你以为就这样结束了?
没有
其实有更简单的做法
早上和大哥聊起这个题时,大哥听了我的思路,很是疑惑不解:为什么不直接算答案?
假设次大值个数为 \(k\) ,最大值和次大值一共有 \(k+1\) 种位置关系,而只有一种关系不合法,所以答案就是 \(n! \times \frac{k}{k+1}\) 。
嗯,我果然傻逼。
AC代码:
#include <bits/stdc++.h>
#define rep(i, x, y) for (register int i = (x); i <= (y); i++)
#define down(i, x, y) for (register int i = (x); i >= (y); i--)
using ll = long long;
const int mod = 998244353;
const int maxn = 2e5 + 5;
char buf[1 << 23], *p1 = buf, *p2 = buf, obuf[1 << 23], *O = obuf;
#define getchar() (p1 == p2 && (p2 = (p1 = buf) + fread(buf, 1, 1 << 21, stdin), p1 == p2) ? EOF : *p1++)
inline ll read()
{
ll x = 0, f = 1;
char ch = getchar();
while (!isdigit(ch))
{
if (ch == '-')
f = -1;
ch = getchar();
}
while (isdigit(ch))
{
x = x * 10 + ch - '0';
ch = getchar();
}
return x * f;
}
ll t, fac[maxn], inv[maxn], a[maxn];
ll cal(ll t, ll m)
{
ll res = 1;
rep(i, 1, m) res = (res % mod * (t - m + i) % mod) % mod;
return res;
}
ll fpow_mod(ll a, ll b)
{
ll ans = 1;
while (b)
{
if (b & 1)
ans = ans * a % mod;
a = a * a % mod;
b >>= 1;
}
return ans;
}
ll divi(ll a, ll b)
{
b = fpow_mod(b, mod - 2); //b的逆元
return a * b % mod;
}
ll solve()
{
ll n = read();
fac[0] = inv[0] = 1;
rep(i, 1, n)
{
fac[i] = 1ll * fac[i - 1] * i % mod;
inv[i] = fpow_mod(fac[i], mod - 2);
}
ll mx = 0, cnt = 0;
rep(i, 1, n)
{
a[i] = read();
if (a[i] > mx)
mx = a[i], cnt = 1;
else if (a[i] == mx)
++cnt;
}
if (cnt > 1)
return fac[n];
std::sort(a + 1, a + n + 1);
cnt = 0;
if (a[n] - a[n - 1] > 1)
return 0;
rep(i, 1, n) if (a[i] == a[n - 1])++ cnt;
ll res = fac[n] * divi(cnt, cnt + 1) % mod;
return res;
}
int main(int argc, char const *argv[])
{
t = read();
while (t--)
printf("%lld\n", solve());
return 0;
}
D. Inconvenient Pairs
题意:在一个直角坐标系中,给你一些水平线和竖直线,还有一些在直线上的点,点只能在线上移动。问你有多少个点对满足它们之间的距离大于它们的曼哈顿距离?
题目分析:我们不妨将点分为三种类型:
- 只在水平线上
- 只在竖直线上
- 在水平线和竖直线的交汇处
显然第三种点到其它点的距离都等于曼哈顿距离,而对于前两种情况的点,不难发现在水平线上的点与竖直线上的点之间的距离也一定是曼哈顿距离,所以有贡献的点对只会出现在两个点都是情况一或情况二上,在此不给出证明了(因为我也证不出),画下图应该很好理解。
那什么条件下,在同一种类型的直线上的两点会对答案有贡献呢,通过观察可以发现,若两点间不存在另一种类型的直线,那一个点就必须得“绕远路”才能走到另一个点,这个时候的点对即为合法的!说人话就是,比如样例中的点 \(3\) 与点 \(4\) 点 \(5\) 就是,这三个点都在竖直线上,但它们之间都没有“夹着”一条水平线,因此任两点都能作出贡献,而点 \(5\) 与点 \(8\) 之间就夹了一条 \(y = 4\) 的水平直线,所以这两个点就没贡献。
那么我们的任务就转换成如何统计这些点对了,首先我们把这三种类型的点分出来,一开始我想的是用树状数组,在竖直线上点的插水平线的值统计,水平线上的插竖直线统计,但是时间复杂度还是太高了,后来看了看其它julao的题解,直接枚举直线,统计相邻两直线间夹的点,这里给个旅行传送门。
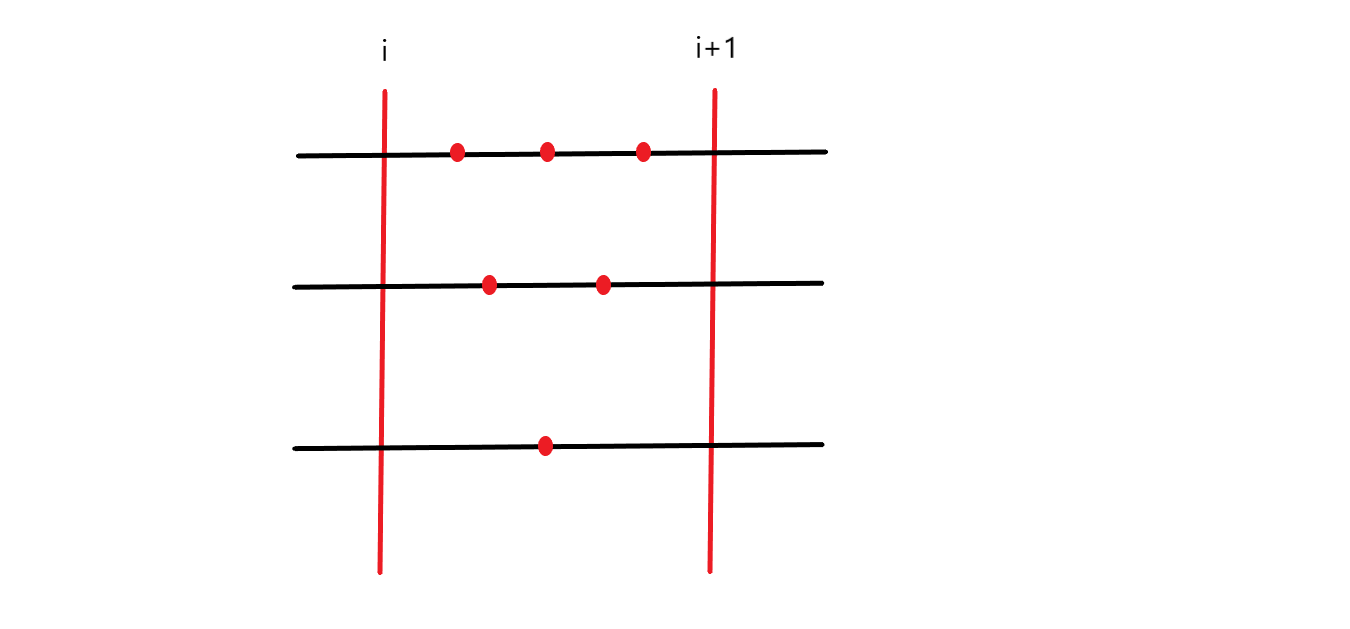
稍微解释下julao的博客,如图:
现在这两条直线间存在 \(6\) 个点,所以我们用 \(map\) 记录下每个点所在的直线坐标,这样就解决了多个点在同一直线的问题(因为在同一直线上的两点是不会有贡献的),那么这次更新的话新增的贡献即为:\(1 \times 5 + 2 \times 3\) 。
AC代码:
#include <bits/stdc++.h>
#define rep(i, x, y) for (register int i = (x); i <= (y); i++)
#define down(i, x, y) for (register int i = (x); i >= (y); i--)
#define pii std::pair<int, int>
using ll = long long;
const int maxn = 3e5 + 5;
char buf[1 << 23], *p1 = buf, *p2 = buf, obuf[1 << 23], *O = obuf;
#define getchar() (p1 == p2 && (p2 = (p1 = buf) + fread(buf, 1, 1 << 21, stdin), p1 == p2) ? EOF : *p1++)
inline int read()
{
int x = 0, f = 1;
char ch = getchar();
while (!isdigit(ch))
{
if (ch == '-')
f = -1;
ch = getchar();
}
while (isdigit(ch))
{
x = x * 10 + ch - '0';
ch = getchar();
}
return x * f;
}
std::vector<int> vs(maxn), hs(maxn), vx(maxn), vy(maxn);
std::vector<pii> ps(maxn);
inline bool cmp1(int a, int b) { return ps[a].second < ps[b].second; }
inline bool cmp2(int a, int b) { return ps[a].first < ps[b].first; }
ll solve()
{
ll res = 0;
int n = read(), m = read(), k = read();
std::map<int, int> mpx, mpy, mp;
rep(i, 1, n)
{
vs[i] = read();
++mpx[vs[i]];
}
rep(i, 1, m)
{
hs[i] = read();
++mpy[hs[i]];
}
int n1 = 0, n2 = 0;
rep(i, 1, k)
{
int x = read(), y = read();
ps[i] = std::make_pair(x, y);
if (mpx[x] && !mpy[y])
vx[++n1] = i;
if (!mpx[x] && mpy[y])
vy[++n2] = i;
}
std::sort(vx.begin() + 1, vx.begin() + n1 + 1, cmp1);
std::sort(vy.begin() + 1, vy.begin() + n2 + 1, cmp2);
int num = 1;
rep(i, 1, n - 1)
{
int point = 0;
while (num <= n2 && ps[vy[num]].first > vs[i] && ps[vy[num]].first < vs[i + 1])
{
++mp[ps[vy[num]].second];
++point;
++num;
}
for (auto it : mp)
{
point -= it.second;
res += 1ll * point * it.second;
}
mp.clear();
}
num = 1;
rep(i, 1, m - 1)
{
int point = 0;
while (num <= n1 && ps[vx[num]].second > hs[i] && ps[vx[num]].second < hs[i + 1])
{
++mp[ps[vx[num]].first];
++point;
++num;
}
for (auto it : mp)
{
point -= it.second;
res += 1ll * point * it.second;
}
mp.clear();
}
return res;
}
int main(int argc, char const *argv[])
{
int t = read();
while (t--)
printf("%lld\n", solve());
return 0;
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号