P2158 [SDOI2008]仪仗队 题解

旅行传送门：https://www.luogu.com.cn/problem/P2158

题目描述

作为体育委员，C君负责这次运动会仪仗队的训练。仪仗队是由学生组成的N * N的方阵，为了保证队伍在行进中整齐划一，C君会跟在仪仗队的左后方，根据其视线所及的学生人数来判断队伍是否整齐(如下图)。

现在，C君希望你告诉他队伍整齐时能看到的学生人数。

 

输入格式

共一个数N

输出格式

共一个数，即C君应看到的学生人数。

输入输出样例

输入 #1复制

4

输出 #1复制

9

 解题思路

以左下角C君所在的点为原点，第一行为x轴，第一列为y轴建立平面直角坐标系。不难发现，一条直线上只有第一个点能被看见，而直线的斜率 k = y / x，即点(x , y)能被看见的条件为其与原点的连线的斜率是第一次出现；我们又知道，分数化为最简形式时有：gcd (x , y) = 1,即x与y互质，那么我们的问题就转化为了求有几对互质的x与y。

在数论中，对正整数n，欧拉函数是小于或等于n的正整数中与n互质的数的数目(因此φ(1)=1)。因此，方阵下三角中互质的x与y的对数即为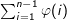(方阵为n * n的大小，而坐标轴的起点是由0开始计算，所以只累加至n - 1)，由于方阵关于y = x对称，最后输出答案2 *  + 1即可(y = x 上还有一点)。

欧拉函数

 

度娘与各大神犇对该函数的证明过程远远胜过本蒟蒻，在此就不过多赘述了。

AC代码

//打表版(3~6s)
#include <bits/stdc++.h>
#define MAXN 40000 + 10

int phi[MAXN],ans[MAXN];

void euler()
{
    ans[1] = 1;
    for (int i = 1; i <= MAXN; i++)
    {
        int res = i, n = i;
        for (int j = 2; j * j <= n; j++)
        {
            if (!(n % j))
                res = res * (j - 1) / j;
            while (!(n % j))
                n /= j;
        }
        if (n > 1)
            res = res * (n - 1) / n;
        phi[i] = res;
    }
    for (int i = 2; i <= MAXN; i++)
        for (int j = 1; j < i; j++)
            ans[i] += phi[j];
}

int main(int argc, char const *argv[])
{
    euler();
    int n;
    while (~scanf("%d", &n))
    {
        if (n == 1) //方阵大小为1*1时特判，此时队列中只有自己，输出0
        {
            puts("0");
            continue;
        }
        printf("%d\n", 2 * ans[n] + 1);
    }
    return 0;
}

//优化版(55±5ms)
#include <bits/stdc++.h>
#define MAXN 40000 + 10

int main(int argc, char const *argv[])
{
    int n, ans;
    while (~scanf("%d", &n))
    {
        ans = 0;
        if (n == 1)
        {
            printf("%d\n", 0);
            continue;
        }
        for (int i = 1; i < n; i++)
        {
            int res = i, t = i;
            for (int j = 2; j * j <= t; j++)
            {
                if (!(t % j))
                    res = res * (j - 1) / j;
                while (!(t % j))
                    t /= j;
            }
            if (t > 1)
                res = res * (t - 1) / t;
            ans += res;
        }
        printf("%d\n", 2 * ans + 1);
    }
    return 0;
}