【学习笔记】主席树详解——让你躺着学会主席树

学习笔记——主席树

前排感谢lfw学长，本文部分内容借鉴了学长撰写的ppt

很久很久以前，第k小问题突然出现……

有这样一棵线段树，它领悟了动态开点，经历了持久化，装备上了权值，最后得到了西主席的赐名，成功升级为了全新版本的线段树——主席树。
主席树的全称是可持久化权值线段树，即主席树⫋可持久化线段树。

首先，我们来回顾下线段树：

线段树是一种二叉搜索树，与区间树相似，它将一个区间划分成一些单元区间，每个单元区间对应线段树中的一个叶结点。
线段树支持单点与区间的修改与查询操作，复杂度均为logn级别。

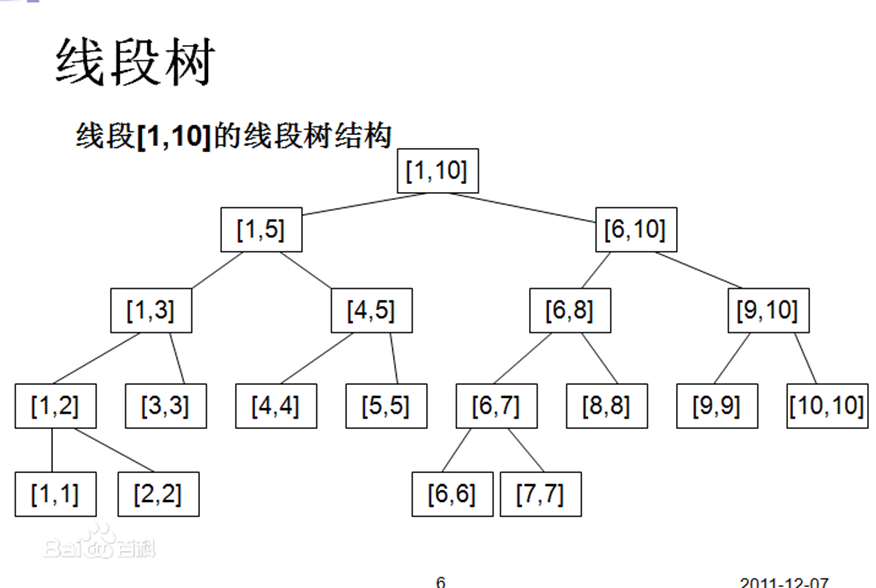
何为动态开点？

动态开点线段树是线段树的变种之一，与普通的线段树不同的是，它是白手起家，并没有建树的过程，而是哪里要用开哪里，每个节点的左右子树的编号不再是该点编号固定的2倍和2倍+1，而是根据当前所开的节点数确定。

引用其它blog的话，就是建立一棵“残疾”的线段树，上面只有询问过的相关节点。从而节约了大量空间，这样当你面对庞大的数据时，也能如鱼得水，游刃有余。

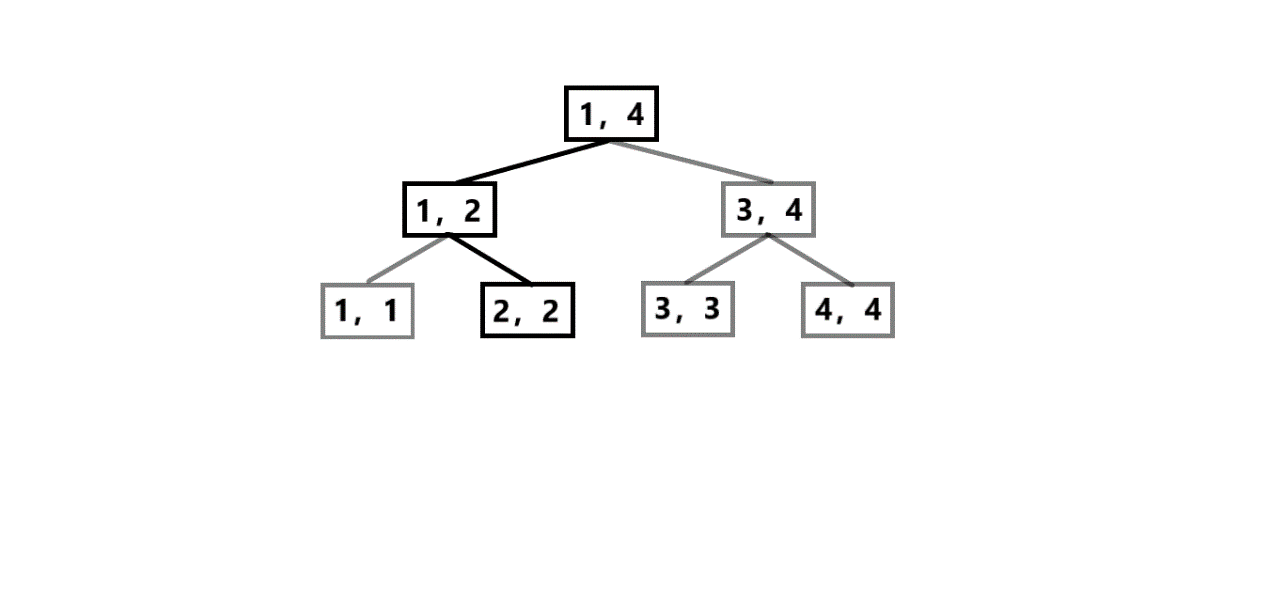
图中黑色水墨的点为之前进行了相关操作开了的点，浅墨的点为还没开的点（被加上了阿卡林力场）。

何为可持久化？

于数据结构而言，可持久化总是可以保留每一个历史版本，并且支持操作的不可变特性。
而可持久化线段树的本质就是多根线段树，每个根都代表一个历史版本。但为什么是每个根而不是每棵树呢 ( 因为这棵线段树没学多重影分身之术，它不喜欢多树运动 ) ？假如我们每次进行更新操作时都要先拷贝一份上次的版本用来回溯，再对原本的线段树进行修改，这样的话无论时间复杂度还是空间复杂度都是难以接受的。

因此，可持久化线段树横空出世！（鼓掌鼓掌）

当我们在修改关键值时，只有相关区间的节点内的值会受到影响，而树本身结构并未发生变化，那么在每次修改时，不再是在原来的版本上下功夫，而是创建一系列新的节点，从而达到可持久化的目的。

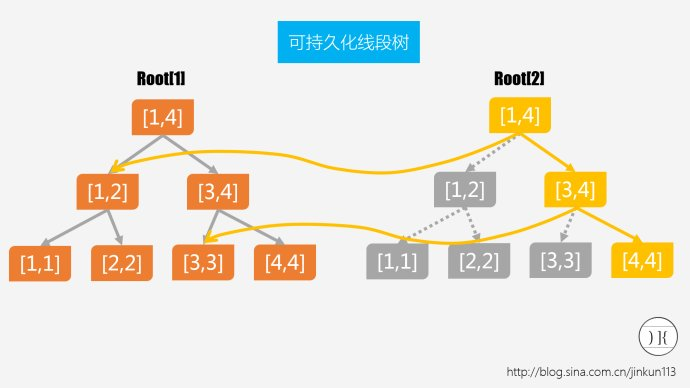
我在4处加了1（红色数字代表和）:

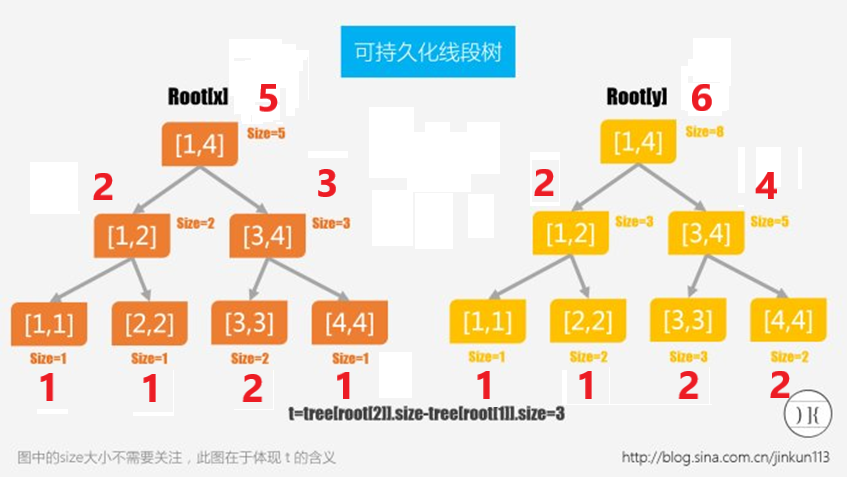
发现改变的只有一条链上的数据：

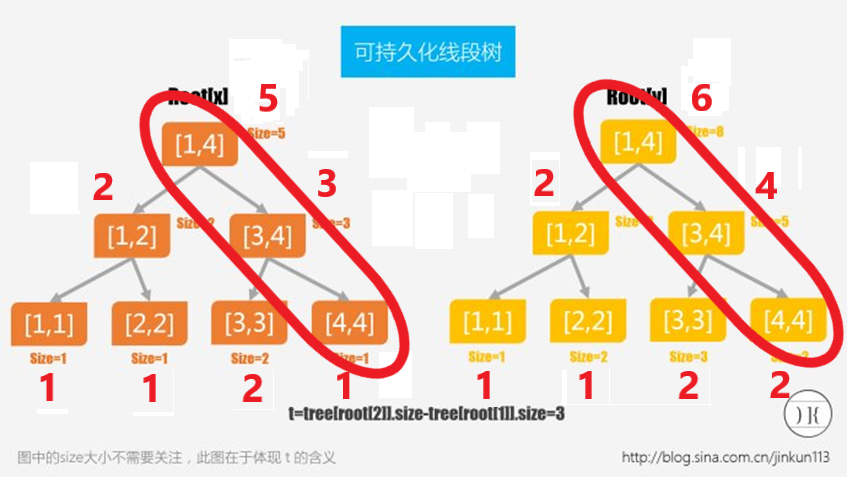
所以我们只需要多记录一条链就能代表历史的版本了：

离散化（求第k大/小需掌握）

就是把数据排序，然后用1，2，3...n来代表数据，从而与主席树结合解决问题。

for (int i = 1; i <= n; i++)
        {
            scanf("%d", &a[i]);
            b[i] = a[i];
        }
        std::sort(b+1, b+n+1);
        int m = std::unique(b+1, b+n+1)-b-1;
        for (int i = 1; i <= n; i++)
            a[i] = std::lower_bound(b+1, b+n+1, a[i])-b;

有了这些前置知识，主席树也不难理解了，接下来咱们通过例题逐步剖析主席树，看看它究竟是何方神圣。

HDU 2665 - Kth number

旅行传送门

Problem Description

Give you a sequence and ask you the kth big number of a inteval.

Input

The first line is the number of the test cases.
For each test case, the first line contain two integer n and m (n, m <= 100000), indicates the number of integers in the sequence and the number of the quaere.
The second line contains n integers, describe the sequence.
Each of following m lines contains three integers s, t, k.
[s, t] indicates the interval and k indicates the kth big number in interval [s, t]

Output

For each test case, output m lines. Each line contains the kth big number.

Sample Input

1 
10 1 
1 4 2 3 5 6 7 8 9 0 
1 3 2 

Sample Output

2

题目分析

首先，咱们分别定义一个左子树数组、右子树数组与权值数组，以及定义一个root数组，root数组用来保存各历史版本的根：

int root[MAXN], lson[MAXN<<5], rson[MAXN<<5], sum[MAXN<<5];

• root：每次进行插入操作时都会新生成一个根节点，储存的值为节点编号，下标代表第几个根节点(历史版本)，即root[i]为i版本的根编号
• lson：储存的值为左儿子的节点编号，下标代表父节点的编号，如lson[3] = 5表示3号节点的左儿子为5号节点
• rson：同lson
• sum：主席树最初是一棵空树，只不过其划分的不再是区间，而是值域，sum数组存储的信息表示该值域内有多少个数，其下标为节点编号。

 “‘主席树’是维护值域的，可持久化线段树是维护序列的；
 ‘主席树’是数字搜索树，也就是Trie一样的东西。”
 ——知乎RhmBWT 珂朵莉树之父

建树操作：

//建树，其实就是新建节点的过程，本题可以省去，在此加上是为了与线段树作比较，更利于读者对主席树的理解
int build(int l, int r)
{
    int rt = ++tot;
    sum[rt] = 0;
    if (l < r)
    {
        int mid = (l + r) >> 1;
        lson[rt] = build(l, mid);
        rson[rt] = build(mid + 1, r);
    }
    return rt;
}

更新操作（不加注释了，把下面的图解看完就懂了）：

假设主席树的上一个版本长这样（框外的数字代表该值域内有几个数，如[1,4] = 3表示有3个数在区间[1,4]内）：

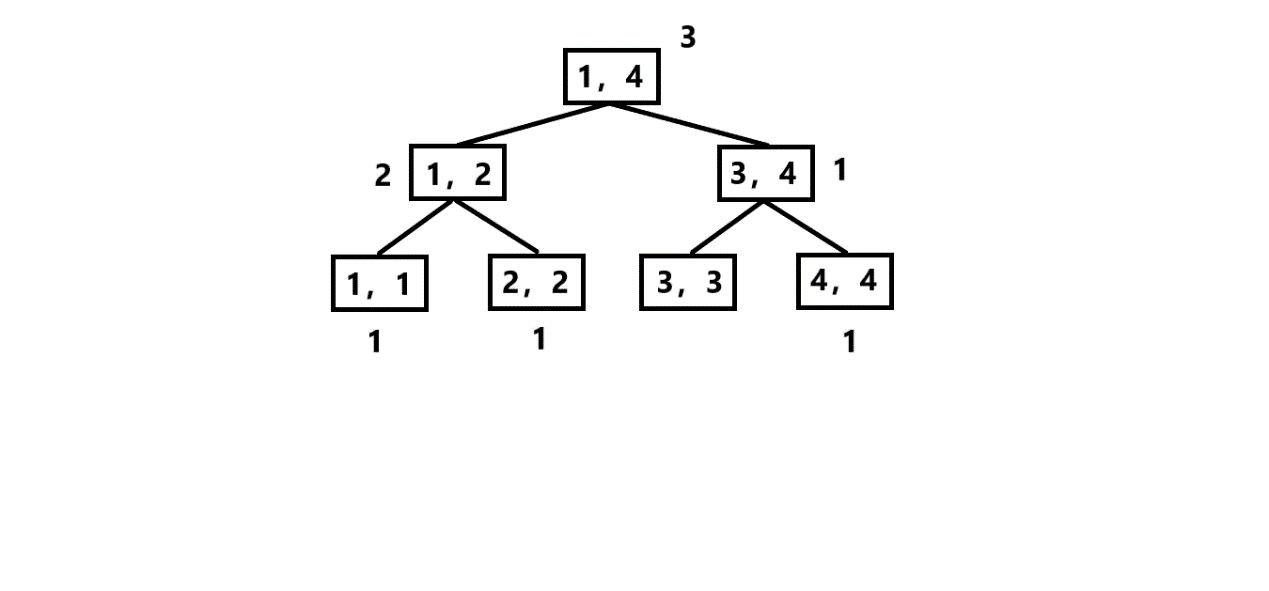
现在我们要插入3，先新建一个当前版本的新节点，它指向上个版本根节点的左右子树，同时3在值域[1,4]内，其sum值+1：

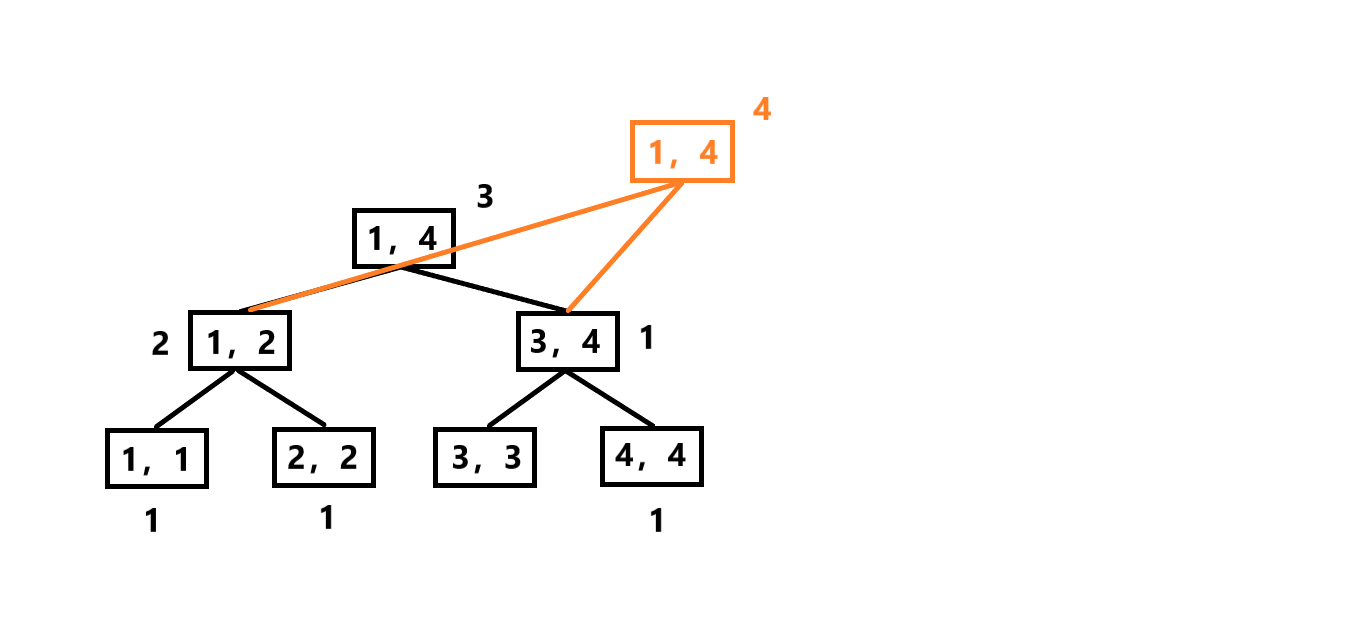
然后我们康康它的左右子树值域范围，显然3在右子树的值域内，那我们就新建一个右子树节点，相应节点的sum值也+1：

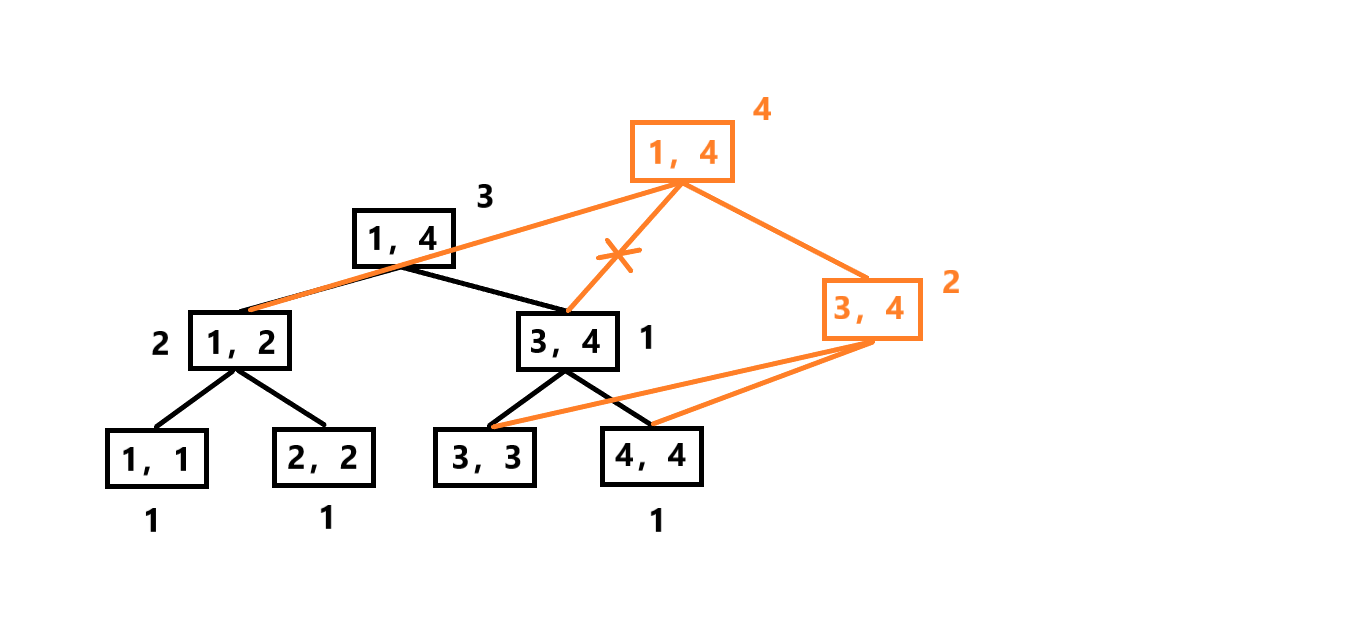
递归更新直至到达叶子节点，至此一次更新完成：

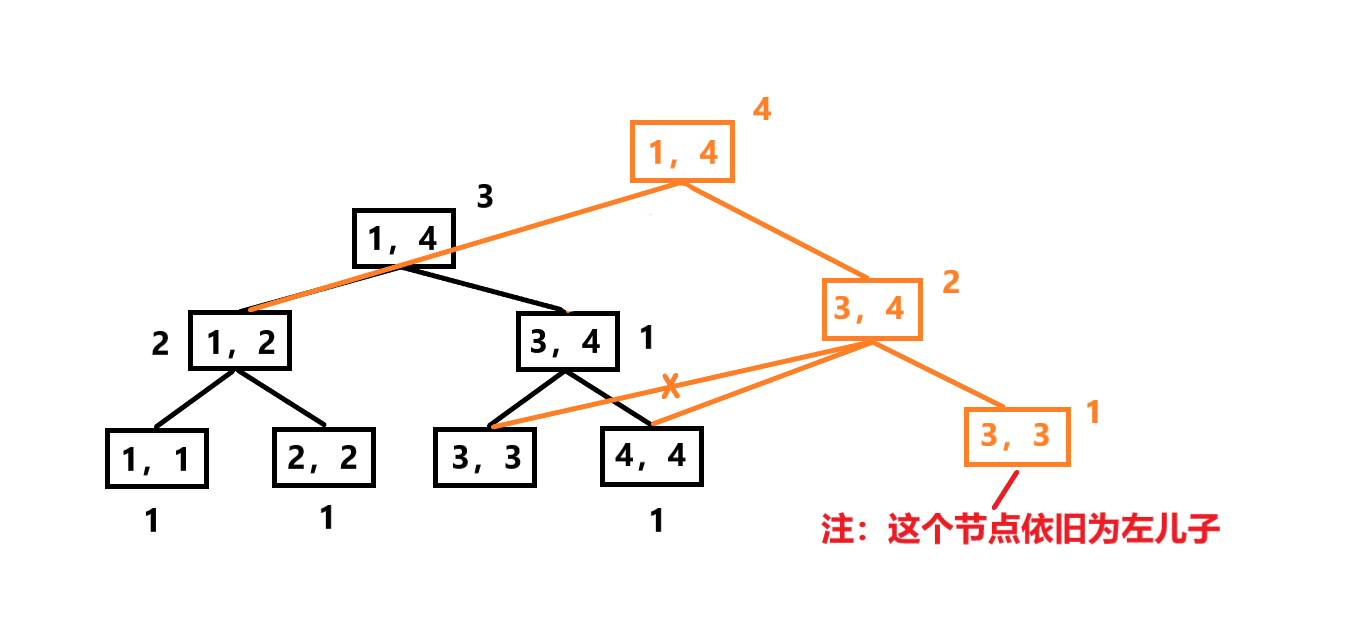
剩下的就看代码吧：

// p为前一个版本，rt是当前版本，每插入一个值，就建立一个新版本的根，并更新沿途的信息。
int update(int p, int l, int r, int x)
{
    int rt = ++tot;
    lson[rt] = lson[p], rson[rt] = rson[p], sum[rt] = sum[p] + 1;
    if (l < r)
    {
        int mid = (l + r) >> 1;
        if (x <= mid)
            lson[rt] = update(lson[rt], l, mid, x);
        else
            rson[rt] = update(rson[rt], mid + 1, r, x);
    }
    return rt;
}

查询操作：

运用前缀和的思想，如果要询问[l,r]的统计信息，只需要用[1,r]的信息减去[1,l-1]的信息就行了

• u 较前版本，即[1~l-1]
• v 较后版本，即[l~r]
• k 第k小

int query(int u, int v, int l, int r, int k)
{
   if (l == r)
       return l;
   int x = sum[lson[v]] - sum[lson[u]];
   int mid = (l + r) >> 1;
   /*
       两历史版本的左子树之差如果大于等于k，
       说明第k小个数在左半值域内，否则在右半值域内
       其实不难想，左边要至少有k个数，才谈得上有第k小
   */
   if (x >= k)
       return query(lson[u], lson[v], l, mid, k);
   else
       return query(rson[u], rson[v], mid + 1, r, k - x);
   /*
       右半值域所含数的个数相较左半值域少了x个，
       第k小也就随之变为第k - x小
       就像校队里比我弱的都退役了，
       那我不就是最弱的了吗(啊什么？我原本就是最弱的吗)
   */
}

关于空间问题，我们分析一下：由于我们是动态开点的，所以一棵线段树只会出现2n - 1个结点。然后，有n次修改，每次至多增加[\({log_2{n}}\)] + 1个结点。因此，最坏情况下n次修改后的结点总数会达到2n - 1 + n ([\({log_2{n}}\)] + 1)。 此题的 n <= \({10^5}\)，单次修改至多增加[\({log_2{10^5}}\)] + 1 = 18 个结点，故n次修改后的结点总数为 2 * 10 - 1 + 18 * \({10^5}\)，忽略掉-1，大概就是20 * \({10^5}\)。

最后给一个忠告：千万不要吝啬空间（大多数题目中空间限制都较为宽松，因此一般不用担心空间超限的问题）！保守一点，直接上个\({2^5}\) * \({10^5}\)接近原空间的两倍（即 n << 5）。

一般不用担心，当然也只是一般而已。。。

最后附上完整代码（代码简陋请见谅(/ω＼)）：

AC代码

#include <bits/stdc++.h>
#define rep(i, x, y) for (int i = (x); i <= (y); i++)
#define down(i, x, y) for (int i = (x); i >= (y); i--)
#define MAXN 100000 + 10

int a[MAXN], b[MAXN], root[MAXN], lson[MAXN << 5], rson[MAXN << 5], sum[MAXN << 5];
int st, ed, k;

inline int read()
{
    int x = 0, f = 1;
    char ch = getchar();
    while (ch < '0' || ch > '9')
    {
        if (ch == '-')
            f = -1;
        ch = getchar();
    }
    while (ch >= '0' && ch <= '9')
    {
        x = x * 10 + ch - '0';
        ch = getchar();
    }
    return x * f;
}

int build(int l, int r)
{
    int rt = ++tot;
    sum[rt] = 0;
    if (l < r)
    {
        int mid = (l + r) >> 1;
        lson[rt] = build(l, mid);
        rson[rt] = build(mid + 1, r);
    }
    return rt;
}

int update(int p, int l, int r, int x)
{
    int rt = ++tot;
    lson[rt] = lson[p], rson[rt] = rson[p], sum[rt] = sum[p] + 1;
    if (l < r)
    {
        int mid = (l + r) >> 1;
        if (x <= mid)
            lson[rt] = update(lson[rt], l, mid, x);
        else
            rson[rt] = update(rson[rt], mid + 1, r, x);
    }
    return rt;
}

int query(int u, int v, int l, int r, int k)
{
    if (l == r)
        return l;
    int x = sum[lson[v]] - sum[lson[u]];
    int mid = (l + r) >> 1;
    if (x >= k)
        return query(lson[u], lson[v], l, mid, k);
    else
        return query(rson[u], rson[v], mid + 1, r, k - x);
}

int main(int argc, char const *argv[])
{
    t = read();
    while (t--)
    {
        n = read(), m = read(), tot = 0;
        //离散化
        rep(i, 1, n)
            a[i] = b[i] = read();
        std::sort(b + 1, b + n + 1);
        int nn = std::unique(b + 1, b + n + 1) - b - 1;
        root[0] = build(1, m);
        rep(i, 1, n)
        {
            a[i] = std::lower_bound(b + 1, b + nn + 1, a[i]) - b;
            root[i] = update(root[i - 1], 1, nn, a[i]);
        }
        rep(i, 1, m)
        {
            st = read(), ed = read(), k = read();
            printf("%d\n", b[query(root[st - 1], root[ed], 1, nn, k)]);
        }
    }

    return 0;
}

彩蛋：

后排再次感谢lfw学长~