数据结构 -- 哈希表（hash table）

简介

　  哈希表（Hash table，也叫散列表），是根据关键码值(Key value)而直接进行访问的数据结构。也就是说，它通过把关键码值映射到表中一个位置来访问记录，以加快查找的速度。这个映射函数叫做散列函数，存放记录的数组叫做散列表。

　　记录的存储位置=f(关键字)

　　这里的对应关系f称为散列函数，又称为哈希（Hash函数），采用散列技术将记录存储在一块连续的存储空间中，这块连续存储空间称为散列表或哈希表（Hash table）。

　　哈希表hashtable(key，value)：

　　1. 把Key通过一个固定的算法函数既所谓的哈希函数转换成一个整型数字，

　　2. 然后就将该数字对数组长度进行取余，取余结果就当作数组的下标，

　　3. 将value存储在以该数字为下标的数组空间里。

　　　　

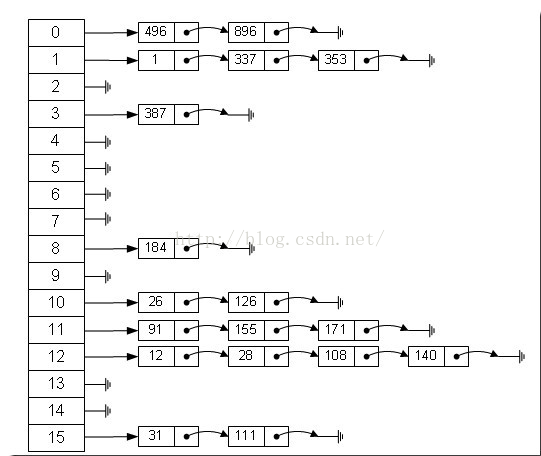
　　左边很明显是个数组，数组的每个成员包括一个指针，指向一个链表的头，当然这个链表可能为空，也可能元素很多。

　　我们根据元素的一些特征把元素分配到不同的链表中去，也是根据这些特征，找到正确的链表，再从链表中找出这个元素。

　　Hash Table的查询速度非常的快，几乎是O(1)的时间复杂度。hash就是找到一种数据内容和数据存放地址之间的映射关系。

　　 散列法：元素特征转变为数组下标的方法。

---

 

哈希冲突

　　哈希化之后难免会产生一个问题，那就是对不同的关键字，可能得到同一个散列地址，即同一个数组下标，这种现象称为哈希冲突。

　　那么我们该如何去处理冲突呢？

　　1. 开放地址法：通过系统的方法找到数组的另一个空位，把数据填入，而不再用哈希函数得到的数组下标，因为该位置已经有数据了；

　　2. 链地址法：  创建一个存放链表的数组，数组内不直接存储数据，这样当发生冲突时，新的数据项直接接到这个数组下标所指的链表中。

　　3. 公共溢出区法：建立一个特殊存储空间，专门存放冲突的数据。此种方法适用于数据和冲突较少的情况。

　　4. 再散列法（再哈希法）：准备若干个hash函数，如果使用第一个hash函数发生了冲突，就使用第二个hash函数，第二个也冲突，使用第三个……

---

Hash函数　

　　hash地址冲突几率，与hash函数密切相关。以下我们看下常用的计算hash地址的函数

　　（A）直接定址法

　　　　取关键字或者关键字的某个线性函数作为Hash地址，即address(key) = a*key + b; 如果知道学生的学号是从2000开始，最大为4000，则可以将address(key) =key-2000作为Hash地址。

　　（B）平方取中法

　　　　对关键字进行平方计算，然后取结果的中间几位作为Hash地址，假如有以下关键字序列{421，423，436}，平方之后的结果为{177241，178929，190096}，那么可以取中间的两位数{72，89，00}作为Hash地址。

　　（C）折叠法

　　　　将关键字拆分成几个部分，然后将这几个部分组合在一起，以特定的方式进行转化形成Hash地址。例如假如知道某图书的SBN号为：8903-241-23，可以将address(key)=89+03+24+12+3作为Hash地址。

　　（D）除留取余法

　　　　如果知道Hash表的最大长度为m，可以取不大于m的最大质数p，然后对关键字进行取余运算，address(key)=key % p。

自定义代码示例

import java.util.TreeMap;

public class MyHashTable<K, V> {

    private static final int upperTol = 10;
    private static final int lowerTol = 2;
    private static final int initCapacity = 7;

    private TreeMap<K, V>[] hashtable;
    private int m;
    private int size;

    public MyHashTable(int m){
        this.m = m;
        size = 0;
        hashtable = new TreeMap[m];
        for (int i = 0; i < m ; i ++){
            hashtable[i] = new TreeMap<>();
        }
    }

    public MyHashTable(){
        this(initCapacity);
    }

    private int hash(K key){
        return (key.hashCode() & 0x7fffffff) % m;
    }

    public int getSize(){
        return size;
    }

    public void add(K key, V value){
        TreeMap<K, V> map = hashtable[hash(key)];
        if (map.containsKey(key)){
            map.put(key, value);
        }else {
            map.put(key, value);
            size ++;

            if (size >= upperTol * m){
                resize(2 * m); //扩容
            }
        }
    }

    public V remove(K key){
        TreeMap<K, V> map = hashtable[hash(key)];
        V ret = null;
        if (map.containsKey(key)){
            ret = map.remove(key);
            size --;

            if (size < lowerTol * m && m / 2 >=initCapacity){
                resize( m/2 ); //缩容
            }
        }
        return ret;
    }

    public void set(K key, V value){
        TreeMap<K, V> map = hashtable[hash(key)];
        if (!map.containsKey(key)){
           throw new IllegalArgumentException(key + "doesn't exist!");
        }
        map.put(key, value);
    }

    public V get(K key){
        return hashtable[hash(key)].get(key);
    }

    public boolean contains(K key){
        return hashtable[hash(key)].containsKey(key);
    }

    private void resize(int newM){
        TreeMap<K, V>[] newHashTable = new TreeMap[newM];
        for (int i = 0; i < newM; i++){
            newHashTable[i] = new TreeMap<>();
        }

        int oldM = m;
        this.m = newM;
        for (int i = 0; i < oldM; i++){
            TreeMap<K, V> map = hashtable[i];
            for (K key : map.keySet()){
                newHashTable[hash(key)].put(key, map.get(key));
            }
        }
        this.hashtable = newHashTable;
    }
}

 

 

 

 

参考：https://blog.csdn.net/eson_15/article/details/51138588 https://www.jianshu.com/p/5a2a5f6de440