数据结构 -- 红黑树
前言
在我们学习红黑树之前,我们先来看看什么是2-3树
2-3树
2-3树是最简单的B-树(或-树)结构,其每个非叶节点都有两个或三个子女,而且所有叶都在统一层上。
2-3树是一种平衡搜索树。但2-3树已经不是一棵二叉树了,因为2-3树允许存在3这种节点,3节点中可以存放两个元素,并且可以有三个子节点。
定义: 1. 一个节点保存一个值,这样的节点在2 - 3树中成为2- 节点。2- 节点,含有一个键(及其对应的值)和两条链接。该节点的左链接小于该节点的键;该节点的右链接大于该节点的键
2. 一个节点保存两个值,这样的节点在2 - 3树中成为3- 节点。3- 节点,含有两个键(及其对应的值)和三条链接。左链接小于该节点的左键;中链接在左键和右键之间;右链接大于该节点右键
如下图,是一棵 完美平衡的2-3树
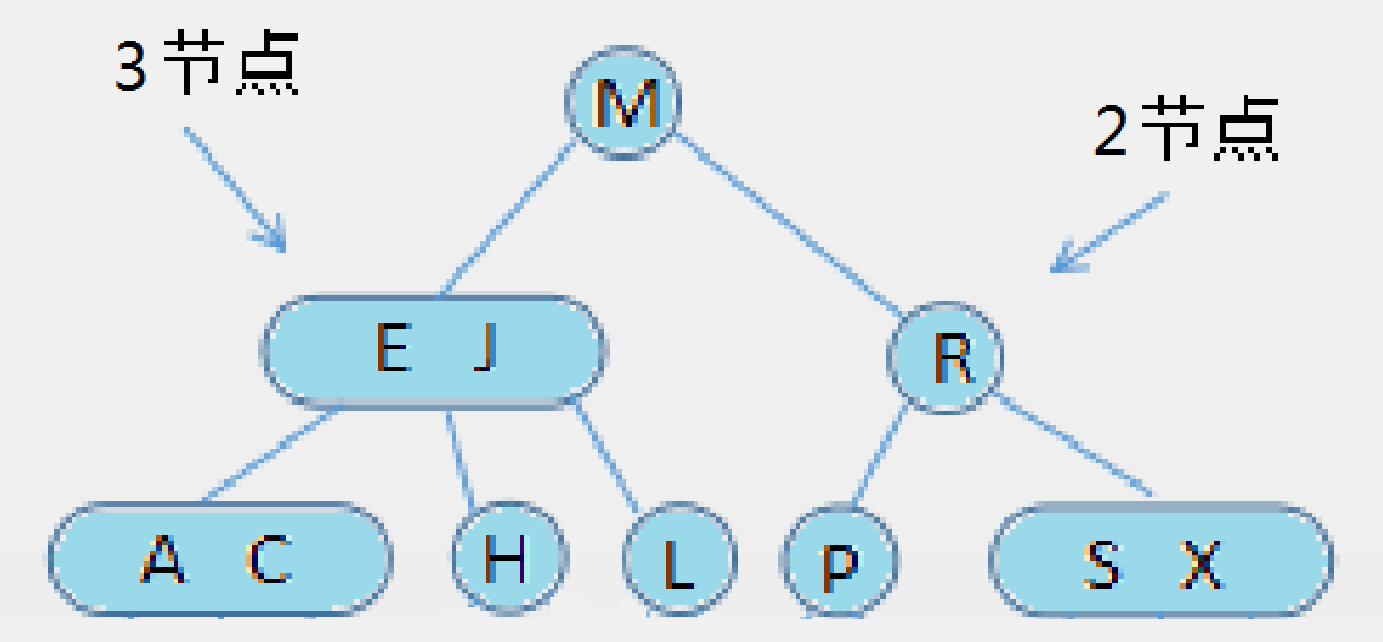
那2-3树是如何维持绝对平衡的呢?我们通过图形解释
向2节点中插入新建内容 向一棵只含有一个3-结点的树中插入新键

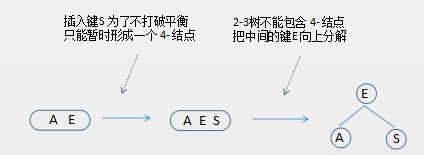
向一个父结点为 2- 结点的 3- 结点插入新键 向一个父结点为3- 结点的 3- 结点中插入新键
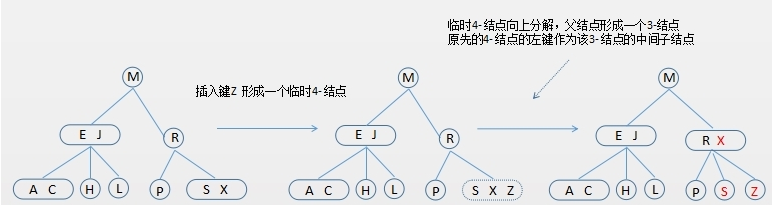

一个临时4节点分解为一棵2-3树6种情况
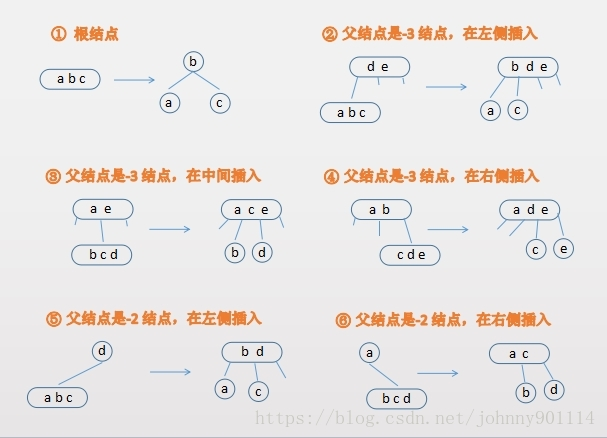
完美平衡的2-3树和红黑树的对应关系
红黑树其实是2-3树的一种只含2节点的表现形式。还是二叉树节点大于左子节点,小于右子节点。我们把2-3树中的2节点用黑色表示,3节点用红色表示(3节点的左节点为红色、右节点为黑色)
将2-3树的链接定义为两种类型:黑链接、红链接
黑链接:是2-3树中普通的链接,可以把2-3树中的 2- 结点 与它的子结点之间的链当作黑链接
红链接:2-3树中 3- 结点分解成两个 2- 结点,这两个 2- 结点之间的链接就是红链接
那么如何将2-3树和红黑树等价起来,我们规定:红链接均为左链接
根据上面对完美平衡的2-3树和红链接的介绍可以得出结论:没有一个结点同时和两个红链接相连
根据上面对完美平衡的2-3树和黑链接的介绍可以得出结论:完美平衡的2-3树是保持完美黑色平衡的,任意空链接到根结点的路径上的黑链接数量相等
黑节点:2-3树中普通的 2-结点 的颜色
红节点:2-3树中 3-结点 分解出两个 2-结点 的最小 2-结点
2-3树与红黑树对应图
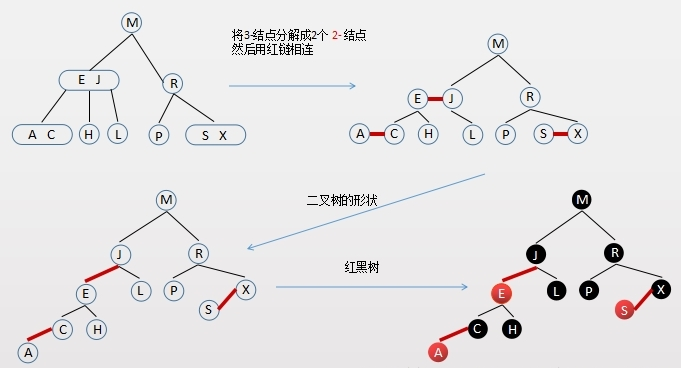
红黑树(RedBlackTree)
特征: 1.节点都有颜色;
2.在插入和删除的过程中,要遵循保持这些颜色的不同排列的规则;
3. 插入节点的颜色是红色;
4. 保持黑色平衡。
性质:1. 每个结点要么是红色,要么是黑色;
2. 根节点是黑色的;
3. 每个叶子节点(最后的空节点)是黑色的;
4. 如果一个节点是红色的,那么他的孩子节点是黑色的;
5. 从任一节点到其每个叶子的所有路径都包含相同数目的黑色节点。
在红-黑树中插入的节点都是红色的,这不是偶然的,因为插入一个红色节点比插入一个黑色节点违背红-黑规则的可能性更小。
原因是:插入黑色节点总会改变黑色高度(违背规则5),但是插入红色节点只有一半的机会会违背规则4。另外违背规则4比违背规则5要更容易修正。
平衡性的修正
(A)颜色翻转
为什么要颜色翻转(flipColor)?在插入的过程中可能出现如下情况:两个左右子结点都是红色
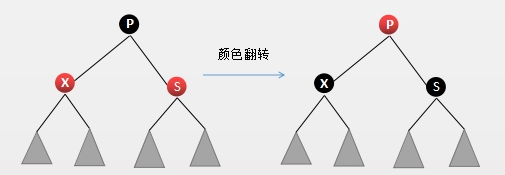
根据我们上面的描述,红链只允许是左链(也就是左子结点是红色) 所以需要进行颜色转换:把该结点的左右子结点设置为黑色,自己设置为红色
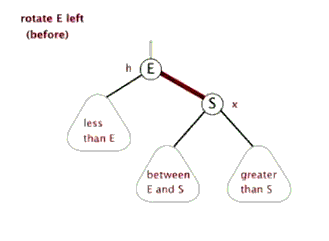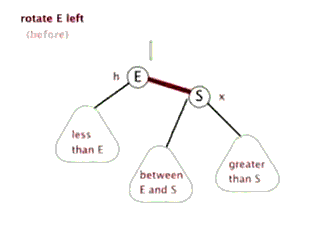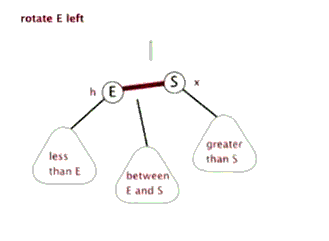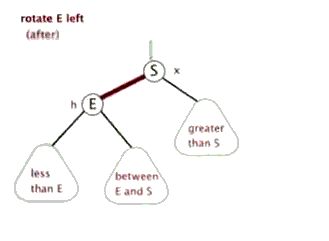
(B)左旋转
1. 右孩子节点颜色是红色。
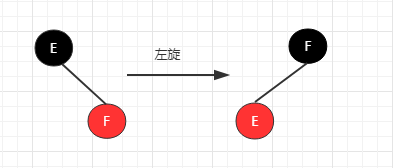
2. 颜色翻转后,父节点的右孩子颜色变成红色,其实是和第一种情况一样,都是右节点是红色时进行左旋转
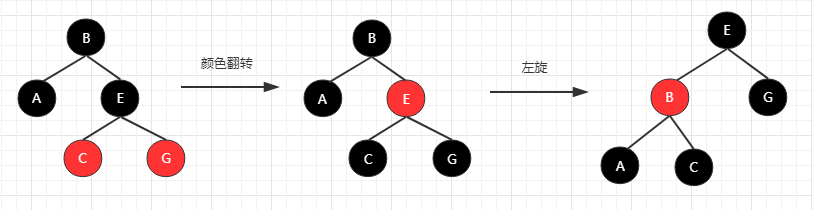
(C)右旋转
连续出现两个左红色链接
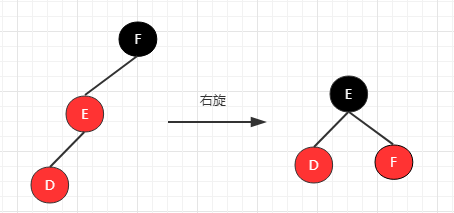
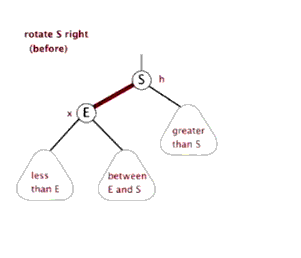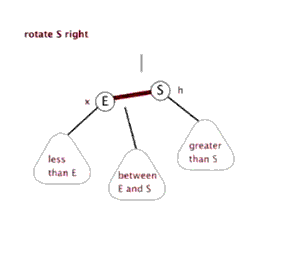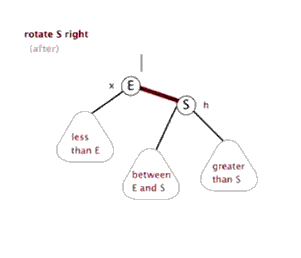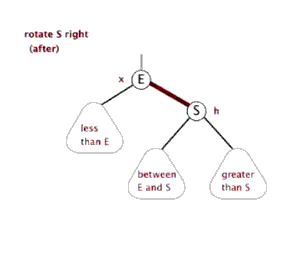
由上面所述说的三种维持平衡方式可知。我们在插入的时候,只要满足不出现 两个连续左红色链接、右红色链接、左右都是红色链接 的情况就可以了。
所以仅仅需要处理三种情况即可:
1. 如果出现右侧红色链接,需要左旋
2. 如果出现两个连续的左红色链接,需要右旋
3. 如果结点的左右子链接都是红色,需要颜色翻转
我们综合一下操作,稍微复杂,但离不开上面三个情况,如图
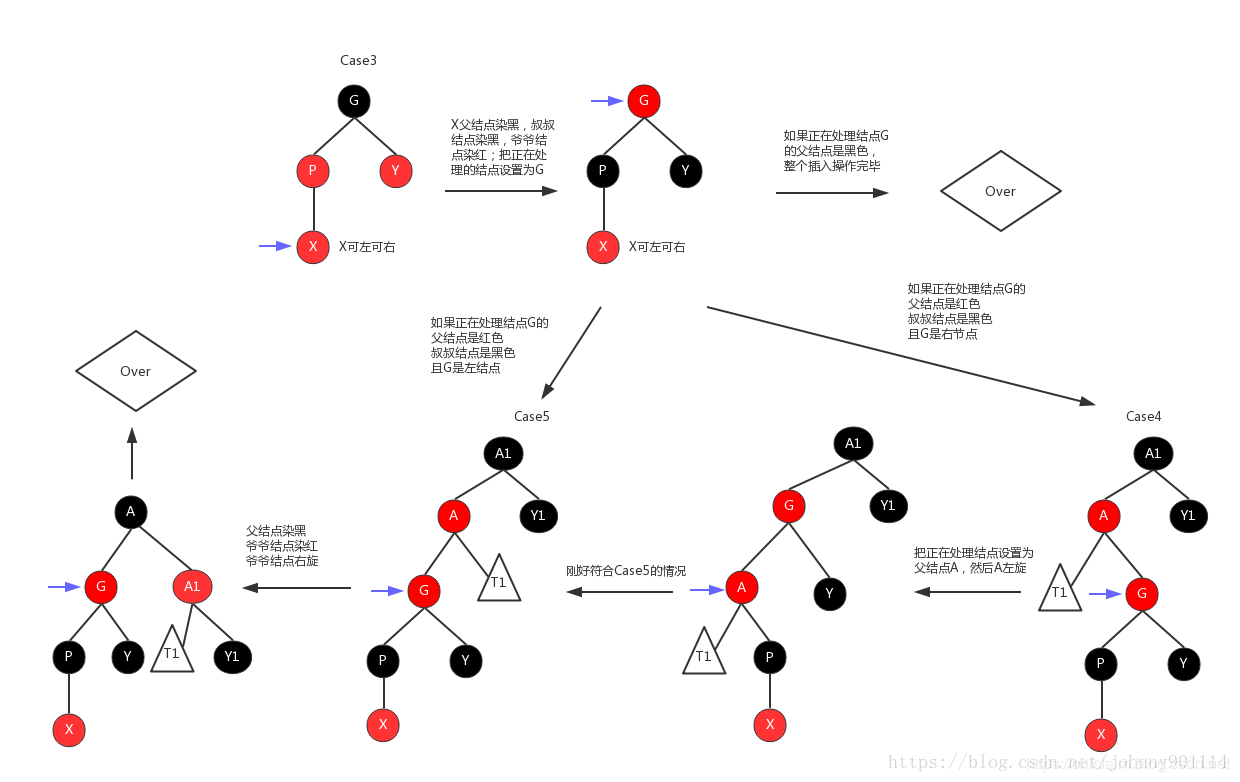
代码实现
/** * 红黑树实现 * @param <K> * @param <V> */ public class RBTree<K extends Comparable<K>,V> { private static final boolean RED = true; //红节点 private static final boolean BLACK = false; //黑节点 private class Node{ public K key; public V value; public Node left, right; public boolean color; public Node(K key, V value){ this.key = key; this.value = value; left = null; right = null; color = RED; } } private Node root; private int size; public RBTree(){ root = null; size = 0; } public int getSize(){ return size; } public boolean isEmpty(){ return size == 0; } //判断node的节点颜色 private boolean isRed(Node node){ if (node == null){ return BLACK; } return node.color; } //左旋转 private Node leftRotate(Node node){ Node x = node.right; //左旋转 node.right = x.left; x.left = node; x.color = node.color; node.color = RED; return x; } //右旋转 private Node rightRotate(Node node){ Node x = node.left; //右旋转 node.left = x.right; x.right = node; x.color = node.color; node.color = RED; return x; } //颜色翻转 private void flipColors(Node node){ node.color = RED; node.left.color = BLACK; node.right.color = BLACK; } // 向红黑树中添加新的元素(key, value) public void add(K key, V value){ root = add(root, key, value); root.color = BLACK; //最终根节点为黑色节点 } // 向以node为根的红黑树中插入元素(key, value),递归算法 // 返回插入新节点后红黑树的根 private Node add(Node node, K key, V value){ if(node == null){ size ++; return new Node(key, value); //默认插入红色节点 } if(key.compareTo(node.key) < 0) node.left = add(node.left, key, value); else if(key.compareTo(node.key) > 0) node.right = add(node.right, key, value); else // key.compareTo(node.key) == 0 node.value = value; //当前节点的右孩子是红色, 左孩子不是红色。进行左旋转 if(isRed(node.right) && !isRed(node.left)){ node = leftRotate(node); } //当前节点的左孩子和左孩子的左孩子 都是红色.出现连续的红色节点 进行右旋转 if(isRed(node.left) && isRed(node.left.left)){ node = rightRotate(node); } //当前节点的左右孩子都是红色。进行颜色翻转 if (isRed(node.left) && isRed(node.right)){ flipColors(node); } return node; } // 返回以node为根节点的二分搜索树中,key所在的节点 private Node getNode(Node node, K key){ if(node == null) return null; if(key.equals(node.key)) return node; else if(key.compareTo(node.key) < 0) return getNode(node.left, key); else // if(key.compareTo(node.key) > 0) return getNode(node.right, key); } public boolean contains(K key){ return getNode(root, key) != null; } public V get(K key){ Node node = getNode(root, key); return node == null ? null : node.value; } public void set(K key, V newValue){ Node node = getNode(root, key); if(node == null) throw new IllegalArgumentException(key + " doesn't exist!"); node.value = newValue; } // 返回以node为根的二分搜索树的最小值所在的节点 private Node minimum(Node node){ if(node.left == null) return node; return minimum(node.left); } // 删除掉以node为根的二分搜索树中的最小节点 // 返回删除节点后新的二分搜索树的根 private Node removeMin(Node node){ if(node.left == null){ Node rightNode = node.right; node.right = null; size --; return rightNode; } node.left = removeMin(node.left); return node; } // 从二分搜索树中删除键为key的节点 public V remove(K key){ Node node = getNode(root, key); if(node != null){ root = remove(root, key); return node.value; } return null; } private Node remove(Node node, K key){ if( node == null ) return null; if( key.compareTo(node.key) < 0 ){ node.left = remove(node.left , key); return node; } else if(key.compareTo(node.key) > 0 ){ node.right = remove(node.right, key); return node; } else{ // key.compareTo(node.key) == 0 // 待删除节点左子树为空的情况 if(node.left == null){ Node rightNode = node.right; node.right = null; size --; return rightNode; } // 待删除节点右子树为空的情况 if(node.right == null){ Node leftNode = node.left; node.left = null; size --; return leftNode; } // 待删除节点左右子树均不为空的情况 // 找到比待删除节点大的最小节点, 即待删除节点右子树的最小节点 // 用这个节点顶替待删除节点的位置 Node successor = minimum(node.right); successor.right = removeMin(node.right); successor.left = node.left; node.left = node.right = null; return successor; } } }
红黑树的查找、插入和删除时间复杂度都为O(log2N),额外的开销是每个节点的存储空间都稍微增加了一点,因为一个存储红黑树节点的颜色变量。
插入和删除的时间要增加一个常数因子,因为要进行旋转,平均一次插入大约需要一次旋转,因此插入的时间复杂度还是O(log2N),(时间复杂度的计算要省略常数),但实际上比普通的二叉树是要慢的。
大多数应用中,查找的次数比插入和删除的次数多,所以应用红黑树取代普通的二叉搜索树总体上不会有太多的时间开销。而且红黑树的优点是对于有序数据的操作不会慢到O(N)的时间复杂度。
参考:https://blog.csdn.net/johnny901114/article/details/81046088 https://www.cnblogs.com/ysocean/p/8004211.html



