数据结构 -- 线段树

 一、什么是线段树

　　线段树是一种二叉搜索树,与区间树相似,它将一个区间划分成一些单元区间,每个单元区间对应线段树中的一个叶结点。

　　对于线段树中的每一个非叶子节点[a,b],它的左儿子表示的区间为[a,(a+b)/2],右儿子表示的区间为[(a+b)/2+1,b]。

　　使用线段树可以快速的查找某一个节点在若干条线段中出现的次数，时间复杂度为O(logN)。

　　

　　线段树的思想和分治思想很相像。

　　线段树的每一个节点都储存着一段区间[L…R]的信息，其中叶子节点L=R。

　　它的大致思想是：将一段大区间平均地划分成2个小区间，每一个小区间都再平均分成2个更小区间……以此类推，直到每一个区间的L等于R（这样这个区间仅包含一个节点的信息，无法被划分）。

　　通过对这些区间进行修改、查询，来实现对大区间的修改、查询。这样一来，每一次修改、查询的时间复杂度都只为O(log2n)。

　　但是，可以用线段树维护的问题必须满足区间加法，否则是不可能将大问题划分成子问题来解决的.

　　什么是区间加法：一个问题满足区间加法，仅当对于区间[L,R]的问题的答案可以由[L,M]和[M+1,R]的答案合并得到。

二、线段树的基本内容　　

　　不要觉得线段树只是为了解决区间问题的数据结构，事实上，是线段树多用于解决区间问题，并不是线段树只能解决区间问题，首先，我们得先明白几件事情。

　　线段树主要是把一段大区间平均地划分成两段小区间进行维护，再用小区间的值来更新大区间。

　　这样既能保证正确性，又能使时间保持在log级别（因为这棵线段树是平衡的）。也就是说，一个[L…R]的区间会被划分成[L…(L+R)/2]和[(L+R)/2+1…R]这两个小区间进行维护，直到L=R。

　　如图所示：

　　　　

 

 

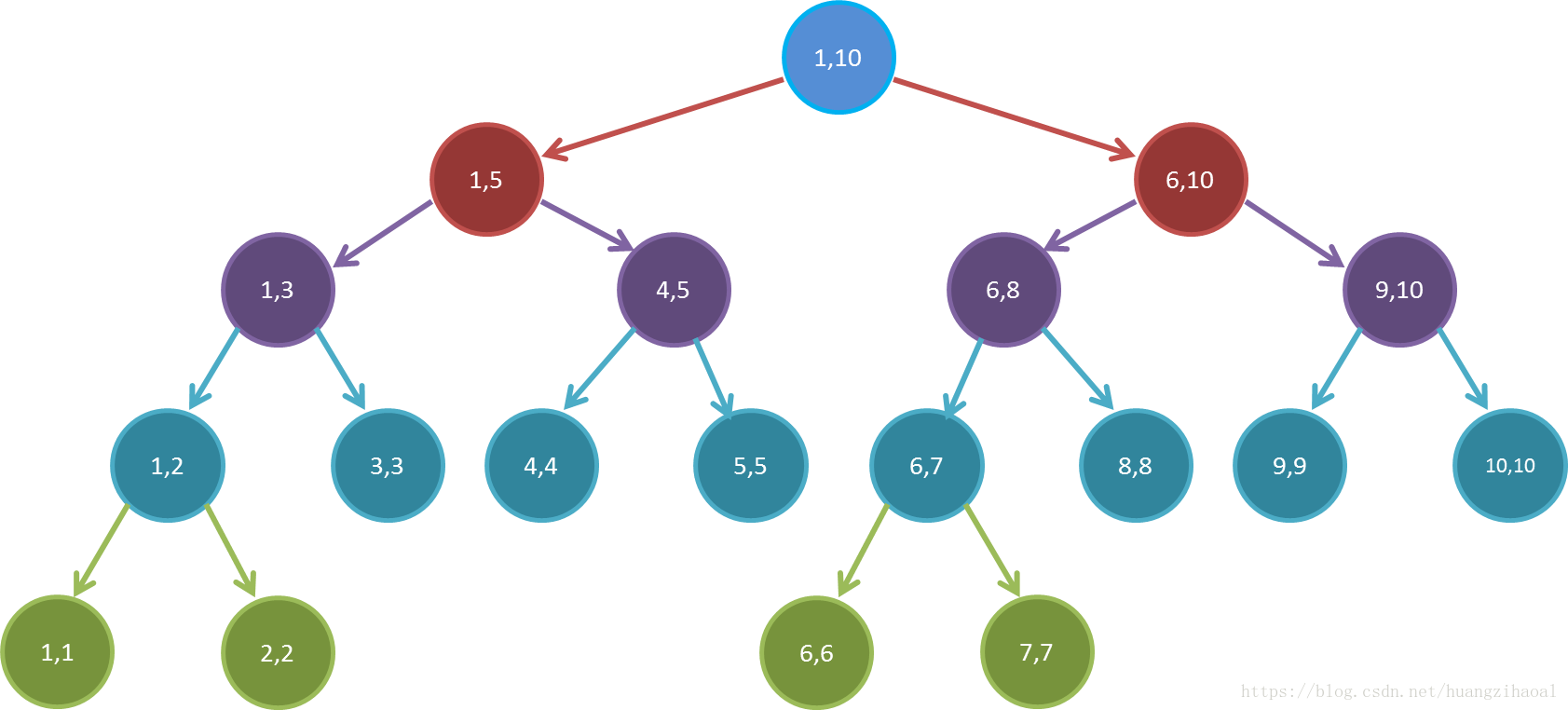
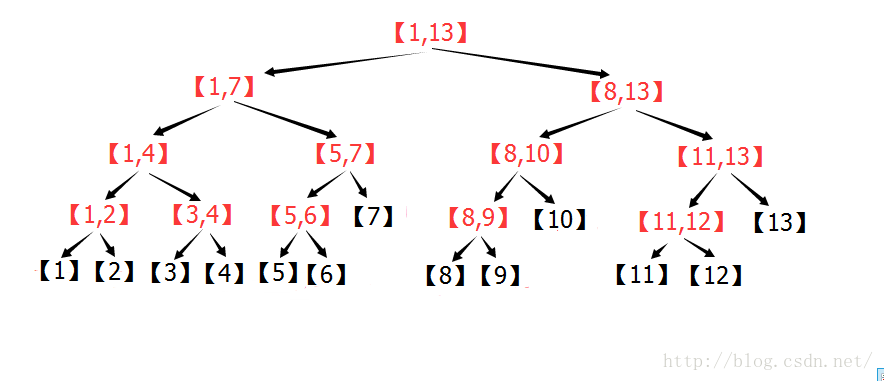
 　　可以发现，每个叶子结点的值就是数组的值，每个非叶子结点的度都为二，且左右两个孩子分别存储父亲一半的区间。每个父亲的存储的值也就是两个孩子存储的值的最大值。

　　 仔细观察每个父亲和孩子下标的关系，不难发现，每个左子树的下标都是偶数，右子树的下标都是奇数且为左子树下标+1，而且不难发现以下规律

• • l = fa*2 （左子树下标为父亲下标的两倍）
  • r = fa*2+1（右子树下标为父亲下标的两倍+1）

　　一般会开到4*n的空间防止RE。

 

三、相关代码

//线段树
public class SegmentTree<E> {
    private E[] tree;
    private E[] data;
    private Merger<E> merger;

    public SegmentTree(E[] arr, Merger<E> merger){
        this.merger = merger;

        data = (E[]) new Object[arr.length];
        for (int i = 0; i< arr.length; i++){
            data[i] = arr[i];
        }

        tree = (E[]) new Object[4 * arr.length];
        buildSegmentTree(0,0,data.length - 1);
    }
    //创建线段树
    private void buildSegmentTree(int treeIndex, int l, int r){
        if (l == r){
            tree[treeIndex] = data[r];
            return;
        }
        //当前节点的左孩子节点
        int leftTreeIndex = leftChild(treeIndex);
        //当前节点的右孩子节点
        int rightTreeIndex = rightChild(treeIndex);
        //区间中间节点索引
        int mid = l + (r - l) / 2;
        //从中间向左区间创建线段树
        buildSegmentTree(leftTreeIndex, l, mid);
        //从中间向右区间创建线段树
        buildSegmentTree(rightTreeIndex, mid + 1, r);

        tree[treeIndex] = merger.merge(tree[leftTreeIndex], tree[rightTreeIndex]);
    }

    public int getSize(){
        return data.length;
    }

    public E get(int index){
        if (index < 0 || index >= data.length){
            throw new IllegalArgumentException("Index is illegal.");
        }
        return data[index];
    }
    //返回完全二叉树的数组表示中，一个索引所表示的元素的左孩子节点的索引
    private int leftChild(int index){
        return 2 * index + 1;
    }
    //返回完全二叉树的数组表示中，一个索引所表示的元素的右孩子节点的索引
    private int rightChild(int index){
        return 2 * index + 2;
    }
    //返回区间[queryL， queryR]的值
    public E query(int queryL, int queryR){
        if (queryL < 0 || queryR >= data.length || queryR < 0 || queryR >= data.length || queryL > queryR){
            throw new IllegalArgumentException("Index is illegal.");
        }
        return query(0,0,data.length - 1, queryL, queryR);
    }

    //在以treeIndex为根节点的线段树中[l...r]的范围里，搜索区间[queryL...queryR]的值
    private E query(int treeIndex, int l, int r, int queryL, int queryR){
        if (l == queryL && r == queryR){
            return tree[treeIndex];
        }
        int mid = l + (r - l) / 2;
        int leftTreeIndex = leftChild(treeIndex);
        int rightTreeIndex = rightChild(treeIndex);
        //当查询的左区间大于中间值，则查询的内容不会在区间的左边
        if (queryL >= mid + 1){
            return query(rightTreeIndex, mid + 1, r, queryL, queryR);
        }else if (queryR <= mid){//同理，当查询的右区间小于中间值，则查询的内容不会在区间的右边
            return query(leftTreeIndex, l, mid, queryL, queryR);
        }
        //当查询的内容一部分在左，一部分在右时，指定范围查询。
        E leftResult = query(leftTreeIndex, l, mid, queryL, mid);
        E rightResult = query(rightTreeIndex, mid + 1, r, mid + 1, queryR);
        return merger.merge(leftResult, rightResult);
    }

    //将index位置的值，更新为e
    public void set(int index, E e){
        if (index < 0 || index >= data.length){
            throw new IllegalArgumentException("Index is illegal.");
        }
        data[index] = e;
        set(0,0,data.length - 1, index, e);
    }

    //在以treeIndex为根的线段树中更新index的值为e
    private void set(int treeIndex, int l, int r, int index, E e){
        if (l == r){
            tree[treeIndex] = e;
            return;
        }

        int leftTreeIndex = leftChild(treeIndex);
        int rightTreeIndex = rightChild(treeIndex);
        int mid = l + (r - l) / 2;
        //修改的节点索引大于中间索引，向右边线段树查找更新
        if (index >= mid + 1){
            set(rightTreeIndex, mid + 1, r, index, e);
        }else {//否则就是修改的节点索引小于中间索引，向左边线段树查找更新
            set(leftTreeIndex, l, mid, index, e);
        }
        merger.merge(tree[leftTreeIndex], tree[rightTreeIndex]);
    }
    @Override
    public String toString() {
        StringBuilder stringBuilder = new StringBuilder();
        stringBuilder.append("[");
        for (int i=0; i< tree.length; i++){
            if (tree[i] != null){
                stringBuilder.append(tree[i]);
            }else {
                stringBuilder.append("null");
            }
            if (i != tree.length - 1){
                stringBuilder.append(", ");
            }
        }
        stringBuilder.append("]");
        return stringBuilder.toString();
    }
}

public interface Merger<E> {
    E merge(E a, E b);
}

 

 待更新