P7745 [COCI2011-2012#3] ROBOT

Description

在一个平面直角坐标系中，有一个点 bot，现有四个指令，分别可以让 bot 向上、下、左、右四个方向中的一个移动一格。同时还有 \(n\) 个固定点，求每次移动后这些点到 bot 的哈曼顿距离之和。

两个点 \((x1, y1)\) 和 \((x2, y2\) 的曼哈顿距离为 \(|x1 - x2| + |y1 - y2|\)。

Solution

40 pts

每次移动后暴力求出每个点的哈曼顿距离，相加输出即可。

code

#include <bits/stdc++.h>
#define N 100005
#define int long long
using namespace std;
namespace xycyx {
	int n, m;
	int hmd[N];
	int X[N], Y[N];
	char c;
	int botx = 0, boty = 0;
	int get_hmd(int X1, int Y1) {
		return abs(X1 - botx) + abs(Y1 - boty);
	}
	void solve() {
		ios::sync_with_stdio();
		cin.tie(0);
		cin >> n >> m;
		for (int i = 1; i <= n; i++) cin >> X[i] >> Y[i];
		for (int i = 1; i <= m; i++) {
			cin >> c;
			if (c == 'S') boty++;
			if (c == 'J') boty--;
			if (c == 'I') botx++;
			if (c == 'Z') botx--;
			int ans = 0;
			for (int i = 1; i <= n; i++)
				ans += get_hmd(X[i], Y[i]);
			cout << ans << '\n';
		}
	}
}
signed main() {
	xycyx::solve();
	return 0;
} //40pts

100 pts

鉴于数据范围，时间复杂度应为 \(O(m)\)，故每次查询的时间复杂度都为 \(O(1)\)。

对于两条坐标轴，每次移动后分别二分求出有多少个点小于当前机器人的位置，多少点大于当前机器人的位置，求出当前移动对答案的贡献。直接更新答案并输出即可。

考虑一下每次移动造成的影响：

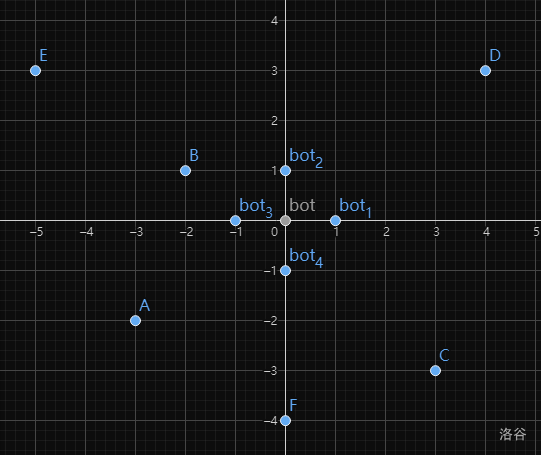
如果执行 S 操作，则意味着 bot 会从 移动到 \((0, 1)\) 的位置，此时明显的，对于 \(y \le y_{bot}\) 的 A、C、F 三点，哈曼顿距离分别加一；而对于 \(y > y_{bot}\) 的 B、D、E 三点而言，哈曼顿距离分别减一。即 \(y_i \le y_{bot}\) 的点在 S 操作时哈曼顿距离会增加，而 \(y_i > y_{bot}\) 的点在 S 操作时哈曼顿距离会减小。此时，答案的更新操作应为：减去移动前 \(y \le y_{bot}\) 的点的数量，加上当前 \(y \le y_{bot}\) 的点的数量。

对于剩余的三种操作同理。

可以使用 upper_bound 和 lower_bound。

code

注意先排序后再二分查找。

#include <bits/stdc++.h>
#define N 100000
#define M 300000
#define ll long long
using namespace std;
namespace cyxyc {
	int n, m;
	int X1, Y1, X2, Y2, X = 0, Y = 0;
	ll ans = 0;
	int x[N + 5], y[N + 5];
	char c[M + 5];
	int get_hmd(int x, int y) {
		return abs(x) + abs(y);
	}
	void solve() {
		ios::sync_with_stdio();
		cin.tie(0);
		cin >> n >> m;
		for (int i = 1; i <= n; i++) {
			cin >> x[i] >> y[i];
			ans += get_hmd(x[i], y[i]);
		}
		cin >> c + 1;
		sort(x + 1, x + n + 1), sort(y + 1, y + n + 1); //upper_bound 和 lower_bound 都是二分查找
		X1 = upper_bound(x + 1, x + n + 1, X) - (x + 1); //第一个大于当前位置的点的下标
		X2 = lower_bound(x + 1, x + n + 1, X) - (x + 1); //第一个大于等于当前位置的点的下标
		Y1 = upper_bound(y + 1, y + n + 1, Y) - (y + 1);
		Y2 = lower_bound(y + 1, y + n + 1, Y) - (y + 1);
		for (int i = 1; i <= m; i++) {
			if (c[i] == 'S') {
				ans += 2 * Y1 - n; //ans = ans - (n - Y1) + Y1
				Y++;
				Y1 = upper_bound(y + 1, y + n + 1, Y) - (y + 1);
				Y2 = lower_bound(y + 1, y + n + 1, Y) - (y + 1);
			}
			if (c[i] == 'J') {
				ans += n - 2 * Y2;
				Y--;
				Y1 = upper_bound(y + 1, y + n + 1, Y) - (y + 1);
				Y2 = lower_bound(y + 1, y + n + 1, Y) - (y + 1);
			}
			if (c[i] == 'I') {
				ans += 2 * X1 - n;
				X++;
				X1 = upper_bound(x + 1, x + n + 1, X) - (x + 1);
				X2 = lower_bound(x + 1, x + n + 1, X) - (x + 1);
			}
			if (c[i] == 'Z') {
				ans += n - 2 * X2;
				X--;
				X1 = upper_bound(x + 1, x + n + 1, X) - (x + 1);
				X2 = lower_bound(x + 1, x + n + 1, X) - (x + 1);
			}
			printf("%lld\n", ans);
		}
	}
}
int main() {
	cyxyc::solve();
	return 0;
}