概率和期望

概率

基本定义

• 随机事件：某种现象在个别实验中其结果呈现出不确定性，而在大量重复实验中其结果又具有统计规律性。

• 随机试验 的特点：

  1. 可以在 相同条件 下重复进行；
  2. 每次实验的可能结果可以不止一个，并且 事先能明确实验的所有可能结果；
  3. 进行一次试验之前不能确定那个结果会出现。

• 样本空间：某个随机事件 所有可能的结果 的集合，一般记为 \(S\)。一般都假设 \(S\) 由有限个元素组成。

• 样本点：每个实验结果，即样本空间的元素。

• 随机事件：样本空间的子集，可简称为 事件。

• 事件 发生：当且仅当这一子集中的一个样本点出现时。

• 基本事件：由 一个样本点组成的单个元素的集合。

• 必然事件：在某种条件下，一定会发生的事件，称为 相对于该条件 的必然事件，简称必然事件。

• 不可能事件：在某种条件下，一定不会发生的事件，称为 相对于该条件 的不可能事件，简称不可能事件。

• 随机事件：在某种条件下，可能发生、也可能不发生的事件，叫做 相对于该条件 的随机事件，简称随机事件。

名称	定义	符号表达
包含关系	如果事件 A 发生，则时间 B 一定发生，这时称时间 B 包含事件 A；也可称为事件 A 包含于事件 B	\(B \supseteq A, A \subseteq B\)
相等关系	若 \(B \supseteq A\) 且 \(B \subseteq A\)，那么称事件 A 和事件 B 相等	\(A = B\)
并事件	若事件 C 发生当且仅当事件 A 发生或事件 B 发生，则称事件 C 为事件 A 与事件 B 的并事件，或称为和事件	\(A \cup B, A + B\)
交事件	若事件 C 发生当且仅当事件 A 发生且事件 B 发生，则称事件 C 为事件 A 和事件 B 的交事件，或称为积事件	\(A \cap B, A \times B\)
互斥事件	若 \(A \cap B\) 为不可能事件，也就是事件 A 和事件 B 不可能同时发生，则称事件 A 与事件 B 互斥或互不相容	\(A \cap B = \varnothing\)
对立事件	若 \(A \cap B\) 为不可能事件，且 \(A \cup B\) 为必然事件，那么称事件 A 与事件 B 互为对立事件	\(A \cap B = \varnothing, P(A \cup B) = P(A) + P(B) = 1\)

• 事件：随机事件 和 确定事件（必然事件 + 不可能事件）。

• 频数：在 相同条件下 重复进行 \(n\) 次实验，观察事件 A 是否发生，称事件 A 在 \(n\) 次实验中出现的次数 \(n_A\) 为事件 A 的频数。

• 频率：事件 A 出现的比例 \(f_n(A) = \frac{n_A}{n}\) 为事件 A 的频率。

• 概率：对于给定的随机事件 A，由于事件 A 发生的频率 \(f_n(A)\) 随着试验次数的增加基本稳定于某个常数上，把整个常数记为 \(P(A)\)，称为事件 A 的概率。

• \(n\) 重伯努利试验（重复 \(n\) 次）：一次实验中事件 A 发生的概率为 \(p\)，那么重复 \(n\) 次独立实验中这个时间恰好发生 \(k\) 次的概率为

\[P_n(k) = C_n^k \times p^k \times (1 - p)^{n - k} \]

• 概率的意义：

  1. 随机事件在一次的实验中是否发生是随机的，但随机性中含有规律性；
  2. 概率是频率的稳定值，概率大小，并不代表事件一定是否发生。

• 概率的性质：

  1. 非负性：对于任意一个事件 A，\(0 \le P(A) \le 1\)；
  2. 规范性：对于必然事件 A，\(P(A) = 1\)，对于不可能事件 B，\(P(B) = 0\)；
  3. 可加性：对于 \(n\) 个 互斥事件，\(p(A_1 \cup A_2 \cup A_3 \cup \cdots \cup A_n) = P(A_1) + P(A_2) + P(A_3) + \cdots + P(A_n)\)；
  4. 可乘性：对于 \(n\) 个 独立事件，\(P(A_1 \cap A_2 \cap A_3 \cap \cdots \cap A_n) = P(A_1) + P(A_2) + P(A_3) + \cdots + P(A_n)\)。

例题

Description

xyc 写了三套高考真卷，但由于分心想了 xy，所以无法保证三套真卷都能得满分。但是由于他真的想和 xy 聊会儿天，于是他拜托你求出以下概率：

1. 只有第一套真卷满分；
2. 只有一套真卷满分；
3. 第一套真卷满分，后面两套真卷至少有一个不是满分；
4. 三套真卷最多有两套满分；
5. 三套真卷都不是满分。

Train of Thought

这里我们用 \(A_i\) 表示第 \(i\) 套真卷满分，\(\overline{A_i}\) 表示第 \(i\) 套真卷不是满分。

1. \(P_1 = A_1 \overline{A_2} \ \overline{A_3}\)；
2. \(P_2 = A_1 \overline{A_2} \ \overline{A_3} \cup \overline{A_1} A_2 \overline{A_3} \cup \overline{A_1} \ \overline{A_2} A_3\)；
3. \(P_3 = A_1(\overline{A_2} \cup \overline{A_3})\)；
4. \(P_4 = \overline{A_1A_2A_3}\)，也可以表示为 \(P_4 = \overline{A_1} \cup \overline{A_2} \cup \overline{A_3}\)；
5. \(P_5= \overline{A_1} \ \overline{A_2} \ \overline{A_3}\)，也可以表示为 \(P_5 = \overline{A_1 \cup A_2 \cup A_3}\)。

注

根据知乎用户文章内容，取反应当使用 \bar，但由于显示问题（\bar 只有一条非常短的直线），故这里使用 \overline 代替。

以下为显示效果：

• \bar：\(\bar{A_i}, \bar{A_1A_2A_3}\)
• \overline：\(\overline{A_i}, \overline{A_1A_2A_3}\)

古典概率

定义

• 古典概率：又称 事前概率，指当随机事件中的各种可能发生的结果及其出现的次数都可以由演绎或外推法得知，而无需经过任何统计实验即可计算各种可能发生结果的概率。

• 古典概型（等可能概型） 的特点：

  1. 实验的样本空间有限；
  2. 实验中每个结果出现的可能性相同（都为等可能事件）；
  3. 发生的事件互不相容。

• 古典定义：计算 古典概型概率 的方法，又称古典概率。

• 计算古典概率：在 全部可能出现 的基本事件范围内，构成事件 A 的基本事件有 \(a\) 个，不构成事件 A 的基本事件由 \(b\) 个，则事件 A 的概率为 \(P(A) = \frac{a}{a + b}\)。

公式 / 定理

类似容斥原理进行理解：

\[P(A \cup B) = P(A) + P(B) - P(A \cap B) \]

例题

Description

有 \(40\) 支圆珠笔，其中有 \(30\) 支黑笔，\(10\) 支红笔。从中任意取 \(4\) 支，求这 \(4\) 支笔中至少包含 \(1\) 支红笔的概率。

Train of Thought Ⅰ

设事件 A \(\sim\) D 分别表示取出的 \(4\) 支笔中由 \(1 \sim 4\) 支红笔的概率。

由定义易得：

\[P(A) = \frac{C_{10}^1 \times C_{30}^3}{C_{40}^4} = \frac{40600}{91390}; \]

\[P(B) = \frac{C_{10}^2 \times C_{30}^2}{C_{40}^4} = \frac{19575}{91390}; \]

\[P(C) = \frac{C_{10}^3 \times C_{30}^1}{C_{40}^4} = \frac{3600}{91390}; \]

\[P(D) = \frac{C_{10}^4}{C_{40}^4} = \frac{210}{91390}. \]

所以 \(P(A \cup B \cup C \cup D)= P(A) + P(B) + P(C) + P(D)= \frac{40600}{91390} + \frac{19575}{91390} + \frac{3600}{91390} + \frac{210}{91390}= \frac{63985}{91390} = \frac{12597}{18278}\)

Train of Thought Ⅱ

求出取出的 \(4\) 支笔中一支红笔也没有的情况，再用 \(1\) 将其减去。

可以表示为

\[P(\complement_\Omega A) = P(\Omega) - P(A) = 1 - \frac{27405}{91390} = \frac{63985}{91390} = \frac{12597}{18278} \]

条件概率

定义

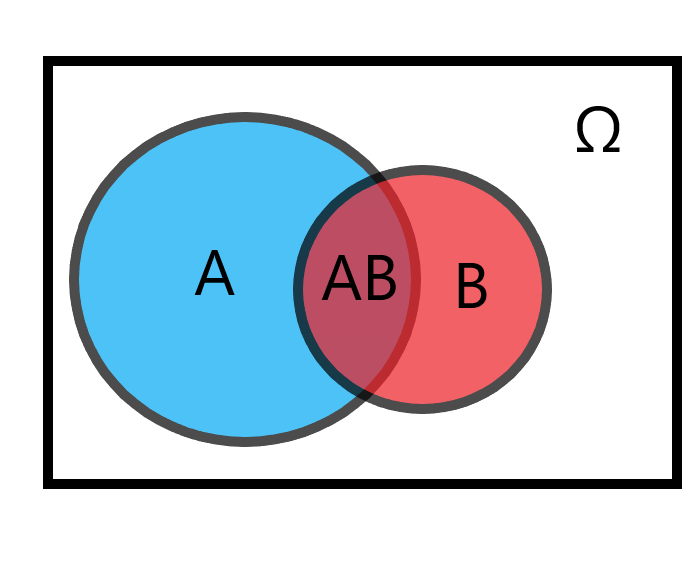
事件 A 和事件 B 不互相独立。计算在事件 A 已发生的前提下，事件 B 发生的概率，记作 \(P(B \mid A) = \frac{P(AB)}{P(A)}\)。

例题

Description Ⅰ

七年级四班有 \(45\) 名学生，这些学生中有男生、女生，不是还可以有别的吧，其中一些人是团员，人数见下：

	$\ \ \ \ \ \ $ 团员 $\ \ \ \ \ \ $	$\ \ \ \ \ \ $ 不是团员 $\ \ \ \ \ \ $	$\ \ \ \ \ \ $ 合计 $\ \ \ \ \ \ $
男生	16	9	25
女生	14	6	20
合计	30	15	45

现在班里需要选出一人制作表白墙（随机），班主任薛咩希望你告诉他选到男生的概率。

Train of Thought Ⅰ

设事件 A 表示选到男生。则可以表示为：

\[P(A) = \frac{n(A)}{n(\Omega)} = \frac{25}{45} = \frac{2}{9} \]

Description Ⅱ

随着随机选取后的一步步揭秘，现在已经知道选出来的是一个团员。现在薛咩希望知道，选到男生的概率是多少。

Train of Thought Ⅱ

设事件 B 表示选到团员，则可以表示为 \(P(A \mid B)\)。这时相当于以事件 B 为样本库考虑事件 A 发生的概率，此时的事件 A 就是积事件 AB，包含的样本点数为 \(n(AB) = 16\)。可得：

\[P(A \mid B) = \frac{n(AB)}{n(B)} = \frac{16}{30} = \frac{8}{15} \]

公式 / 定理

1. \[P(B \mid A) = \frac{n(AB)}{n(A)} \]

2. \[P(b \mid A) = \frac{P(AB)}{P(A)} \]

证明

\[P(B \mid A) = \frac{n(AB)}{n(A)} = \frac{\frac{n(AB)}{n(\Omega)}}{\frac{n(A)}{n(\Omega)}} = \frac{P(AB)}{P(A)} \]

例题

Description

“人文初”组有 \(3\) 男生和 \(2\) 个女生，现在每次随机选取一个人送去逝场参加考逝。远在天堂的 \(\textsf{scollop}\) 希望知道：

1. 第一次选到男生且第二次选到女生的概率；
2. 第一次已经选到男生，第二次选到女生的概率。

Train of Thought Ⅰ

设事件 A 为第一次抽到男生，事件 B 为第二次抽到女生。

第一问可以表示为求 \(P(AB)\)。

\[n(\Omega) = A_5^2 = 5 \times 4 = 20 \]

\[\because n(AB) = A_3^1 \times A_2^1 = 3 \times 2 = 6 \]

\[\therefore P(AB) = \frac{n(AB)}{n(\Omega)} = \frac{6}{20} = \frac{3}{10} \]

第二问可以表示为求 \(P(B \mid A)\)。

\[P(B \mid A) = \frac{P(AB)}{P(A)} = \frac{\frac{3}{10}}{\frac{3}{5}} = \frac{1}{2} \]

\[P(AB) = \frac{n(AB)}{n(\Omega)} = \frac{6}{20} = \frac{3}{10} \]

Train of Thought Ⅱ

\[\because n(A) = 3 \times 4 = 12, n(AB) = 3 \times 2 = 6 \]

\[\therefore P(B \mid A) = \frac{n(AB)}{n(A)} = \frac{6}{12} = \frac{1}{2} \]

\[\because P(A) = \frac{3}{5} \]

\[P(AB) = P(A)P(B \mid A) = \frac{3}{5} \times \frac{1}{2} = \frac{3}{10} \]

公式 / 定理

设 \(P(A) > 0\)，有：

1. \(P(\Omega \mid A) = 1\)；
2. \(\textrm{if }B \cap C = \varnothing, \textrm{then }P(B \cup C \mid A) = P(B \mid A) + P(C \mid A)\)；
3. \(\textrm{if }A \cap B = \varnothing, P(A \cup B) = 1, \textrm{then }P(\overline{B} \mid A) = 1 - P(B \mid A)\)。

公式 / 定理

• 乘法公式：\(P(AB) = P(B \mid A) \times P(A) = P(A \mid B) \times P(B)\)
• 全概率公式：设 \(A_1, A_2, A_3, \cdots, A_n\) 是一组两两互斥的事件（即不可能同时发生），\(A_1 \cup A_2 \cup A_3 \cup \cdots \cup A_n = \Omega\)，且 \(\forall{i \in{[1, n]}}: P(A_i) > 0\)，有

\[\forall{B \subseteq{\Omega}}: \sum_{i = 1}^{n} A_i = 1 \]

\[\forall{B \subseteq{\Omega}}: P(B) = \sum_{i = 1}^{n}P(A_i)P(B \mid A_i) \]

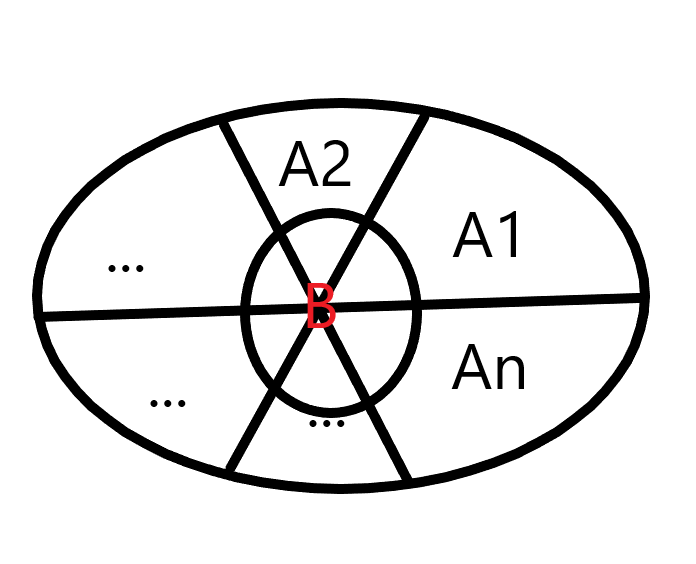
• 贝叶斯定理：设 \(A_1, A_2, A_3, \cdots, A_n\) 是一组两两互斥的事件，\(A_1 \cup A_2 \cup A_3 \cup \cdots \cup A_n = \Omega\)，且 \(\forall{i \in{[1, n]}}: P(A_i) > 0\)，有

\[\forall{i \in{[1, n]}, B \subseteq{\Omega}, P(B) > 0}: P(A_i \mid B) = \frac{P(BA_i)}{P(B)} = \frac{P(A_i)P(B \mid A_i)}{P(B)} = \frac{P(A_i)P(B \mid A_i)}{\sum_{n}^{j = 1}P(A_j)P(B \mid A_j)} \]

例题

Description

在一个柜子里有一堆真卷，其中 \(50\%\)、\(30\%\)、\(20\%\) 分别是 xyc、wdz、hyf 写的，且三人的作业的满分率分别是 \(\frac{1}{10}\)、\(\frac{1}{15}\)、\(\frac{1}{20}\)，现在在这堆作业中任取一件，求取出的不是满分试卷的概率是多少。

Train of Thought

设事件 \(A_1\)、\(A_2\)、\(A_3\) 表示取出的试卷分别是 xyc、wdz、hyf 的试卷，设事件 B 表示取出的试卷不是满分。可得：

\[P(A_1) = \frac{9}{10}, P(A_2) = \frac{3}{10}, P(A_3) = \frac{2}{10} \]

\[P(B \mid A_1) = \frac{9}{10}, P(B \mid A_2) = \frac{14}{15}, P(B \mid A_3) = \frac{19}{20} \]

由全概率公式，得：
\(P(B)= P(B \mid A_1)P(A_1) + P(B \mid A_2)P(A_2) + P(B \mid A_3)P(A_3)= \frac{9}{10} \times \frac{9}{10} + \frac{14}{15} \times \frac{3}{10} + \frac{19}{20} \times \frac{2}{10} = \frac{23}{25}\)

Description

有三个题单，第一个题单有 \(3\) 道黑题和 \(1\) 道紫题，第二个题单有 \(2\) 道黑题和 \(3\) 道紫题，第三个题单有 \(3\) 道黑题和 \(2\) 道紫题（三个题单中没有重复的题），准备内卷的 Ri 希望知道：

1. 随机选取一个题单，再从这个题单里随机选一道题，这道题是紫题的概率；
2. 若选到的是紫题，这道题属于第三个题单的概率。

Train of Thought

设事件 A 为选到紫题，事件 B\(_ i, i \in{[1, 3]}\) 表示选到第 \(1, 2, 3\) 个题单。

1. \(P(A) = \sum_{i = 1}^{3}P(B_i)P(A \mid B_i)\)

   \(P(A) = \frac{1}{3} \times (\frac{1}{4} + \frac{2}{5} + \frac{3}{5}) = \frac{5}{12}\)

2. \(P(B_3 \mid A) = \frac{P(AB_3)}{P(A)} = \frac{P(B_3)P(A \mid B_3)}{P(A)} = \frac{\frac{1}{3} \times \frac{2}{5}}{\frac{5}{12}} = \frac{8}{25}\)

概率 DP

包括 DP 求概率 和 DP 求期望（亦称期望 DP）。这里先写 DP 求概率。

这类题目采用顺推，也就是从初始状态推向结果。同一般的 DP 类似的，难点依然是对状态转移方程的刻画，只是这类题目经过了概率论知识的包装。
——OI Wiki

概率 DP 通常是已知初始状态，然后求达到目标的概率，转移方程为 \(f_i = f_{i - 1} \times p_i\)。

例题

1. CF148D Bag of mice
   link for Codeforces: here
2. POJ3071 Football
3. CF768D Jon and Orbs
   link for Codeforces: here
4. LightOJ Just another Robbery
5. CF248E Piglet's Birthday
   link for Codeforces: here

期望

基本定义

• 离散型随机变量：在一定空间内变量取值为有限个，或数值可以一一枚举出来的变量。

在信竞中的期望值问题，大多数都是求离散型变量的数学期望。

• 数学期望：对于一个离散化随机变量，其数学期望 \(=\) 实验中每次可能的结果 \(\times\) 其结果概率的总和。

设离散型随机变量 \(X\) 的概率分布为 \(p_i = P\{ X = x_i \}\)，若和式 \(\sum x_i p_i\) 绝对收敛，则称其值为 \(X\) 的 期望，记作 \(EX\)。
——OI Wiki

表示

• \(E(x)\)：事件 A 有很多种，其结果的大小为 \(x\)，那么 \(x\) 的期望值表示事件 A 的结果的平均大小。

• \(E(x)=\) 每种结果的大小与其概率的乘积的和。表示为：

\[E(x) = \sum_{i = 1}^{n} p_i \times x_i \]

\(x_i\) 表示离散的随机变量 \(X\) 的输出值，\(p_i\) 表示输出值对应的概率。

性质

线性性

若随机变量 \(X, Y\) 的期望存在，则有：

• 对于任意实数 \(a, b\)，\(E(aX + bY) = a \times E(X) + b \times E(Y)\)
• \(E(X + Y) = E(X) + E(Y)\)

随机变量乘积的期望

若随机变量 \(X, Y\) 的期望存在且 \(X, Y\) 相互独立，则有：

\[E(XY) = E(X) \times E(Y) \]

注意：上述性质中的“独立性” 并非 必要条件。
counterexample：考察随机变量 \(X\) 和 \(Y\)，其中 \(X\) 服从 \([-1, 1]\) 上的均匀分布，\(Y = X^2\)。

期望和概率的转换

This part is from OI Wiki.

对于随机事件 \(A\)，考虑其示性函数 \(I_A\)：

\(I_A(\omega) = \begin{cases} 1, & \omega \in A \\ 0, & \omega \notin A \end{cases}\)

根据定义可以求得其期望 \(EI_A = P(A)\)。这一转化在实际应用中非常常见。

条件分布与条件期望

link.

全期望公式

\(E[E[X|Y]] = E(X)\)

期望 DP

常用方法

1. 设 \(f_i\) 表示的是由 \(i\) 状态变成最终状态的期望（逆推）；
2. 按照题意直接设；
3. 把选择的东西加入数组。

求转移方程

大多数期望 DP 需要逆推（也不乏少数正推的）。

当求解到某一目标的期望花费时，由于最终的花费无从知晓（无法从无穷推起），因此期望 DO 需要倒叙求解。

设 \(f_i\) 为 \(i\) 状态下实现目标的期望值，即到了 \(f_i\) 这个状态的差距是多少。

初始时，将 \(f_n\) 初始化为 \(0\)，即在目标状态期望值为 \(0\)，然后进行状态转移，转移过程为 \(f_{i - 1} = f_i \times p_i + w\)，最终 \(f_0\) 即为所求。

当转移关系不成环时，期望 DP 可以进行线性递推；当转移关系成环时，期望 DP 的最终状态相当于一个已知量，转移关系相当于一个个方程，此时需要使用高斯消元法解决。

例题

1. POJ2096 Collecting Bugs
2. HUD2853 LOOPS
3. P4316 绿豆蛙的归宿
4. P1365 WJMZBMR打osu! / Easy
5. P3232 [HNOI2013] 游走
6. LighrOJ Discovering Gold
7. LightOJ Dice (III)
8. CF235B Let's Play Osu!
   link for Codeforces: here
9. HDU6595 Everything Is Generated In Equal Probability
10. HDU6656 Kejin Player

参考

OI-Wiki:

• 概率论 基本概念
• 概率论 随机变量
• 概率论 随机变量的数字特征

CSDN: 动态规划 —— 概率 DP 与期望 DP

老师课件