字符串:匹配,Hash,KMP,Trie
前置芝士之定义
定义
字符串,就是由字符连接而成的序列。
——鲁迅
字符集
一个字符集 \(\Sigma\) 是一个建立了全序关系的集合。对于 \(\Sigma\) 中的任意两个不同的元素 \(\alpha\) 和 \(\beta\) 都可以比较大小,即只有 \(\alpha > \beta\) 或 \(\alpha < \beta\) 两种情况。
字符
字符集 \(\Sigma\) 中的元素被称为字符。
字符串
一个字符串 \(S\) 是将 \(n\) 个字符顺次排序形成的序列, \(n\) 被称为 \(S\) 的长度,表示为 \(|S|\)。
子串
字符串 \(S\) 的字串 \(S_{i \sim j}\),表示 \(S\) 串中从 \(i\) 到 \(j\) 的一段。即由 \(S_i,S_{i + 1},S_{i + 2},\cdots,S_{j - 2},S_{j - 1},S_{j}\) 组成的字符串。
有时用 \(S_{i \sim j}(i > j)\) 表示空串。
字串列
字符串 \(S\) 的子串列是从 \(S\) 中提取出若干元素组合为一个序列,且不改变这些元素的相对位置。对于一个字符串 \(S\),它的子串列为 \(S_{p_1},S_{p_2},\cdots,S_{p_k}\),且保证 \(1 \le p_1 < p_2 < \cdots < p_k \le |S|\)。
前缀
前缀是指从 \(S_1\) 开始,到 \(S_i\) 结束的一个特殊字串。字符串 \(S\) 的以 \(i\) 结尾的前缀可以表示为 \(Prefix(S,i)\),即 \(Prefix(S,i)=S_{0 \sim i}\)。
真前缀
真前缀是指 \(S\) 除了 \(S_{|S|}\)以外的前缀。即 \(S\) 的前缀为 \(S_1,S_{1 \sim 2},S_{1 \sim 3},\cdots,S_{1 \sim |S|-1}\),而 \(S\) 的真前缀为 \(S_1,S_{1 \sim 2},S_{1 \sim 3},\cdots,S_{1 \sim |S|-2}\)。
后缀
前缀是指从 \(S_i\) 开始,到 \(S_{|S|}\) 结束的一个特殊字串。字符串 \(S\) 的以 \(i\) 开始的前缀可以表示为 \(Suffix(S,i)\),即 \(Suffix(S,i)=S_{i \sim |S|-1}\)。
真后缀
真后缀是指 \(S\) 除了 \(S_1\)以外的后缀。即 \(S\) 的后缀为 \(S_{|S|-1},S_{|S|-1 \sim |S|-2},S_{|S|-1 \sim |S|-3},\cdots,S_{|S|-11 \sim 0}\),而 \(S\) 的真后缀为 \(S_{|S|-1},S_{|S|-1 \sim |S|-2},S_{|S|-1 \sim |S|-3},\cdots,S_{|S|-1 \sim 1}\)。
字典序
以第 \(i\) 个字符作为第 \(i\) 关键字进行大小比较。
空字符小于字符集中任意字符。
回文串
回文串是指正着写和反着写完全相同的字符串,即满足 \(\forall 1 \le i \le |S|,S_i = S_{|S| + 1 - i}\) 的 \(S\)。
标准库
详见鲁迅。
字符串匹配
定义
又称模式匹配(\(\text{pattern matching}\))。该问题可以概括为给定字符串 \(S\) 和 \(T\),在主串 \(S\) 中寻找子串 \(T\)。字符 \(T\) 称为模式串 (\(\text{pattern}\))。
类型
- 单串匹配:给定一个模式串和一个待匹配串,找出前者在后者中的所有位置。
- 多串匹配:给定多个模式串和一个待匹配串,找出这些模式串在后者中的所有位置。
- 出现多个待匹配串时,将它们直接连起来便可作为一个待匹配串处理。
- 可以直接当做单串匹配,但是效率不够高。
- 其他类型:例如匹配一个串的任意后缀,匹配多个串的任意后缀……
解法
详见下文 \(\text{hash}\)。
\(\text{Hash}\)
对于字符串匹配问题,可以考虑 \(\text{Hash}\) 做更优、更有效的做法。
定义
\(\text{Hash}\) 是指把一个函数映射到整数的函数 \(f\),通过这个函数,可以更方便的比较两个字符串的大小。
思想
类似于进制转换。
举个栗子,\((110110) _ 2\) 转为十进制的具体过程为 \(1 \times 2^5 + 1 \times 2^4 + 0 \times 2^3 + 1 \times 2^2 + 1 \times 2^1 + 0 \times 2^0\),即按权展开。运用这样的思想,我们把每个字符视为 \(p\) 进制下的一个数,(例如每个数都视为自己的 \(\text{ASCII}\) 码;或把 \(a\) 视为 \(1\),\(b\) 视为 \(2\) 等),那么可以把一个字符串 \(abceda\) 表示为 \(1 \times p^5 + 2 \times p^4 + 3 \times p^3 + 5 \times p^2 + 4 \times p^1 + 1 \times p^0\)。当然,这样的数有可能会肥肠大,所以一般对这个数取模 \(q\)。
做法
单哈希
即取一个 \(p\) 和 \(q\),将每个字符串 \(S\) 表示为 \(hash = S_0 \times p^{|S| - 1} + S_1 \times p^{|S| - 2} + \dots + s_{|S|-1} \times p^0\)。这里求 \(\text{Hash}\) 时直接用了每个字符的 \(\text{ASCII}\) 值,当然,也可以将每个字符定义为其他数,看个人喜好。
由于
unsigned long long会将多余 \(2^{64}\) 的部分自动删除,即对 \(2^{64} - 1\) 取模,所以可以不取 \(q\)。即为自然溢出法。
双哈希
对于两个不相同的字符串,使用单哈希求出的值是可能相同的,所以可以引入;另一套 \(p,q\),使重复的概率降低,提升 \(\text{Hash}\) 的精度。
简单的,即将字符串 \(S\) 分别表示为 \(haah1 = S_0 \times p1^{|S| - 1} + S_1 \times p1^{|S| - 2} + \dots + s_{|S|-1} \times p1^0\) 和 \(hash2 = S_0 \times p2^{|S| - 1} + S_1 \times p2^{|S| - 2} + \dots + s_{|S|-1} \times p2^0\),则 \(S\) 的哈希值为 \(<hash1,hash2>\)。这样,两个字符串哈希值重复的概率就会大大降低。
公式
\(hash_i = hash_{i - 1} \times p + id_{s_i} \% q\),其中 \(id_i\) 表示字符 \(i\) 对应的值。
求字串的哈希值
使用 \(\text{Hash}\) ,可以用 \(O(1)\) 的时间复杂度求出字串的哈希值。
对于长度为 \(5\) 字符串 \(S\),已知
\(hash_1 = id_1;\)
\(hash_2 = id_1 \times p + id_2;\)
\(hash_3 = id_1 \times p^2 + id_1 \times p + id_3;\)
\(hash_4 = id_1 \times p^3 + id_2 \times p^2 + id_3 \times p + id_4;\)
\(hash_5 = id_1 \times p^4 + id_2 \times p^3 + id_3 \times p^2 + id_4 \times p + id_5;\)。
如果希望求出 \(S_{3 \sim 4}\),那么运用小学数学思维,可以用 \(hash_4 - hash_2 \times p^{4 - 3 + 1}\) 的方法,求出 \(id_3 \times p + id_4\),即 \(S_{3 \sim 4}\) 的哈希值。
公式
求字串 \(S_{l \sim r}\) 的哈希值,\(Hash = hash_r - hash_r \times p^{r - l + 1}\)。
如果考虑取模,那么应为 \(Hash = ((hash_r - hash_r \times p^{r - l + 1}) \% q + q) \% q\)。
\(\text{KMP}\)
前置芝士之前缀函数
定义
对于一个字符串 \(S\),其前缀函数被定义为一个长度为 \(|S|\) 数组 \(\pi\)。对于 \(\pi_i\):
- 如果子串 \(S_{0 \dots i}\) 有一对相等的真前缀 \(S_{0 \dots k - 1}\) 与真后缀 \(S_{i - (k - 1) \dots i}\),那么 \(\pi_i\) 就是这个相等的真前缀(或真后缀,是相等的)的长度,即 \(\pi_i = k\);
- 如果有不只一组相等的真前后缀,那么 \(\pi_i\) 就是其中最长的那一对的长度;
- 如果没有相等的,那么 \(\pi_i = 0\)。
简单说,\(\pi_i\) 就是字串 \(S_{0 \dots i}\) 最长的且相等的真前缀和真后缀的长度。
即 \(\pi[i] = \max_{k = 0 \dots i}\{k: S[0 \dots k - 1] = S[i - (k - 1) \dots i]\}\)。
\(\pi_0 = 0\)。
计算前缀函数
这部分都是鲁迅说的。
朴素算法
过程
一个直接按照定义计算前缀函数的算法流程:
在一个循环中以 \(i = 1\to n - 1\) 的顺序计算前缀函数 \(\pi[i]\) 的值(\(\pi[0]\) 被赋值为 \(0\))。
为了计算当前的前缀函数值 \(\pi[i]\),我们令变量 \(j\) 从最大的真前缀长度 \(i\) 开始尝试。
如果当前长度下真前缀和真后缀相等,则此时长度为 \(\pi[i]\),否则令 \(j\) 自减 \(1\),继续匹配,直到 \(j=0\)。
如果 \(j = 0\) 并且仍没有任何一次匹配,则置 \(\pi[i] = 0\) 并移至下一个下标 \(i + 1\)。
实现
vector<int> prefix_function(string s) {
int n = (int)s.length();
vector<int> pi(n);
for (int i = 1; i < n; i++)
for (int j = i; j >= 0; j--)
if (s.substr(0, j) == s.substr(i - j + 1, j)) {
pi[i] = j;
break;
}
return pi;
}
string substr (size_t pos = 0, size_t len = npos) const;
显见该算法的时间复杂度为 \(O(n^3)\),具有很大的改进空间。
第一个优化
第一个重要的观察是,相邻的前缀函数值至多增加 \(1\)。
参照下图所示,只需如此考虑:当取一个尽可能大的 \(\pi[i+1]\) 时,必然要求新增的 \(S[i+1]\) 也与之对应的字符匹配,即 \(S[i+1]=S[\pi[i]]\),此时 \(\pi[i+1] = \pi[i]+1\)。
\(\underbrace{\overbrace{S _ 0 ~ S _ 1 ~ S _ 2}^{\pi[i] = 3} ~ S _ 3} _ {\pi[i+1] = 4} ~ \dots ~ \underbrace{\overbrace{S _ {i-2} ~ S_{i-1} ~ S_ {i}}^{\pi[i] = 3} ~ S _ {i+1}} _ {\pi[i+1] = 4}\)
所以当移动到下一个位置时,前缀函数的值要么增加一,要么维持不变,要么减少。
实现
vector<int> prefix_function(string s) {
int n = (int)s.length();
vector<int> pi(n);
for (int i = 1; i < n; i++)
for (int j = pi[i - 1] + 1; j >= 0; j--) // improved: j=i => j=pi[i-1]+1
if (s.substr(0, j) == s.substr(i - j + 1, j)) {
pi[i] = j;
break;
}
return pi;
}
在这个初步改进的算法中,在计算每个 \(\pi[i]\) 时,最好的情况是第一次字符串比较就完成了匹配,也就是说基础的字符串比较次数是 \(n-1\) 次。
而由于存在 \(j = pi[i-1]+1(pi[0]=0)\) 对于最大字符串比较次数的限制,可以看出每次只有在最好情况才会为字符串比较次数的上限积累 \(1\),而每次超过一次的字符串比较消耗的是之后次数的增长空间。
由此我们可以得出字符串比较次数最多的一种情况:至少 \(1\) 次字符串比较次数的消耗和最多 \(n-2\) 次比较次数的积累,此时字符串比较次数为 \(n-1 + n-2 = 2n-3\)。
可见经过此次优化,计算前缀函数只需要进行 \(O(n)\) 次字符串比较,总复杂度降为了 \(O(n^2)\)。
第二个优化
在第一个优化中,我们讨论了计算 \(\pi[i+1]\) 时的最好情况:\(S[i+1]=S[\pi[i]]\),此时 \(\pi[i+1] = \pi[i]+1\)。现在让我们沿着这个思路走得更远一点:讨论当 \(S[i+1] \neq S[\pi[i]]\) 时如何跳转。
失配时,我们希望找到对于子串 \(S[0\dots i]\),仅次于 \(\pi[i]\) 的第二长度 j,使得在位置 \(i\) 的前缀性质仍得以保持,也即 \(S[0 \dots j - 1] = S[i - j + 1 \dots i]\):
\(\overbrace{\underbrace{S_0 ~ S_1} _ j ~ S_2 ~ S_3}^{\pi[i]} ~ \dots ~ \overbrace{S_{i-3} ~ S_{i-2} ~ \underbrace{S_{i-1} ~ S_{i}} _ j}^{\pi[i]} ~ S_{i+1}\)
如果我们找到了这样的长度 \(j\),那么仅需要再次比较 \(S[i + 1]\) 和 \(S[j]\)。如果它们相等,那么就有 \(\pi[i + 1] = j + 1\)。否则,我们需要找到子串 \(S[0\dots i]\) 仅次于 j 的第二长度 \(j^{(2)}\),使得前缀性质得以保持,如此反复,直到 \(j = 0\)。如果 \(s[i + 1] \neq s[0]\),则 \(\pi[i + 1] = 0\)。
观察上图可以发现,因为 \(S[0\dots \pi[i]-1] = S[i-\pi[i]+1\dots i]\),所以对于 \(S[0\dots i]\) 的第二长度 \(j\),有这样的性质:
\(S[0 \dots j - 1] = S[i - j + 1 \dots i]= S[\pi[i]-j\dots \pi[i]-1]\)
也就是说 \(j\) 等价于子串 \(S[\pi[i]-1]\) 的前缀函数值,即 \(j=\pi[\pi[i]-1]\)。同理,次于 \(j\) 的第二长度等价于 \(S[j-1]\) 的前缀函数值,\(j^{(2)}=\pi[j-1]\)
显然我们可以得到一个关于 \(j\) 的状态转移方程:\(j^{(n)}=\pi[j^{(n-1)}-1], \ \ (j^{(n-1)}>0)\)
最终算法
所以最终我们可以构建一个不需要进行任何字符串比较,并且只进行 \(O(n)\) 次操作的算法。
而且该算法的实现出人意料的短且直观:
实现
vector<int> prefix_function(string s) {
int n = (int)s.length();
vector<int> pi(n);
for (int i = 1; i < n; i++) {
int j = pi[i - 1];
while (j > 0 && s[i] != s[j]) j = pi[j - 1];
if (s[i] == s[j]) j++;
pi[i] = j;
}
return pi;
}
这是一个在线算法,即其当数据到达时处理它——举例来说,你可以一个字符一个字符的读取字符串,立即处理它们以计算出每个字符的前缀函数值。该算法仍然需要存储字符串本身以及先前计算过的前缀函数值,但如果我们已经预先知道该字符串前缀函数的最大可能取值 \(M\),那么我们仅需要存储该字符串的前 \(M + 1\) 个字符以及对应的前缀函数值。
\(\text{KMP}\)
\(\text{KMP}\) 算法,由 \(\text{D.E.Knuth}\),\(\text{J.H.Morris}\)和\(\text{V.R.Pratt}\) 在 \(\text{1977}\) 年共同发布,简称 \(\text{KMP}\) 算法(全称 \(\text{Knuth-Morris-Pratt}\) 算法),常用于在一个文本串中查找模式串的字符串匹配算法。
在这一部分,我们定义 \(\operatorname{txt}\) 为文本串,长度为 \(m\);\(\operatorname{pat}\) 为模式串,长度为 \(n\)。
暴力算法
对于 \(\operatorname{txt}\) 和 \(\operatorname{pat}\),我们希望在 \(\operatorname{txt}\) 中查询 \(\operatorname{pat}\),那么可以放置两个指针 \(i\) 和 \(j\),分别枚举 \(\operatorname{txt}\) 和 \(\operatorname{pat}\) 查询的位置。
简单地模拟一下暴力算法的过程:
对于 \(\operatorname{txt}=\{\text{abababcabaa}\}\) 和 \(\operatorname{pat}=\{\text{ababcabaa}\}\) :
\(i\) 和 \(j\) 都从第一位开始枚举
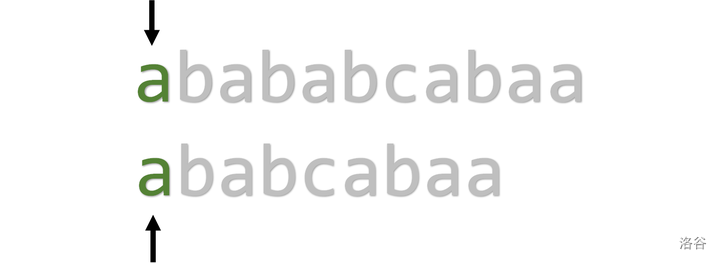
\(2 \sim 4\) 位依旧可以匹配,此时 \(i = 4, j = 4\)

当 \(i = 5, j = 5\) 时,\(\operatorname{txt} _ 5 = a, \operatorname{pat} _ 5 = c\),失配,指针回溯至 \(i = 2, j = 1\)

当 \(i = 2, j = 1\) 时, \(\operatorname{txt} _ 2 = b, \operatorname{pat} _ 2 = a\),失配,指针移至 \(i = 3, j = 1\)

当 \(i = 3, j = 1\) 时,可以匹配,直至结束,匹配成功
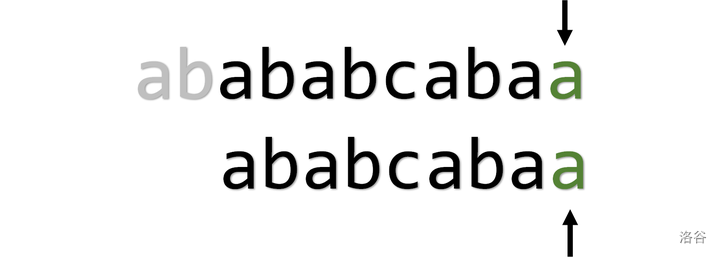
可以看到,暴力算法的时间复杂度为 \(O(mn)\),具体的,体现在每次失配后指针 \(i\) 都需要回溯,浪费了时间。但是如果 \(i\) 不回溯,只将 \(j\) 回溯至 \(1\),又会出现问题,如下:
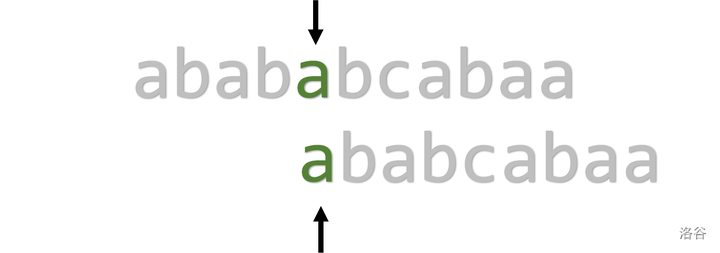
\(\text{KMP}\)
所以,问题体现在有没有方法不回溯 \(i\) 且不会出现漏洞呢?引用一张 \(\text{PMT}\)(\(\text{Partial Match Table}\),部分匹配表)。

可以看得出,\(j\) 应该赋值为多少,其实本质上只与 \(\operatorname{pat}\) 有关。具体的,即只需要找到 \(\operatorname{pat}\) 的前缀函数即可。
那么我们需要的,就是将 \(j\) 回溯到前缀函数处即可。
所以其实前缀函数不是前置芝士,而是 \(\text{KMP}\) 是前缀函数的一个最常见的应用。
前缀函数
所以 \(\text{KMP}\) 的具体思路就是:
- 指针 \(i\) 和 \(j\) 都从头开始枚举
2.1. 如果 \(\operatorname{txt} _ i == \operatorname{pat} _ j\),继续枚举
2.2. 如果 \(\operatorname{txt} _ i != \operatorname{pat} _ j\),指针 \(i\) 不动,\(j\) 回溯至 \(1\)
当然,这就需要你完全理解了前缀函数。关于前缀函数的 \(\text{KMP}\) 求法,去找鲁迅。(因为我不会(没看懂,连前缀函数的求法都没看懂))
实现
vector<int> find_occurrences(string text, string pattern) {
string cur = pattern + '#' + text;
int sz1 = text.size(), sz2 = pattern.size();
vector<int> v;
vector<int> lps = prefix_function(cur);
for (int i = sz2 + 1; i <= sz1 + sz2; i++) {
if (lps[i] == sz2) v.push_back(i - 2 * sz2);
}
return v;
}
\(\text{PMT}\)
其实,还可以通过刚刚提到的 \(\text{PMT}\) 来解决。
首先,需要明确一个概念,就是 \(\text{PMT}\) 的定义与前缀函数基本相同,都是求真前后缀(那有没有一种可能,这两个其实只是不同的说法呢)。
那么我看懂了的 \(\text{PMT}\) 是怎么回事呢?回顾暴力匹配第一次失败的情景

此时 \(\operatorname{txt} _ 5 = a\) 和 \(\operatorname{pat} _ 5 = c\) 没有匹配上,\(\text{KMP}\) 的想法是让指针 \(i\) 不回溯,所以这里不同于暴力,我们保持 \(i\) 不动,将 \(j\) 回溯。观察已经匹配成功的部分:\(abab\),为了尽可能节约时间复杂度,那么我们其实可以将前缀 \(ab\) 直接置于后缀 \(ab\) 处,即直接将 \(j\) 赋值为 \(3\)。其实也就是相同的、最长的真前、后缀。
前缀函数:亻尔女子
即如下图

实际上就是 j = pmt[j-1]。
再如下图
直接 j = pmt[j-1](\(j = 3\))
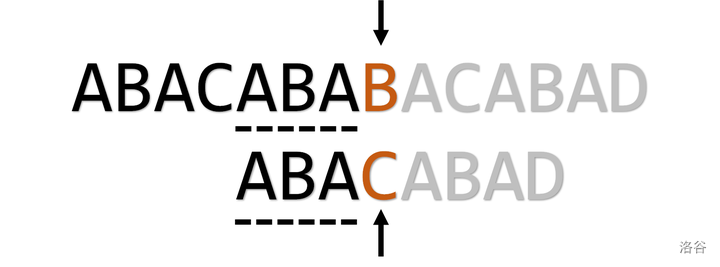
此时依旧不匹配

j = pmt[j-1](\(j = 2\))
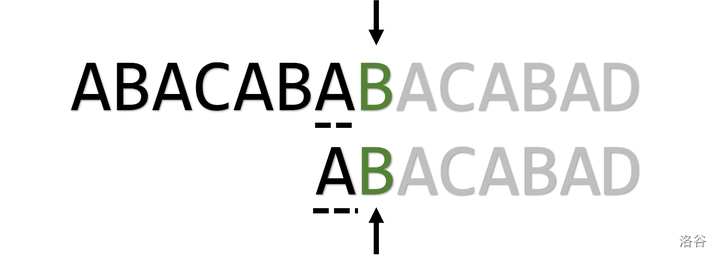
实现
for (int i = 1, j = 0; i < plen; i++) {
while (j && p[i] != p[j]) j = pmt[j - 1];
if (p[i] == p[j]) j++;
pmt[i] = j;
}
时间复杂度:\(O(n + m)\)。
优化
其实上述的过程/思路只能称为 \(\text{MP}\) 算法,\(\text{KMP}\) 中由 \(\text{Knuth}\) 提出的一部分包括一个常数优化。
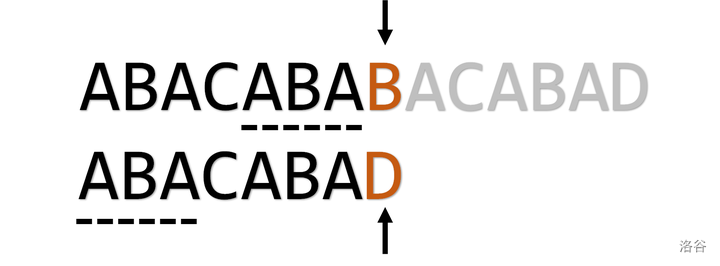
如下图,当我们试图匹配 \(abababd\) 和 \(abababc\) 时,就会发现,其实我们进行了几次无效的匹配。
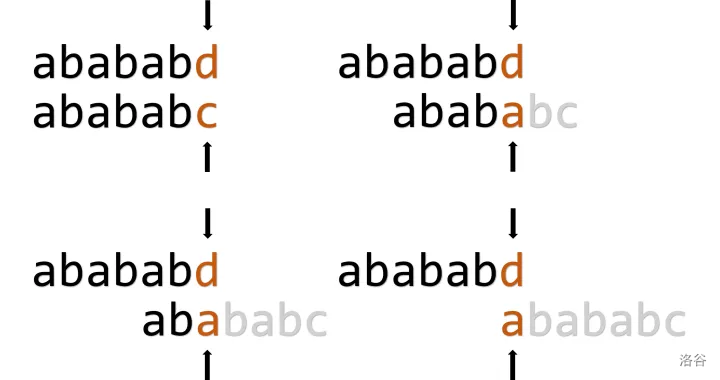
如果手推的话,明显看得出,\(d\) 是不可能匹配的了 \(c\) 的,但是只有上面的思路的话,代码中是无法做出这样的优化的。为了减少在这些无意义匹配上浪费的时间,可以在计算 \(\operatorname{pmt}\) 时,进行一些小改动。
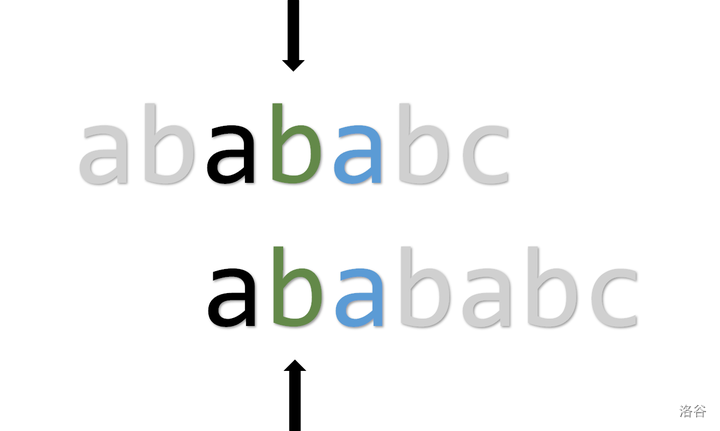
当出现上图情况时,按照原来的做法,应将 pmt[i] = ++j(\(pmt_i = 2\))。但是可以看出,\(p_{i + 1}\) 与 \(p_{j + 1}\) 是相同的,也就是说,假如 \(j = 4\) 时失配,那么 \(j = 2\) 时一定也会失配,所以就可以将路径压缩:pmt[i] = pmt[j](\(pmt_i = pmt_{2 - 1}\)),就可以实现直接跳过 \(j = 2\) 的情况了。即当 \(p_i = p_j\) 且 \(p_{i + 1} = p_{j + 1}\) 时,直接 pmt[i] = pmt[j],剩余情况则不变。
实现
void get_pmt(const string& p) {
for (int i = 1, j = 0; i < p.length(); i++) {
while (j && s[i] != s[j]) j = pmt[j - 1];
bool b = p[i] == p[j], c = p[i + 1] == p[j + 1];
if (b) pmt[i] = pmt[j++];
if (!b || !c) pmt[i] = j;
}
}
时间复杂度:\(O(n + m)\)。
对于循环中的
i++和j++,都会进行 \(n + m\) 次(没有优化)。虽然 \(j\) 在实际情况中可能不会到达 \(n + m\),但即使经过优化,由于 \(j\) 在任何情况下都不会小于 \(-1\),所以 \(j\) 减少的次数也不会大于 \(n + m - 1\),所以时间复杂度都为 \(O(n + m)\)。
字典树
字典树,英文名 \(\text{trie}\)。顾名思义,就是一个像字典一样的树。
——鲁迅
定义
字典树(\(\text{trie}\) 树),又名前缀树、单词查找树、键树,是一种多叉树结构,用来存储和查询字符串。
特点
对于 \(\text{trie}\) 树,用一张图来理解会比较简单。
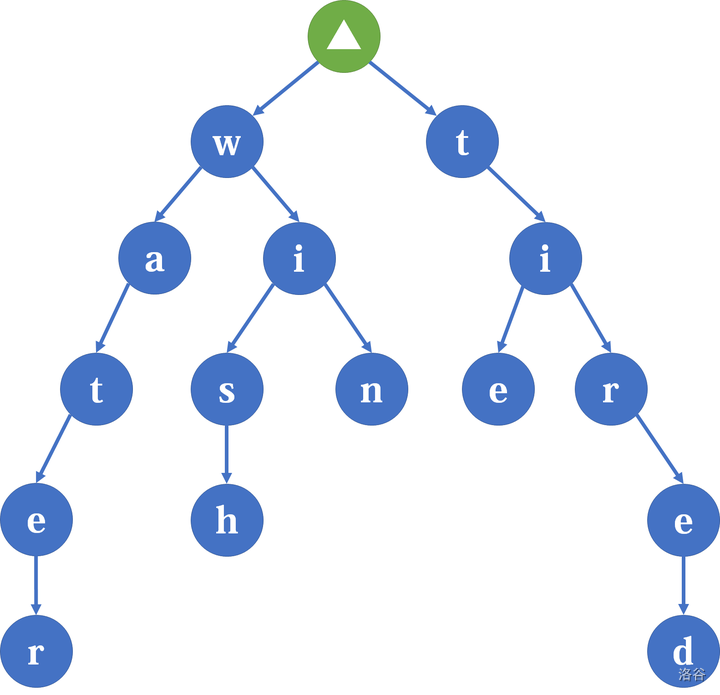
\(\text{trie}\) 树又名前缀树,所以对于图的观察也从前缀的角度看。那么,关键的字符集有:water,wish,win,tie,tired。
观察上图,可以得到一些性质(得不到就再画几张):
- 根节点不包括任何字符,除了根节点的每一个节点都包含且只包含一个字符;
- 从根节点开始到每一个节点,路径上所有节点的字符连接起来即为这个节点对应的字符串;
- 在同一个节点下的子节点包含的字符全部不相同(拥有相同前缀的字符串共用一个公共前缀)。
优/缺点
优点
- 有较高的插入、查询效率,时间复杂度为 \(O(len)\)(\(len\) 为字符串的长度);
对于查询时 \(\text{trie}\) 树和 \(\text{Hash}\) 的时间复杂度谁更优秀
可以知道,\(\text{Hash}\) 查询的时间复杂度为 \(O(1)\),但是对于 \(\text{Hash}\),其函数的优劣性决定了其效率、准确度,所以即使理论时间复杂度更优,效率也并不比 \(\text{trie}\) 树高太多。同时,在处理一些较短的字符串时,由于 \(\text{trie}\) 树不需要处理 \(\text{Hash}\) 值,因此拥有更优的时间复杂度。
- 在一般情况下,\(\text{trie}\) 树不同的关键字符不会产生冲突,只有在允许一个关键字符关联多个值时才会发生类似于 \(\text{Hash}\) 的冲突情况;
- 可以对关键字符按字典序排序,对于一些有需求的题可以起较好的作用。
缺点
- 对于一部分较好的 \(\text{Hash}\) 函数,\(\text{trie}\) 树在查询时的时间复杂度低于 \(\text{Hash}\);
- 由于 \(\text{trie}\) 树是一种空间换时间的数据结构,所以其空间复杂度较高。
实现
一般来说,我们会选择一种类似于链式前向星的写法来实现 \(\text{trie}\) 树。
const int N = 100005;
int nxt[N][26], cnt; //26取小写字母的数量,也可以改为其他
bool exist[N];
void init() {
memset(nxt, 0, sizeof(nxt));
cnt = 1;
}
void insert(char *s, int l) { //插入字符串
int cur = 1;
for (int i = 0; i < l; i++) { //尽可能使用以前已有的路径
if (!nxt[cur][s[i] - 'a']) nxt[cur][s[i] - 'a'] = ++cnt; //没有,添加新的节点
cur = nxt[cur][s[i] - 'a'];
}
exist[cur] = 1;
}
bool Find(char *s, int l) { //查找字符串
int cur = 1;
for (int i = 0; i < l; i++) {
if (!nxt[cur][s[i] - 'a']) return false;
cur = nxt[cur][s[i] - 'a'];
}
return exist[cur];
}
应用
检索字符串
检索是 \(\text{trie}\) 树最基本的应用,其思路就是按照前缀顺序搜索遍历。
- 若发现路径上的字符与文本字符不同,
return false; - 若全部比较结束后都相同,还需判断最后一个节点的标志位(判断该节点是否为一个关键字)。
标志位,设在节点结构,用于判断该节点能否构成一个单词(关键字)。
统计词频
即多次重复检索字符串的过程并统计次数。
\(\text{AC}\) 自动机
\(\text{trie}\) 树是 \(\text{AC}\) 自动机的一部分。
——鲁迅
前缀匹配
利用 \(\text{trie}\) 树使用公共前缀的特点,只需检索所有公共前缀 \(\text{txt}\),再统计其中标志位的数量即可。
\(\text{01-trie}\) 树
定义
将二进制数视为一个字符串,就可以建出一个字符集为 \(\{ 0,1 \}\) 的 \(\text{trie}\) 树。
维护异或极值
参考题目LuoguP4551 BZOJ1954 最长异或路径。
以下部分来自《狂树日记》:
BZOJ1954 最长异或路径
题意
给你一棵带边权的树,求 \((u, v)\) 使得 \(u\) 到 \(v\) 的路径上的边权异或和最大,输出这个最大值。
点数不超过 \(10^5\),边权在 \([0,2^{31})\) 内。
题解
随便指定一个根 \(root\),用 \(T(u, v)\) 表示 \(u\) 和 \(v\) 之间的路径的边权异或和,那么 \(T(u,v)=T(root, u)\oplus T(root,v)\),因为 \(LCA\) 以上的部分异或两次抵消了。
那么,如果将所有 \(T(root, u)\) 插入到一棵 \(trie\) 中,就可以对每个 \(T(root, u)\) 快速求出和它异或和最大的 \(T(root, v)\):
从 \(trie\) 的根开始,如果能向和 \(T(root, u)\) 的当前位不同的子树走,就向那边走,否则没有选择。
贪心的正确性:如果这么走,这一位为 1;如果不这么走,这一位就会为 0。而高位是需要优先尽量大的。
参考代码
维护异或和
\(\text{0-1 trie}\) 树支持修改、删除和全局加一。
\(\text{0-1 trie}\) 树的修改,其本质实际上为先进行删除操作,再进行重新插入。
而其的全局加一,也可以视为一种特殊的修改。
插入/删除
如果要维护异或和,我们只需要知道某一位上 \(0\) 和 \(1\) 个数的奇偶性即可,也就是对于数字 \(1\) 来说,当且仅当这一位上数字 \(1\) 的个数为奇数时,这一位上的数字才是 \(1\)。
维护异或和需要三个量:
ch[r][0/1]:表示节点 \(r\) 的两个子节点,ch[r][0]表示下一位为 \(0\),而ch[r][1]则表示下一位为 \(1\);w[r]:表示节点 \(r\) 到其父节点的这条边上数值的数量(权值),每插入一个数字 \(x\),\(x\) 二进制拆分后在 \(\text{trie}\) 上路径的权值就会+1;xorv[r]:表示以 \(r\) 为根节点的子树维护的异或和。
实现
void maintain(int o) {
w[o] = xorv[o] = 0;
if (ch[o][0]) {
w[o] += w[ch[o][0]];
xorv[o] ^= xorv[ch[o][0]] << 1;
}
if (ch[o][1]) {
w[o] += w[ch[o][1]];
xorv[o] ^= (xorv[ch[o][1]] << 1) | (w[ch[o][1]] & 1);
}
// w[o] = w[o] & 1;
// 只需知道奇偶性即可,不需要具体的值。当然这句话删掉也可以,因为上文就只利用了他的奇偶性。
}
- 这里的
MAXH指 \(trie\) 的深度,也就是强制让每一个叶子节点到根的距离为MAXH。对于一些比较小的值,可能有时候不需要建立这么深(例如:如果插入数字 \(4\),分解成二进制后为 \(100\),从根开始插入 \(001\) 这三位即可),但是我们强制插入MAXH位。这样做的目的是为了便于全局+1时处理进位。例如:如果原数字是 \(3(11)\),递增之后变成 \(4(100)\),如果当初插入 \(3\) 时只插入了 \(2\) 位,那这里的进位就没了。- 插入和删除,只需要修改叶子节点的
w[]即可,在回溯的过程中一路维护即可。
全局加一
顾名思义。即让\(\text{trie}\) 树中所有数值 +1。
实现
void addall(int o) {
swap(ch[o][0], ch[o][1]);
if (ch[o][0]) addall(ch[o][0]);
maintain(o);
}
合并
对于两个 \(\text{0-1 trie}\) 树,可以将其合并,同时合并维护的信息。
对于 \(\text{trie}\) 树的合并,可以考虑一个函数 int merge(int a, int b),其中 a、b 分别表示两棵 \(\text{trie}\) 树统一相对位置的节点编号。
合并时需要考虑三种情况:
a位置没有节点,return b;b位置没有节点,return a;a、b都存在,把b的信息合并到a上,然后递归处理a的左右儿子。
也可以选择新建一棵 \(\text{trie}\) 树,把两棵树的信息放入这棵新的树。
实现
int merge(int a, int b) {
if (!a) return b; // 如果 a 没有这个位置上的结点,返回 b
if (!b) return a; // 如果 b 没有这个位置上的结点,返回 a
/*
如果 `a`, `b` 都存在,
那就把 `b` 的信息合并到 `a` 上。
*/
w[a] = w[a] + w[b];
xorv[a] ^= xorv[b];
/* 不要使用 maintain(),
maintain() 是合并a的两个儿子的信息
而这里需要 a b 两个节点进行信息合并
*/
ch[a][0] = merge(ch[a][0], ch[b][0]);
ch[a][1] = merge(ch[a][1], ch[b][1]);
return a;
}
\(\text{trie}\) 树都可以合并,不限于 \(\text{0-1 trie}\) 树。
参考资料
前缀函数与 KMP 算法
算法学习笔记(13): KMP算法
KMP 算法详解(没怎么看)
字典树 (Trie)
Trie树(Prefix Tree)介绍
算法学习笔记(43): 字典树
Blog by cloud_eve is licensed under CC BY-NC-SA 4.0


 浙公网安备 33010602011771号
浙公网安备 33010602011771号