割点与桥(Tarjan)

\(\text{Tarjan}\) 求割点与桥

本来是打算总结 \(\text{Tarjan}\) 的，但是发现 \(\text{Tarjan}\) 涉及的部分过多，难以一次总结完，所以《暂时》分多篇博客分写，等什么时候基本都写完了再总结。~~反正是不可能学完的，flag 随便立。~~
贴一个网站，Tarjan（知乎版：Tarjan），讲得相当不错，如果想直接一口吞掉 \(\text{Tarjan}\) 算法的话可以看看。
Enjoy the blog.

定义

若果有志向看非常复杂详细定义的，这里——OI-Wiki。

注意：割点和桥只在无向图中讨论。

割点

对于一个无向图，如果把一个点删除后这个图的极大连通分量数增加了，那么这个点就是这个图的割点（又称割顶）。
——\(\text{OI-Wiki}\)

设 \(low_u\) 表示 \(u\) 所在子树中的节点经过至多一条非树边能到达的节点中最小的 \(\text{DFS}\) 序。实际上，这里只需要考虑反向边，很容易发现无向图是不存在横叉边的，前向边则对 \(low\) 没有影响。
如果 \(p\) 存在一个子结点 \(q\) 满足 \(low_q \ge dfn_p\) ，说明 \(q\) 无法通过它的子树“逃”到比 \(p\) 的 \(\text{DFS}\) 序更小的节点。那么，既然走子树走不通，\(q\) 如果想到达这样的点，只能选择经过它的父节点 \(p\)。因此，如果删去 \(p\)，\(q\) 和 \(\text{DFS}\) 序小于 \(p\) 点的点就分开了。
这时我们一般可以说 \(p\) 是割点了，只有一种特殊情况，就是 \(p\) 是 \(\text{DFS}\) 生成树的根节点的情形。这时，整个连通分量都不存在比 \(p\) 的 \(\text{DFS}\) 序更小的点。
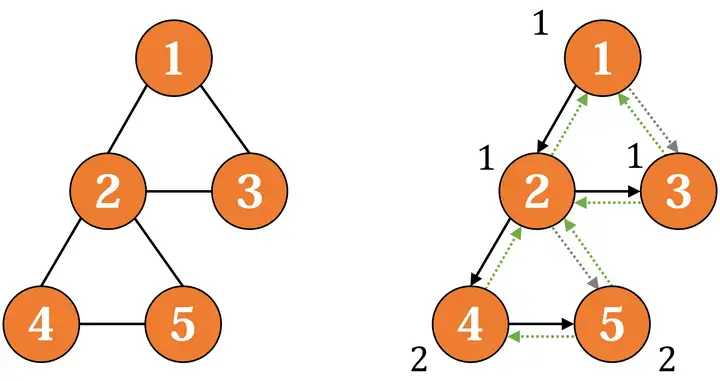
割点定义1
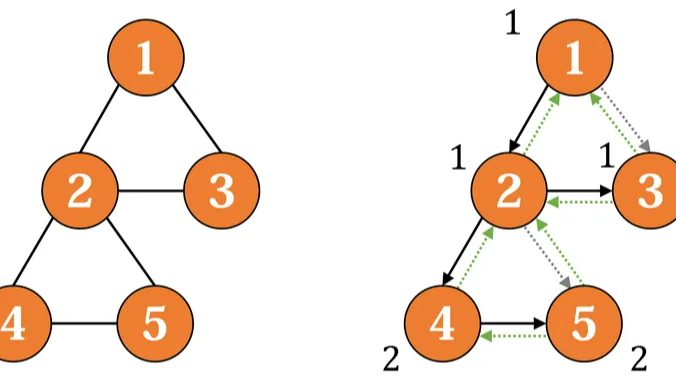
例如，上图中，\(2\) 号点是割点，但 \(1\) 号点不是，因为它是 \(\text{DFS}\) 生成树的根节点。这种特殊情况也很好处理：对于根节点，它如果有两个以上子节点，那么它就是割点。

显然删除根节点后这两个分支将会互不相连。

割点定义2
如图，就是一般情况，易得 \(2\) 号点是割点。

桥

和割点差不多的边，叫做桥。
对于一个无向图，如果删掉一条边后图中的连通分量数增加了，则称这条边为桥或者割边。严谨来说，就是：假设有连通图 \(G=\{V,E\}\)，\(e\) 是其中一条边（即 \(e \in E\)），如果 \(G-e\) 是不连通的，则边 \(e\) 是图 \(G\) 的一条割边（桥）。
——\(\text{OI-Wiki}\)

为了找到桥，我们要稍微修改一下 \(low\) 的定义：我们限定经过的那条非树边不能是从子节点直接到父节点的反向边。对于修改后的 \(low\)，我们可以断言：如果 \(q\) 是 \(p\) 的父节点，并且 \(low_q > dfn_p\)，那么 \(p \leftrightarrow q\) 是桥。
因为如果 \(p \leftrightarrow q\) 不是桥，那么删掉这条边后 \(q\) 一定有其他路径可以到达 \(p\)。注意无向图没有横叉边，想要到达 \(p\) 只能通过子树走反向边实现，那么 \(low_q \le dfs_n\) 应该成立，然而这与条件矛盾。因此 \(p \leftrightarrow q\) 正是桥。
桥定义1
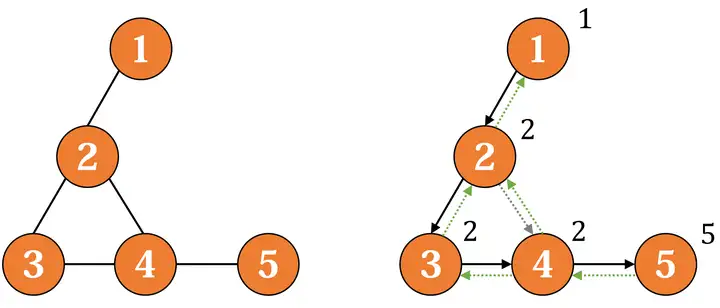
上图中 \(1 \leftrightarrow 2\) 和 \(4 \leftrightarrow 5\) 都是桥，如果不修改定义，将有 \(low_2 = 1\) 和 \(low_5 = 4\)，一座桥都找不到。
桥定义2
如图，易得 \(1 \leftrightarrow 2\) 是桥。

实现过程

割点

暴力算法

对于暴力算法：如果我们尝试删除每个点，并且判断这个图的连通性，那么复杂度会特别的高。
暴力法的原理就是通过定义求解割点和割边。在图中去掉某个顶点，然后进行 \(\text{DFS}\) 遍历，如果连通分量增加，那么该顶点就是割点。如果在图中去掉某条边，然后进行 \(\text{DFS}\) 遍历，如果连通分量增加，那么该边就是割边。对每个顶点或者每个边进行一次上述操作，就可以求出这个图的所有割点和割边，我们称之为这个图的割点集和割边集。

\(\text{Tarjan}\) 算法

相对于暴力，\(\text{Tarjan}\) 有更优的时间复杂度（\(\text{O(n+m)}\)）。
还是上文的图
割点过程1
首先，我们按照 \(\text{DFS}\) 序给他打上时间戳（访问的顺序）。
割点过程2
这些信息被我们保存在 \(dfn\) 数组中。
还需要另外一个数组 \(low\)，来存储不经过其父亲能到达的最小的时间戳。
例如 \(low_2\) 的话是 \(1\)，\(low_5\) 和 \(low_6\) 是 \(3\)。
然后我们开始 \(\text{DFS}\)，我们判断某个点是否是割点的根据是：对于某个顶点 \(u\)，如果存在至少一个顶点 \(v\)（\(u\) 的儿子），使得 \(low_v \ge dfn_u\)，即不能回到祖先，那么 \(u\) 点为割点。
此根据惟独不适用于搜索的起始点，其需要特殊考虑：若该点不是割点，则其他路径亦能到达全部结点，因此从起始点只「向下搜了一次」，即在搜索树内仅有一个子结点。如果在搜索树内有两个及以上的儿子，那么他一定是割点了（设想上图从 2 开始搜索，搜索树内应有两个子结点：\(3\) 或 \(4\) 及 \(5\) 或 \(6\)）。如果只有一个儿子，那么把它删掉，不会有任何的影响。比如下面这个图，此处形成了一个环。
割点过程3
我们在访问 \(1\) 的儿子时候，假设先 \(\text{DFS}\) 到了 \(2\)，然后标记用过，然后递归往下，来到了 \(4\)，\(4\) 又来到了 \(3\)，当递归回溯的时候，会发现 \(3\) 已经被访问过了，所以不是割点。

代码：

int dfs[MAXN], low[MAXN], cnt;
vector<int> cut; // 存储所有割点
void tarjan(int p, bool root = true) {
	int tot = 0;
	low[p] = dfs[p] = ++cnt;
	for (auto q : edges[p]) {
		if (!dfs[q]) {
			tarjan(q, false);
			low[p] = min(low[p], low[q]);
			tot += (low[q] >= dfs[p]); // 统计满足low[q] >= dfs[p]的子节点数目
		} else
			low[p] = min(low[p], dfs[q]);
	}
	if (tot > root) // 如果是根，tot需要大于1；否则只需大于0
		cut.push_back(p);
}

桥

暴力算法

免谈。大抵是 \(\textcolor{blue}{TLE}\) 的罢。

过程

和割点差不多，只要改一处：\(low_v>dfn_u\) 就可以了，而且不需要考虑根节点的问题。
割边是和是不是根节点没关系的，原来我们求割点的时候是指点 \(v\) 是不可能不经过父节点 \(u\) 为回到祖先节点（包括父节点），所以顶点 \(u\) 是割点。如果 \(low_v=dfn_u\) 表示还可以回到父节点，如果顶点 \(v\) 不能回到祖先也没有另外一条回到父亲的路，那么 \(u \leftrightarrow v\) 这条边就是割边。

代码

int low[MAXN], dfn[MAXN], dfs_clock;
bool isbridge[MAXN];
vector<int> G[MAXN];
int cnt_bridge;
int father[MAXN];

void tarjan(int u, int fa) {
	father[u] = fa;
	low[u] = dfn[u] = ++dfs_clock;
	for (int i = 0; i < G[u].size(); i++) {
		int v = G[u][i];
		if (!dfn[v]) {
			tarjan(v, u);
			low[u] = min(low[u], low[v]);
			if (low[v] > dfn[u]) {
				isbridge[v] = true;
				++cnt_bridge;
			}
		} else if (dfn[v] < dfn[u] && v != fa)
			low[u] = min(low[u], dfn[v]);
	}
}