强连通分量(Tarjan)

强联通分量与 $\text{Tarjan}$（求解）

定义

强连通分量$(\text{Strongly\ Connected\ Components,SCC})$的定义是：极大的强连通子图。
——$\text{OI-Wiki}$

所谓“极大的强连通子图”，就是说，在子图 $G'$（注意，强连通分量只针对有向图）上，所有点都可以通过边相连。如下图中，$1 \ 2 \ 4 \ 5 \ 6 \ 7 \ 8$ 构成的子图 $G'$ 即为子图 $G$ 的强连通分量。
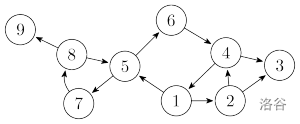
强连通分量-解释

对于点 $3$ 和 $9$：单独构成子图 $G$ 的强连通分量；强连通分量，包含所有边的连通子图才是子图 $G$ 的最大连通子图（强连通分量），这里的“极大”指的是点的数量。

在子图 $G$ 中，其强连通分量 $G'$ 可以缩为一个点，使子图 $G$ 变为一个有向无环图。一张图被称为有向无环图当且仅当此图不具有点集合数量大于一的强连通分量，因为有向环即是一个强连通分量，而且任何的强连通分量皆具有至少一个有向环。

处理

$\text{DFS}$ 生成树 是我们处理强连通分量最常用也是极好用的工具。
每当 $e$ 通过某条边访问到一个新节点 $v$，就加入这个点和这条边，最后得到的便是 $\text{DFS}$ 生成树。
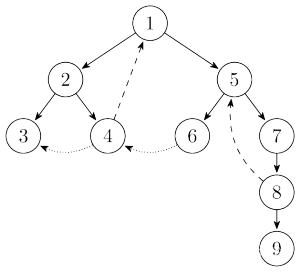
DFS生成树
有向图的 $\text{DFS}$ 生成树主要有 $4$ 种边：

树边（$\text{tree\ edge}$）：示意图中以实线边表示，每次搜索找到一个还没有访问过的结点的时候就形成了一条树边。
反祖边（$\text{back\ edge}$）：示意图中以长虚线边表示（即 $4 \rightarrow 1$），也被叫做回边、反向边，即指向祖先结点的边。
横叉边（$\text{cross\ edge}$）：示意图中以短虚线边表示（即 $4 \rightarrow 3$），它主要是在搜索的时候遇到了一个已经访问过的结点，但是这个结点 并不是 当前结点的祖先。
前向边（$\text{forward\ edge}$）：在图中没有示意（~~没想到吧~~），它是在搜索的时候遇到子树中的结点的时候形成的，容易知道移除前向边不会改变图的连通性，所以在讨论中基本忽略它。

还有一种边，是从一棵搜索树上的节点到另一棵搜索树上的节点的边，称为跨树边，但是跨树边在这里也发挥不了大的作用。
返祖边和横叉边都有一个特点：起点的 $\text{DFS}$ 序必然大于终点的 $\text{DFS}$ 序。
这可以导出一个有用的结论：对于每个强连通分量，存在一个点是其他所有点的祖先。若不然，则可以把强连通分量划成 $n$ 个分支，使各分支的祖先节点互相不为彼此的祖先。这些分支间不能通过树边相连，只能通过至少 $n$ 条横叉边相连，但这必然会违背上一段讲的性质。
DFS 根
（黑：树边$ ~~~~~~~ $绿：返祖边$ ~~~~~~~ $蓝：横向边）
我们把这个唯一的祖先节点称为强连通分量的根。显然，根是强连通分量中 $\text{DFS}$ 序最小的节点。

时间戳：$dfn_i$

在有向图的深度优先遍历中，记录每个点第一次被访问的时间的顺序，则这个顺序就是这个点的时间戳。在代码中我们用 $dfn_i$ 表示。每个点的时间戳不一定，取决于从哪个点开始遍历。时间戳可以帮我们判断这个点是否已经遍历过，有 $vis$ 的功能。

追溯值：$low_i$

在有向图中，点 $x$ 的追溯值为其子树满足一下条件的最小时间戳：

该点已经访问过，即有 $dfn$ 值；
存在一条从 $x$ 出发的边以它为终点。
也就是说，从一开始初始化时，在找回到走过的点之前，$low$ 值与 $dfn$ 值相同。

计算追溯值（寻找强连通分量的基本功）

初次访问点 $x$，入栈（为了后期更新追溯值，需要存储路径），并初始化为 $low_x = dfn _ x =++tot$；（栈可以用手写的，为 $stack_{++tot} = x$）
深度优先扫描点x连出去的边$(x,y)$；
开始判断：如果 $y$ 点访问过了，则 $low _ x = \min(low _ x ,dfn _ y )$，$y$ 是目前可追溯到的最早结点。如果 $y$ 没有访问过，那么继续遍历点 $y$，并设 $low _ x = low _ y$以便在后来的操作中找到了更早的追溯值来更新点 $x$ 的 $low$。
特判·点 $x$ 回溯前，判断是否有 $low _ x == dfn _ x$，有则说明点 $x$ 为一个强联通分量的头结点，这时我们就从 $x$ 的父节点开始弹出栈，直到 $x$ 出栈，而弹出的点就组成一个强连通分量。

$\text{Tarjan}$ 算法求强连通分量

在 $\text{Tarjan}$ 算法中为每个结点 $u$ 维护了以下几个变量：
一个栈：栈里的元素表示的是当前已经访问过但是没有被归类到任一强连通分量的结点。
$dfn _ u$：深度优先搜索遍历时结点 $u$ 被搜索的次序，即为时间戳（同上）。
$low _ u$：在 $u$ 的子树中能够回溯到的最早的已经在栈中的结点（实际操作中 $low _ i$ 不一定最小，但不会影响程序的最终结果）。设以 $u$ 为根的子树为 $Subtree _ u$。$low _ u$ 定义为以下结点的 $dfn$ 的最小值：$Subtree _ u$ 中的结点；从 $Subtree _ u$ 通过一条不在搜索树上的边能到达的结点。

另外一种关于 $low _ u$ 的表述：记录该点所在的强连通子图所在搜索子树的根节点的 $dfn$ 值。

一个结点的子树内结点的 $dfn$ 都大于该结点的 $dfn$。
从根开始的一条路径上的 $dfn$ 严格递增，$low$ 严格非降。

按照深度优先搜索算法搜索的次序对图中所有的结点进行搜索，维护每个结点的 $dfn$ 与 $low$ 变量，且让搜索到的结点入栈。每当找到一个强连通元素，就按照该元素包含结点数目让栈中元素出栈。在搜索过程中，对于结点 $u$ 和与其相邻的结点 $v$（$v$ 不是 $u$ 的父节点）考虑 $3$ 种情况：

$v$ 未被访问：继续对 $v$ 进行深度搜索。在回溯过程中，用 $low _ v$ 更新 $low _ u$。因为存在从 $u$ 到 $v$ 的直接路径，所以 $v$ 能够回溯到的已经在栈中的结点，$u$ 也一定能够回溯到。
$v$ 被访问过，已经在栈中：根据 $low$ 值的定义，用 $dfn _ v$ 更新 $low _ u$。
$v$ 被访问过，已不在栈中：说明 $v$ 已搜索完毕，其所在连通分量已被处理，所以不用对其做操作。

结点 $u$ 是某个强连通分量的根等价于 $dfn _ u$ 和 $low _ u$ 相等。简单可以理解成当它们相等的时候就不可能从 $u$ 通过子树再经过其它时间戳比它小的结点回到 $u$。

$dfn _ u == low _ u$，则 $u$ 是分量子树的树根。这是一个充要条件。
如果 $u$ 是树根，且由于是强分量，其子孙都可达到 $u$，则子孙的 $low$ 都是 $u$ 的编号。则 $low _ u = dfn _ u$。
如果 $low _ u == dfn _ u$，假设u不是树根，那么肯定有 $u$ 的祖先是树根，那么 $low _ u$ 肯定比当前值小。
$\therefore$ 矛盾，因此 $u$ 是树根。

伪代码参考

TARJAN_SEARCH(int u)
vis[u]=true
low[u]=dfn[u]=++dfncnt
push u to the stack
for each (u,v) then do
	if v hasn't been searched then
		TARJAN_SEARCH(v) // 搜索
		low[u]=min(low[u],low[v]) // 回溯
		else if v has been in the stack then
			low[u]=min(low[u],dfn[v])

对于一个连通分量图，我们很容易想到，在该连通图中有且仅有一个 $u$ 使得 $dfn _ u = low _ u$。该结点一定是在深度遍历的过程中，该连通分量中第一个被访问过的结点，因为它的 $dfn$ 和 $low$ 值最小，不会被该连通分量中的其他结点所影响。
因此，在回溯的过程中，判定 $dfn _ u = low _ u$ 是否成立，如果成立，则栈中 $u$ 及其上方的结点构成一个 $\text{SCC}$。

代码实现

int dfn[N], low[N], dfncnt, s[N], in_stack[N], tp;
int scc[N], sc;  // 结点 i 所在 SCC 的编号
int sz[N];       // 强连通 i 的大小

void tarjan(int u) {
	low[u] = dfn[u] = ++dfncnt, s[++tp] = u, in_stack[u] = 1;
	for (int i = h[u]; i; i = e[i].nex) {
		const int &v = e[i].t;
		if (!dfn[v]) {
			tarjan(v);
			low[u] = min(low[u], low[v]);
		} else if (in_stack[v]) {
			low[u] = min(low[u], dfn[v]);
		}
	}
	if (dfn[u] == low[u]) {
		++sc;
		while (s[tp] != u) {
			scc[s[tp]] = sc;
			sz[sc]++;
			in_stack[s[tp]] = 0;
			--tp;
		}
		scc[s[tp]] = sc;
		sz[sc]++;
		in_stack[s[tp]] = 0;
		--tp;
	}
}

时间复杂度：$O(n + m)$。

注意

$low _ u = \min(low _ u, dfn _ v)$ 当搜索到一条 $u \rightarrow v$ 的边，若 $v$ 仍在栈中，则 $v$ 必为 $u$ 的祖先，$u \rightarrow v$ 为一条后向边，由于形成后向边，则必构成环，该环中的所有点必为一个强联通分量或强连通分量中的某些点，对于后向边，我们需要对 $low$ 进行更新，因为 $low$ 记录的是能够追溯到的最早的栈中节点的次序号，所以 $low _ u = \min(low _ u, dfn _ v)$。
对于横跨边 $u \rightarrow v$，是不需要对 $low _ u$ 进行更新的。若一个节点已经访问过，则它的 $dfn$ 必有一个值，而当 $v$ 已经被访问过，但已经不在栈中（已经是一个强连通分量中的点），则 $u,v$ 不在同一 $\text{DFS}$ 上，此时构成了横跨边，没有祖先孙子关系，不需要对 $low$ 值进行更新。
回溯的时候，对树枝边的 $low _ u$ 就行更新，$Low _ u = \min(Low _ u, Low _ v)$。

$\text{Tarjan}$ 算法的操作原理

$\text{Tarjan}$ 算法基于定理：在任何深度优先搜索中，同一强连通分量内的所有顶点均在同一棵深度优先搜索树中。也就是说，强连通分量一定是有向图的某个深搜树子树。
可以证明，当一个点既是强连通子图 $G_1$ 中的点，又是强连通子图 $G_2$ 中的点，则它是强连通子图 $G_1 \cup G_2$ 中的点。
这样，我们用 $low$ 值记录该点所在强连通子图对应的搜索子树的根节点的 $dfn$ 值。注意，该子树中的元素在栈中一定是相邻的，且根节点在栈中一定位于所有子树元素的最下方。
强连通分量是由若干个环组成的。所以，当有环形成时（也就是搜索的下一个点已在栈中），我们将这一条路径的 $low$ 值统一，即这条路径上的点属于同一个强连通分量。
如果遍历完整个搜索树后某个点的 $dfn$ 值等于 $low$ 值，则它是该搜索子树的根。这时，它以上（包括它自己）一直到栈顶的所有元素组成一个强连通分量。

$\text{Tarjan}$ 算法的大致证明

在栈里，当 $\text{DFS}$ 遍历到 $v$，而且已经遍历完 $v$ 所能直接到达的顶点时， $low _ v = dfn _ v$ 时，$v$ 一定能到达栈里 $v$ 上面的顶点：因为当 $\text{DFS}$ 遍历到 $v$，而且已经 $\text{DFS}$ 递归调用完 $v$ 所能直接到达的顶点时（假设上面没有 $low=dfn$），这时如果发现 $low _ v = dfn _ v$，栈上面的顶点一定是刚才从顶点 $v$ 递归调用时进栈的，所以 $v$ 一定能够到达那些顶点。
$\text{DFS}$ 遍历时，如果已经遍历完 $v$ 所能直接到达的顶点而 $low _ v = dfn _ v$，我们知道 $v$ 一定能到达栈里 $v$ 上面的顶点，这些顶点的 $low$ 一定小于自己的 $dfn$，不然就会出栈了，也不会小于 $dfn _ v$,不然 $low _ v$ 一定小于 $dfn _ v$,所以栈里 $v$ 以其 $v$ 以上的顶点组成的子图是一个强连通分量，如果它不是极大强连通分量的话 $low _ v$ 也一定小于 $dfn _ v$（这里不再详细说），所以栈里 $v$ 以其 $v$ 以上的顶点组成的子图是一个极大强连通分量。
若存在边 $<i, j>$ 且遍历到它的时候 $j$ 在栈中，那么 $i$ 和 $j$ 可能存在三种关系：

$i$ 是 $j$ 的祖先；
$j$ 是 $i$ 的祖先；
$i$ 和 $j$ 无前后关系。

对于情况 $1$，必有 $dfn _ j > dfn _ i$，因此不必考虑；
对于情况 $2$，$<i, j>$ 是逆向边，显然 $i$、$j$ 处于同一个强连通分支；
对于情况 $3$，$<i, j>$ 是横叉边，显然 $i$、$j$ 必然在同一棵搜索树中（因为搜索树的根结点肯定满足 $low = dfn$），设 $p=lca(i, j)$，由于从 $p$ 到 $j$ 的路径上木有 $low = dfn$ 的结点（否则 $j$ 已经出栈了），所以 $j$ 必然可以到达 $p$，又因为 $p$ 可以到达 $i$，所以 $j$ 也可以到达 $i$，又因为存在边 $<i, j>$，所以 $i$、$j$ 处于同一个强连通分支，这样就需要在计算 $low _ i$ 的时候把 $dfn _ j$ 考虑进去，而不能让 $i$ 及其所有后代成为一个强连通分支。

应用

缩点

根据强联通分量的强连通性，我们可以将其缩为一个点，将整张图变为一个 $\text{DAG}$，然后方便进行拓扑排序等后续算法。

求割点和桥

$\text{Tarjan}$ 的拓展用法之一。

附

强联通分量还可以用 $\text{Korasaju}$ 算法求解，这里主要学习的是 $\text{Tarjan}$ 算法，故不做介绍。感兴趣可以自行搜索学习。

参考

强连通分量的Tarjan算法
算法学习笔记(69):强连通分量（推荐学习一下，$\text{Tarjan}$ 算法实现的具体过程）
强连通分量 - OI Wiki

posted @ 2024-01-07 16:05 Foiled 阅读(127) 评论(0) 编辑收藏举报

刷新页面返回顶部

Fioled 的博客

天空没有翅膀的痕迹，而我已飞过

强连通分量(Tarjan)

强联通分量与 \(\text{Tarjan}\)（求解）

定义

处理

时间戳：\(dfn_i\)

追溯值：\(low_i\)

计算追溯值（寻找强连通分量的基本功）

\(\text{Tarjan}\) 算法求强连通分量

伪代码参考

代码实现

注意

\(\text{Tarjan}\) 算法的操作原理

\(\text{Tarjan}\) 算法的大致证明

应用

缩点

求割点和桥

附

参考

公告