二分图

二分图的概念

定义：二分图（\(\text{Bipartite\ Graph}\)）

如果一张无向图的 \(N\) 个节点可以分成 \(A,B\) 两个不相交的非空集合，并且同集合内的点之间没有边相连，那么称该无向图为二分图(\(\text{Bipartite\ Graph}\))。

性质：二分图不存在长度为奇数的环

因为每一条边都是从一个集合走到另一个集合。既然要形成环，必须回到出发点，也就是要回到出发点所在的集合。只有走偶数次才可能回到同一个集合。
事实上，这个条件是充分必要的。即一张无向图是二分图, 当且仅当图中不存在奇环(长度为奇数的环)。

二分图判定

染色法

思路

根据“二分图不存在长度为奇数的环”这一性质，可以用两种颜色标记图中的节点，当一个点被标记后，所有与它相邻的节点应该标记与它相反的颜色，若标记过程产生冲突，则说明图中存在奇环。

实现

用 \(\text{DFS}\) 或 \(\text{BFS}\) 来实现。
\(color _ i\)初始化为 \(0\)，被访问的点的颜色是 \(1\) 或 \(2\)。
枚举没有被染色的点 \(\u\)

1. 对 \(u\) 点染色
2. 枚举 \(u\) 的邻点 \(v\)
   (1) 若 \(v\) 未访问，则访问若返回有奇环，则一路返回有奇环。
   (2) 若 \(v\) 已访问，判断 \(v\) 的颜色与 \(u\) 的颜色是否相同，若相同则返回有奇环。
3. 枚举完 \(u\) 的邻点，没有发现奇环，则返回没有奇环。

时间复杂度：\(O(n+m)\)

代码

#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;
const int N = 100010, M = 2 * N;
int n, m;
struct edge {
	int v, ne;
} e[M];
int h[N], idx;
int color[N];
void add(int a, int b) {
	e[++idx] = {b, h[a]};
	h[a] = idx;
}
bool dfs(int u, int c) {
	color[u] = c;
	for (int i = h[u]; i; i = e[i].ne) {
		int v = e[i].v;
		if (!color[v]) {
			if (dfs(v, 3 - c))return 1;
		} else if (color[v] == c)return 1; //有奇环
	}
	return 0;
}
int main() {
	cin >> n >> m;
	for (int i = 0; i < m; i++) {
		int a, b;
		cin >> a >> b;
		add(a, b);
		add(b, a);
		bool flag = 0;
		for (int i = 1; i <= n; i++)
			if (!color[i])
				if (dfs(i, 1)) {
					flag = 1; //有奇环
					break;
				}
		if (flag) puts("No");
		else puts("Yes");
		return 0;
	}

二分图最大匹配（\(\text{Maximum\ Matching}\)）

概念

极大匹配 (\(\text{Maximal\ Matching}\))是指在当前已完成的匹配下，无法再通过增加未完成匹配的边的方式来增加匹配的边数。
最大匹配 (\(\text{maximum\ matching}\))是所有极大匹配当中边数最大的一个匹配。

二分图最大匹配问题的定义

二分图最大匹配问题，就是在 \(A\)、\(B\) 这两个集合中，不断选择两个存在连线的点，把他们连起来，求最多可以有多少条连线的问题。

匈牙利算法（\(\text{Hungarian\ algorithm}\)）

思路

交替路（\(\text{alternating\ path}\)）

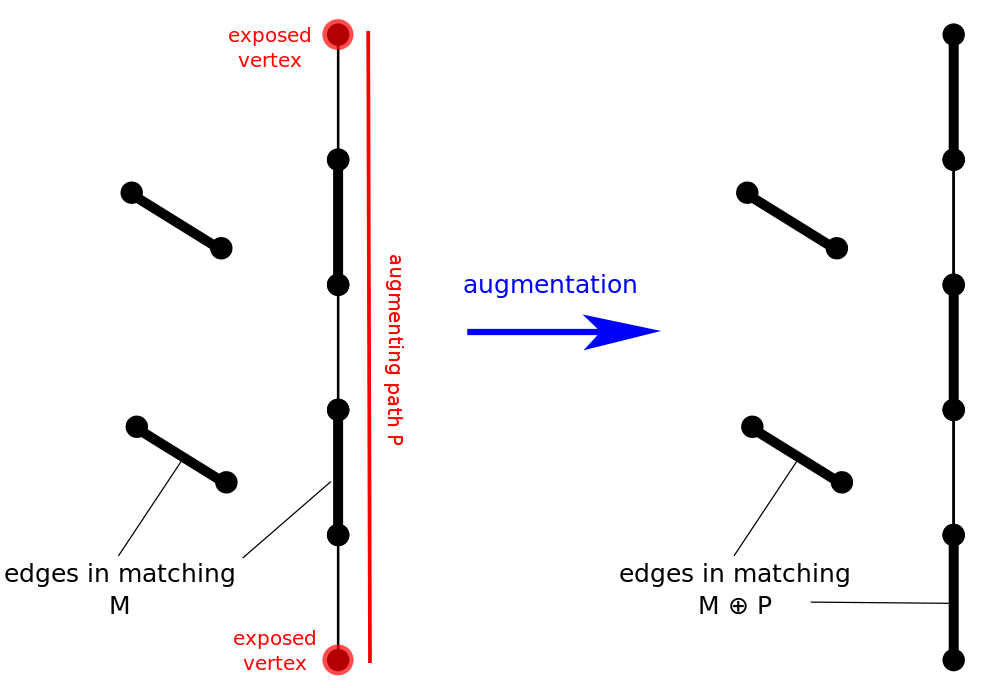
从一个末匹配点出发，依次经过非匹配边、匹配边、非匹配边 \(\cdots\) 形成的路径叫交替路。

增广路（\(\text{augmenting\ path}\)）

从一个末匹配点出发，走交替路，若能到达另一个末匹配点，则这条交替路称为增广路。例如：\(8 \rightarrow 4 \rightarrow 7 \rightarrow 1 \rightarrow 5 \rightarrow 2\)

增广的过程

思路

观察增广路，我们会发现: 非匹配边比匹配边多一条。只要把增广路中的匹配边和非匹配边的身份交换（即倒过来走），交换后，图中的匹配边数目比原来多了 \(1\) 条。

所以，这里的“增广”路的含义就是指能增加匹配边的一条路。

匈牙利算法就是通过不停地找增广路来增加匹配边。找不到增广路时，达到最大匹配。

实现

可以用 \(\text{DFS}\) 或 \(\text{BFS}\) 来实现。这里通过男女配对问题进行说明。

\(vis _ v\)：女生v是否访问
\(match _ v\)：存女生v的男友
枚举 \(n\) 个男生，每轮 \(vis _ i\) 初始化为 \(0\) (即女生皆可选)
\(\text{DFS}\) 若能配成对，\(ans++\)。
\(\text{DFS}\) 过程:返回男生 \(u\) 能不能配对到一个女生
枚举男生 \(u\) 的心仪女生 \(v\)

1. 若女生已标记，则跳过。
2. 若女生没男友，则配成对;
3. 若女生的男友可以换掉，则配成对。
   返回 \(\text{true}\)

枚举完 \(u\) 的心仪女生，都不能配成对，则返回 \(\text{false}\)。

这么做，就实现了上面说的“通过不停地找增广路来增加匹配边”。

时间复杂度：访问 \(n\) 个点，每个点最多遍历 \(m\) 条边，时间复杂度 \(O(nm)\)，但实际运行过程中不会遍历到 \(m\) 条边，所以会快很多。

代码

// Luogu P3386 【模板】二分图最大匹配
#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;
const int N = 505, M = 100010;
int n, m, k, a, b, ans;
struct edge {
	int v, ne;
} e[M];
int h[N], idx;
int vis[N], match[N];
void add(int a, int b) {
	e[++idx] = {b, h[a]};
	h[a] = idx;
}
bool dfs(int u) {
	for (int i = h[u]; i; i = e[i].ne) {
		int v = e[i].v; //妹子
		if (vis[v])
			continue;
		vis[v] = 1; //先标记这个妹子
		if (!match[v] || dfs(match[v])) {
			match[v] = u; //配成对
			return 1;
		}
	}
	return 0;
}
int main() {
	cin >> n >> m >> k;
	for (int i = 0; i < k; i++)
		cin >> a >> b, add(a, b);
	for (int i = 1; i <= n; i++) {
		memset(vis, 0, sizeof vis);
		if (dfs(i))
			ans++;
	}
	cout << ans;
	return 0;
}

\(\text{Dinic}\) 算法

思路

二分图最大匹配可以转换成网络流模型。
将源点连上左边所有点，右边所有点连上汇点，容量皆为 \(1\)。原来的每条边从左往右连边，容量也皆为 \(1\)，最大流即最大匹配。
如果使用 \(\text{Dinic}\) 算法 求该网络的最大流，可在 \(O(\sqrt{n}m)\) 求出。
\(\text{Dinic}\) 算法分成两部分，第一部分用 \(O(m)\) 时间 \(\text{BFS}\) 建立网络流，第二步是 \(O(nm)\) 时间 \(\text{DFS}\) 进行增广。
但因为容量为 \(1\)，所以实际时间复杂度为 \(O(m)\)。
接下来前 \(O(\sqrt{n})\) 轮，复杂度为 \(O(\sqrt{n}m)\)。\(O(\sqrt{n})\) 轮以后，每条增广路径长度至少 \(\sqrt{n}\)，而这样的路径不超过 \(\sqrt{n}\)，所以此时最多只需要跑 \(\sqrt{n}\) 轮，整体复杂度为 \(O(\sqrt{n}m)\)。

算法思想(\(\text{Dinic}\))

考虑在增广前先对 \(G _ f\) 做 \(\text{BFS}\) 分层，即根据结点 \(u\) 到源点 \(s\) 的距离 \(d(u)\) 把结点分成若干层。令经过 \(u\) 的流量只能流向下一层的结点 \(v\)，即删除 \(u\) 向层数标号相等或更小的结点的出边，我们称 \(G _ f\) 剩下的部分为层次图（\(\text{Level\ Graph}\)）。形式化地，我们称 \(G _ L = (V, E _ L)\) 是 \(G _ f = (V, E _ f)\) 的层次图，其中 \(E _ L = \left\{ (u, v) \mid (u, v) \in \ E _ f, d(u) + 1 = d(v) \right\}\)。

如果我们在层次图 \(G _ L\) 上找到一个最大的增广流 \(f _ b\)，使得仅在 \(G _ L\) 上是不可能找出更大的增广流的，则我们称 \(f _ b\) 是 \(G _ L\) 的阻塞流（\(\text{Blocking\ Flow}\)）。

Warning

尽管在上文中我们仅在单条增广路上定义了增广/增广流，广义地，「增广」一词不仅可以用于单条路径上的增广流，也可以用于若干增广流的并——后者才是我们定义阻塞流时使用的意义。

定义层次图和阻塞流后，\(\text{Dinic}\) 算法的流程如下。

在 \(G _ f\) 上 \(\text{BFS}\) 出层次图 \(G _ L\)。
在 \(G _ L\) 上 \(\text{DFS}\) 出阻塞流 \(f _ b\)。
将 \(f _ b\) 并到原先的流 \(f\) 中，即 \(f \leftarrow f + f _ b\)。
重复以上过程直到不存在从 \(s\) 到 \(t\) 的路径。
此时的 \(f\) 即为最大流。

在分析这一算法的复杂度之前，我们需要特别说明「在 \(G _ L\) 上 \(\text{DFS}\) 出阻塞流 \(f _ b\)」的过程。尽管 \(\text{BFS}\) 层次图对于本页面的读者应当是 \(\text{trivial}\) 的，但 \(\text{DFS}\) 阻塞流的过程则稍需技巧——我们需要引入当前弧优化。

注意到在 \(G_L\) 上 \(\text{DFS}\) 的过程中，如果结点 \(u\) 同时具有大量入边和出边，并且 \(u\) 每次接受来自入边的流量时都遍历出边表来决定将流量传递给哪条出边，则 \(u\) 这个局部的时间复杂度最坏可达 \(O(|E|^2)\)。为避免这一缺陷，如果某一时刻我们已经知道边 \((u, v)\) 已经增广到极限（边 \((u, v)\) 已无剩余容量或 \(v\) 的后侧已增广至阻塞），则 \(u\) 的流量没有必要再尝试流向出边 \((u, v)\)。据此，对于每个结点 \(u\)，我们维护 \(u\) 的出边表中第一条还有必要尝试的出边。习惯上，我们称维护的这个指针为当前弧，称这个做法为当前弧优化。

多路增广

多路增广是 \(\text{Dinic}\) 算法的一个常数优化——如果我们在层次图上找到了一条从 \(s\) 到 \(t\) 的增广路 \(p\)，则接下来我们未必需要重新从 \(s\) 出发找下一条增广路，而可能从 \(p\) 上最后一个仍有剩余容量的位置出发寻找一条岔路进行增广。考虑到其与回溯形式的一致性，这一优化在 \(\text{DFS}\) 的代码实现中也是自然的。

常见误区

可能是由于大量网络资料的错误表述引发以讹传讹的情形，相当数量的选手喜欢将当前弧优化和多路增广并列称为 \(\text{Dinic}\) 算法的两种优化。实际上，当前弧优化是用于保证 \(\text{Dinic}\) 时间复杂度正确性的一部分，而多路增广只是一个不影响复杂度的常数优化。

时间复杂度分析

应用当前弧优化后，对 \(\text{Dinic}\) 算法的时间复杂度分析如下。

首先，我们尝试证明单轮增广中 \(\text{DFS}\) 求阻塞流的时间复杂度是 \(O(|V||E|)\)。

单轮增广的时间复杂度的证明

考虑阻塞流 \(f_b\) 中的每条增广路，它们都是在 \(G_L\) 上每次沿当前弧跳转而得到的结果，其中每条增广路经历的跳转次数不可能多于 \(|V|\)。

每找到一条增广路就有一条饱和边消失（剩余容量清零）。考虑阻塞流 \(f_b\) 中的每条增广路，我们将被它们清零的饱和边形成的边集记作 \(E_1\)。考虑到 \(G_L\) 分层的性质，饱和边消失后其反向边不可能在同一轮增广内被其他增广路经过，因此，\(E_1\) 是 \(E_L\) 的子集。

此外，对于沿当前弧跳转但由于某个位置阻塞所以没有成功得到增广路的情形，我们将这些不完整的路径上的最后一条边形成的边集记作 \(E_2\)。\(E_2\) 的成员不饱和，所以 \(E_1\) 与 \(E_2\) 不交，且 \(E_1 \cup E_2\) 仍是 \(E_L\) 的子集。

由于 \(E_1 \cup E_2\) 的每个成员都没有花费超过 \(|V|\) 次跳转（且在使用多路增广优化后一些跳转将被重复计数），因此，综上所述，\(\text{DFS}\) 过程中的总跳转次数不可能多于 \(|V||E_L|\)。

常见伪证一则

对于每个结点，我们维护下一条可以增广的边，而当前弧最多变化 \(|E|\) 次，从而单轮增广的最坏时间复杂度为 \(O(|V||E|)\)。

Bug

「当前弧最多变化 \(|E|\) 次」并不能推得「每个结点最多访问其出边 \(|E|\) 次」。这是因为，访问当前弧并不一定耗尽上面的剩余容量，结点 \(u\) 可能多次访问同一条当前弧。

注意到层次图的层数显然不可能超过 \(|V|\)，如果我们可以证明层次图的层数在增广过程中严格单增，则 \(\text{Dinic}\) 算法的增广轮数是 \(O(|V|)\) 的。接下来我们尝试证明这一结论2。

层次图层数单调性的证明

我们需要引入预流推进类算法（另一类最大流算法）中的一个概念——高度标号。为了更方便地结合高度标号表述我们的证明，在证明过程中，我们令 \(d_f(u)\) 为 \(G_f\) 上结点 \(u\) 到 汇点 \(t\) 的距离，从 汇点 而非源点出发进行分层（这并没有本质上的区别）。对于某一轮增广，我们用 \(f\) 和 \(f'\) 分别表示增广前的流和增广后的流。在该轮增广中求解并加入阻塞流后，记层次图由 \(G_L = (V, E_L)\) 变为 \(G'_ {L} = (V, E'_ L)\)。

我们给高度标号一个不严格的临时定义——在网络 \(G = (V, E)\) 上，令 \(h\) 是点集 \(V\) 到整数集 \(N\) 上的函数，\(h\) 是 \(G\) 上合法的高度标号当且仅当 \(h(u) \leq h(v) + 1\) 对于 \((u, v) \in E\) 恒成立。

考察所有 \(E_{f'}\) 的成员 \((u, v)\)，我们发现 \((u, v) \in E_{f'}\) 的原因是以下二者之一。

\((u, v) \in E_f\)，且剩余容量在该轮增广过程中未耗尽——根据最短路的定义，此时我们有 \(d_f(u) \leq d_f(v) + 1\)；
\((u, v) \not \in E_f\)，但在该轮增广过程中阻塞流经过 \((v, u)\) 并退流产生反向边——根据层次图和阻塞流的定义，此时我们有 \(d_f(u) + 1 = d_f(v)\)。
以上观察让我们得出一个结论——\(d_f\) 在 \(G_{f'}\) 上是一个合法的高度标号。当然，在 \(G_{f'}\) 的子图
\(G'_ L\) 上也是。

现在，对于一条 \(G'_ L\) 上的增广路 \(p = (s, \dots, u, v, \dots, t)\)，按照 \(p\) 上结点的反序（从 \(t\) 到 \(s\) 的顺序）考虑从空路径开始每次添加一个结点的过程。假设结点 \(v\) 已加入，结点 \(u\) 正在加入，我们发现，加入结点 \(u\) 后，根据层次图的定义，\(d_{f'}(u)\) 的值较 \(d_{f'}(v)\) 增加 \(1\)；与此同时，由于 \(d_f\) 是 \(G'_ L\) 上的高度标号，\(d_f(u)\) 的值既可能较 \(d_f(v)\) 增加 \(1\)，也可能保持不变或减少。因此，在整条路径被添加完成后，我们得到 \(d_{f'}(s) \geq d_f(s)\)，其中取等的充要条件是 \(d_f(u) = d_f(v) + 1\) 对于 \((u, v) \in p\) 恒成立。如果该不等式不能取等，则有 \(d_{f'}(s) > d_f(s)\)——即我们想要的结论「层次图的层数在增广过程中严格单增」。以下我们尝试证明该不等式不能取等。

考虑反证，我们假设 \(d_{f'}(s) = d_f(s)\) 成立，并尝试导出矛盾。现在我们断言，在 \(G'_ L\) 上，p 至少包含一条边 \((u, v)\) 满足 \((u, v)\) 在 \(G_L\) 上不存在。如果没有这样的边，考虑到 \(d_f(s) = d_{f'}(s)\)，结合层次图和阻塞流的定义，\(G_L\) 上的增广应尚未完成。为了不产生以上矛盾，我们的断言只好是正确的。

令 \((u, v)\) 是满足断言条件的那条边，其满足断言的原因只能是以下二者之一。

\((u, v) \in E_f\) 但 \(d_f(u) \leq d_f(v) + 1\) 未取等，故根据层次图的定义可知 \((u, v) \not \in E_L\)，并在增广后新一轮重分层中被加入到
\(E'_ L\) 中；
\((u, v) \not \in E _ f\)，这意味着 \((u, v)\) 这条边的产生是当前轮次增广中阻塞流经过 \((v, u)\) 并退流产生反向边的结果，也即 \(d_f(u) = d_f(v) - 1\)。
由于我们无论以何种方式满足断言均得到 \(d_f(u) \neq d_f(v) + 1\)，也即 \(d_{f'}(s) \geq d_f(s)\) 取等的充要条件无法被满足，这与反证假设 \(d_{f'}(s) = d_f(s)\) 冲突，原命题得证。

常见伪证另一则

考虑反证。假设层次图的层数在一轮增广结束后较原先相等，则层次图上应仍存在至少一条从 \(s\) 到 \(t\) 的增广路满足相邻两点间的层数差为 \(1\)。这条增广路未被增广说明该轮增广尚未结束。为了不产生上述矛盾，原命题成立。

Bug

「一轮增广结束后新的层次图上 \(s-t\) 最短路较原先相等」并不能推得「旧的层次图上该轮增广尚未结束」。这是因为，没有理由表明两张层次图的边集相同，新的层次图上的 \(s-t\) 最短路有可能经过旧的层次图上不存在的边。

将单轮增广的时间复杂度 \(O(|V||E|)\) 与增广轮数 \(O(|V|)\) 相乘，\(\text{Dinic}\) 算法的时间复杂度是 \(O(|V|^2|E|)\)。

如果需要令 \(\text{Dinic}\) 算法的实际运行时间接近其理论上界，我们需要构造有特殊性质的网络作为输入。由于在算法竞赛实践中，对于网络流知识相关的考察常侧重于将原问题建模为网络流问题的技巧。此时，我们的建模通常不包含令 \(\text{Dinic}\) 算法执行缓慢的特殊性质；恰恰相反，\(\text{Dinic}\) 算法在大部分图上效率非常优秀。因此，网络流问题的数据范围通常较大，「将 \(|V|, |E|\) 的值代入 \(|V|^2|E|\) 以估计运行时间」这一方式并不适用。实际上，进行准确的估计需要选手对 \(\text{Dinic}\) 算法的实际效率有一定的经验，读者可以多加练习。

特殊情形下的时间复杂度分析

在一些性质良好的图上，\(\text{Dinic}\) 算法有更好的时间复杂度。

对于网络 \(G = (V, E)\)，如果其所有边容量均为 \(1\)，即 \(c(u, v) \in \{0, 1\}\) 对于 \((u, v) \in E\) 恒成立，则我们称 \(G\) 是单位容量（\(\text{Unit\ Capacity}\)）的。

1. 在单位容量的网络中，\(\text{Dinic}\) 算法的单轮增广的时间复杂度为 \(O(|E|)\)。

证明
这是因为，每次增广都会导致增广路上的所有边均饱和并消失，故单轮增广中每条边只能被增广一次。

2. 在单位容量的网络中，\(\text{Dinic}\) 算法的增广轮数是 \(O(|E|^{\frac{1}{2}})\) 的。

证明
以源点 \(s\) 为中心分层，记 \(d_f(u)\) 为 \(G_f\) 上结点 \(u\) 到源点 \(s\) 的距离。另外，我们定义将点集 \(\left\{u \mid u \in V, d_f(u) = k \right\}\) 定义为编号为 \(k\) 的层次 \(D_k\)，并记 \(S_k = \cup_{i \leq k}\ D_i\)。
假设我们已经进行了 \(|E|^{\frac{1}{2}}\) 轮增广。根据鸽巢原理，至少存在一个 \(k\) 满足边集 \(\left\{ (u, v) \mid u \in D_k, v \in D_{k+1}, (u, v) \in E_f \right\}\) 的大小不超过 \(\frac {|E|} {|E|^{\frac{1}{2}}} \approx |E|^{\frac{1}{2}}\)。显然，\(\{S_k, V - S_k\}\) 是 \(G_f\) 上的 \(s-t\) 割，且其割容量不超过 \(|E|^{\frac{1}{2}}\)。根据最大流最小割定理，\(G_f\) 上的最大流不超过 \(|E|^{\frac{1}{2}}\)，也即 G_f 上最多还能执行 \(|E|^{\frac{1}{2}}\) 轮增广。因此，总增广轮数是 \(O(|E|^{\frac{1}{2}})\) 的。

3. 在单位容量的网络中，\(\text{Dinic}\) 算法的增广轮数是 \(O(|V|^{\frac{2}{3}})\) 的。

证明
假设我们已经进行了 \(2 |V|^{\frac{2}{3}}\) 轮增广。由于至多有半数的（\(|V|^{\frac{2}{3}}\) 个）层次包含多于 \(|V|^{\frac{1}{3}}\) 个点，故无论我们如何分配所有层次的大小，至少存在一个 \(k\) 满足相邻两个层次同时包含不多于 \(|V|^{\frac{1}{3}}\) 个点，即 \(|D_k| \leq |V|^{\frac{1}{3}}\) 且 \(|D_{k+1}| \leq |V|^{\frac{1}{3}}\)。
为最大化 \(D_k\) 和 \(D_{k+1}\) 之间的边数，我们假定这是一个完全二分图，此时边集 \(\left\{ (u, v) \mid u \in D_k, v \in D_{k+1}, (u, v) \in E_f \right\}\) 的大小不超过 \(|V|^{\frac{2}{3}}\)。显然，\(\{S_k, V - S_k\}\) 是 \(G_f\) 上的 \(s-t\) 割，且其割容量不超过 \(|V|^{\frac{2}{3}}\)。根据最大流最小割定理，\(G_f\) 上的最大流不超过 \(|V|^{\frac{2}{3}}\)，也即 \(G_f\) 上最多还能执行 \(|V|^{\frac{2}{3}}\) 轮增广。因此，总增广轮数是 \(O(|V|^{\frac{2}{3}})\) 的。

4. 在单位容量的网络中，如果除源汇点外每个结点 \(u\) 都满足 \(\mathit{deg} _ {\mathit{in}}(u) = 1\) 或 \(\mathit{deg} _ {\mathit{out}}(u) = 1\)，则 \(\text{Dinic}\) 算法的增广轮数是 \(O(|V|^{\frac{1}{2}})\) 的。其中，\(\mathit{deg} _ {\mathit{in}}(u)\) 和 \(\mathit{deg} _ {\mathit{out}}(u)\) 分别代表结点 \(u\) 的入度和出度。

证明
我们引入以下引理——对于这一形式的网络，其上的任意流总是可以分解成若干条单位流量的、点不交 的增广路。
假设我们已经进行了 \(|V|^{\frac{1}{2}}\) 轮增广。根据层次图的定义，此时任意新的增广路的长度至少为 \(|V|^{\frac{1}{2}}\)。
考虑 \(G_f\) 上的最大流的增广路分解，我们得到的增广路的数量不能多于 \(\frac {|V|} {|V|^{\frac{1}{2}}} \approx |V|^{\frac{1}{2}}\)，这意味着 \(G_f\) 上最多还能执行 \(|V|^{\frac{1}{2}}\) 轮增广。因此，总增广轮数是 \(O(|V|^{\frac{1}{2}})\) 的。

综上，我们得出一些推论。

在单位容量的网络上，\(\text{Dinic}\) 算法的总时间复杂度是 \(O(|E| \min(|E|^\frac{1}{2}, |V|^{\frac{2}{3}}))\)。

在单位容量的网络上，如果除源汇点外每个结点 u 都满足 \(\mathit{deg} _ {\mathit{in}}(u) = 1\) 或 \(\mathit{deg} _ {\mathit{out}}(u) = 1\)，\(Dinic\) 算法的总时间复杂度是 \(O(|E||V|^{\frac{1}{2}})\)。对于二分图最大匹配问题，我们常使用 \(\text{Hopcroft–Karp}\) 算法解决，而这一算法实际上是 \(\text{Dinic}\) 算法在满足上述度数限制的单位容量网络上的特例。

代码

struct MF {
  struct edge {
    int v, nxt, cap, flow;
  } e[N];
  int fir[N], cnt = 0;
  int n, S, T;
  ll maxflow = 0;
  int dep[N], cur[N];
  void init() {
    memset(fir, -1, sizeof fir);
    cnt = 0;
  }
  void addedge(int u, int v, int w) {
    e[cnt] = {v, fir[u], w, 0};
    fir[u] = cnt++;
    e[cnt] = {u, fir[v], 0, 0};
    fir[v] = cnt++;
  }
  bool bfs() {
    queue<int> q;
    memset(dep, 0, sizeof(int) * (n + 1));
    dep[S] = 1;
    q.push(S);
    while (q.size()) {
      int u = q.front();
      q.pop();
      for (int i = fir[u]; ~i; i = e[i].nxt) {
        int v = e[i].v;
        if ((!dep[v]) && (e[i].cap > e[i].flow)) {
          dep[v] = dep[u] + 1;
          q.push(v);
        }
      }
    }
    return dep[T];
  }
  int dfs(int u, int flow) {
    if ((u == T) || (!flow)) return flow;

    int ret = 0;
    for (int& i = cur[u]; ~i; i = e[i].nxt) {
      int v = e[i].v, d;
      if ((dep[v] == dep[u] + 1) &&
          (d = dfs(v, min(flow - ret, e[i].cap - e[i].flow)))) {
        ret += d;
        e[i].flow += d;
        e[i ^ 1].flow -= d;
        if (ret == flow) return ret;
      }
    }
    return ret;
  }
  void dinic() {
    while (bfs()) {
      memcpy(cur, fir, sizeof(int) * (n + 1));
      maxflow += dfs(S, INF);
    }
  }
} mf;

二分图最大权完美匹配

概念

二分图的完美匹配（\(\text{Perfect\ Matchin}g\)）

给定一张带边权的二分图，其左部、右部点数相等，均为 \(N\) 个点，如果最大匹配有 \(N\) 条边，则称二分图的完美匹配。

二分图的最大权完美匹配

二分图的边权和最大的完美匹配，称二分图的最大权完美匹配。

\(\text{KM}\)算法

即匈牙利算法\(\text{(Kuhn–Munkres Algorithm)}\)。

二分图的覆盖与独立集

最小点覆盖（\(\text{Minimum\ Vertex\ Cover}\)）

给定一张二分图，求出一个最小的点集 \(\text{S}\)，使得图中任意一条边都有至少一个端点属于 \(\text{S}\)。这个问题被称为二分图的最小点覆盖(\(\text{vertex\ cover}\))，简称最小覆盖。

\(\text{König}\) 定理

二分图最小点覆盖包含的点数等于二分图最大匹配包含的边数。

二分图最大独立集

图的独立集（\(\text{Independent\ Set}\)）和最大独立集（\(\text{Maximum Independent\ Set}\)）

通俗地讲，图的独立集就是“任意两点之间都没有边相连”的点集。包含点数最多的一个就是图的最大独立集。

团

“任意两点之间都有一条边相连”的子图被称为无向图的“团”。点数最多的团被称为图的最大团。

性质

无向图 \(G\) 的最大团等于其补图 \(G'\) 的最大独立集。

性质

设 \(G\) 是有 \(n\) 个节点的二分图，\(G\) 的最大独立集的大小等于 \(n\) 减去最大匹配数。

有向无环图的最小路径点覆盖

给定一张有向无环图，要求用尽量少的不相交的简单路径，覆盖有向无环图的所有顶点 (也就是每个顶点恰好被覆盖一次)。这个问题被称为有向无环图的最小路径点覆盖，简称“最小路径覆盖” 。

不相交指两条路径中没有相同的点

拆点二分图

设原来的有向无环图为 \(G=(V,E),N=|V|\)。把 \(G\) 中的每个点 \(x\) 拆成编号为 \(x\) 和 \(x + n\) 的两个点。建立一张新的二分图，\(1\sim n\) 作为二分图左部点，\(n + 1\sim 2n\)作为二分图右部点，对于原图的每条有向边 \((x,y)\)，在二分图的左部点 \(x\) 与右部点 \(y + n\) 之间连边。最终得到的二分图称为 \(G\) 的拆点二分图，记为 \(G2\)。

性质

有向无环图 \(G\) 的最小路径点覆盖包含的路径条数，等于 \(n\) 减去拆点二分图 \(G2\) 的最大匹配数。

最小路径可重复点覆盖

给定一张有向无环图，要求用尽量少的可相交的简单路径，覆盖有向无环图的所有顶点(也就是一个节点可以被覆盖多次)。这个问题被称为有向无环图的最小路径可重复点覆盖。在最小路径可重复点覆盖中，若两条路径 \(\cdots \rightarrow u \rightarrow p \rightarrow v \rightarrow \cdots\) 和 \(\cdots \rightarrow x \rightarrow p \rightarrow y \rightarrow \cdots\) 在点 \(p\) 相交，则我们在原图中添加一条边 \((x,y)\)，让第二条路径直接走 \(x \rightarrow y\)，就可以避免重复覆盖点。进一步地，如果我们把原图中所有间接连通的点对直接连上有向边，那么任何“有路径相交的点覆盖”一定都能转化成“没有路径相交的点覆盖”。

综上所述，有向无环图 \(G\) 的最小路径可重复点覆盖，等价于先对有向图传递闭包，得到有向无环图 \(G'\)，再在 \(G'\) 上求一般的（路径不可相交的）最小路径点覆盖。

参考资料

增广路
二分图最大匹配
二分图最大权匹配
干货｜二分图详解
381 二分图判定 染色法
382 二分图最大匹配 匈牙利算法
算法学习笔记(5)：匈牙利算法
383 二分图最大匹配 Dinic算法
二分图转为网络最大流模型
最大流-Dinic算法
384 二分图最大权完美匹配 KM算法
算法竞赛进阶指南 0x68章节 0x69章节
算法竞赛.罗勇军 10.11章节