最短路
最短路从入不了门到入土
前言
这是我的第一篇博客，为了纪念，我不打算修改格式。
最短路
最短路の性质
首先，什么是最短路？
当图的边有边权时，可以视作两点之间的距离，那么，如果出现多条路径，那么我们要求的那条距离最短的称为最短路（如下图）
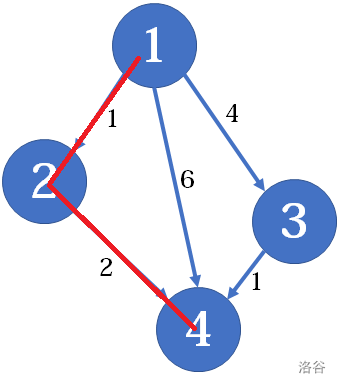
边权为正，任意两个点的最短路：
1.不会经过重复节点
2.不会经过重复边
3.任意一条的节点数不会超过n，边数不会超过n-1
好哒，相信你已经基本了解了最短路，现在来学习算法吧！
Dijkstra 算法
求解非负权图单源最短路径的算法
dijkstra的思路
从原点s开始，每次新扩展一个最近点，再以这个新点重复以上过程
dijkstra的过程
1.设dis[s]=0，其余都为+∞
2.选择dis值最小的点作为已知点，在更新所有与之相邻的点的dis值
3.重复以上操作
用邻接矩阵实现dijkstra
void dijkstra(){
foe(int i=1;i<=n;i++)
dis[i]=INF;
dis[1]=0;
for(int i=1;i<=n;i++)
{
int mark=-114514;
int mindis=INF;
for(int j=1;j<=n;j++)
{
if(vis[j]==0 && dis[j]<mindis)
{
mindis=dis[j];
mark=j;
}
}
}
vis[mark]=1;
for(int i=1;i<=n;i++)
if(vis[i]==0)
dis[j]=min(dis[i],dis[mark]+g[mark][j]);
}
用邻接表实现dijkstra
void dijkstra(){
foe(int i=1;i<=n;i++)
dis[i]=INF;
dis[1]=0;
for(int k=1;k<=n;k++)
{
int mark=-114514;
int mindis=INF;
for(int i=1;i<=n;i++)
for(int j=head[i];j;j=edge[j].next)
{
if(!vis[dege[j].to] && edge[j].dis<mindis)
{
mindis=dege[i].dis;
mark=edge[j].to;
}
}
vis[mark]=1;
for(int i=head[mark];i;i=edge[i].next)
if(!vis[edge[i].to])
dis[edge[i].to]=min(dis[edge[i].to],dis[mark]+edge[i].dis);
}
}
堆优化（其实用得不算多）
dijkstra的时间复杂度是O(n²),
如果每取一次dis值就直接让其入堆，求最短值时直接取堆顶元素即可。堆的大小是m，入堆为m log m，取出时为n long m，总的为(n+m) log n
用堆优化dijkstra
priortity_queue<pair<int,int>> q;
void dijkstra(){
memset(dis,INF,sizeof(dis));
memset(v,0,sizeof(v));
d[1]=0;
q.push(make_pair(0,1));
while(q.size())
{
int f=q.top().second;
q.pop();
if(v[f])
continue;
v[f]=1;
for(int i=head[f];;i=edge[i].next)
{
if(dis[edge[i].to]>dis[f]+edge[i].next)
{
dis[edge[i].to]=dis[x]+edge[i].dis;
q.push(make_pair(-dis[edge[i].to],edge[i].to));
}
}
}
}
题目推荐
Bellman-Ford 算法
求解单源最短路径
bellman-ford的优势
相对于无法处理边权为负值的dijkstra，bellman-ford可以处理边权为负值的情况，还可以判图中是否存在负权环
bellman-ford的过程
1.初始化d[i]=maxn，d[s]=0
2.对于边(u,v)，松弛操作对应下面的式子：dis(v)=min(dis(v),dis(u)+w(u,v))
实现bellman-ford
//自己思考，一般不用
开玩笑，我这么好心，怎么可能没有代码呢（我不会告诉你我其实不会）
struct edge {
int v, w;
};
vector<edge> e[maxn];
int dis[maxn];
const int inf = 0x3f3f3f3f;
bool bellmanford(int n, int s) {
memset(dis, 63, sizeof(dis));
dis[s] = 0;
bool flag;
for (int i = 1; i <= n; i++) {
flag = false;
for (int u = 1; u <= n; u++) {
if (dis[u] == inf) continue;
for (auto ed : e[u]) {
int v = ed.v, w = ed.w;
if (dis[v] > dis[u] + w) {
dis[v] = dis[u] + w;
flag = true;
}
}
}
if (!flag) break;
}
return flag;
}
谢谢OI Wiki的帮助
一般来说，我们会选择用SPFA优化bellman-ford，这也是我们常用的做法
SPFA的过程
1.初始化d[i]=MAXN, d[s]=0 ,队列q，源点s入队
2.从队列中求出队首元素u，并标记节点u出队，对u连接的所有节点v进行松弛操作。如果成功就检查节点v入队次数，若超过|v|则说明出现负环，算法结束；否则修改d[v]并检查节点v是否在队中，如果不在，节点v入队
3.重复第二步直到队列清空
SPFA的实现
struct edge {
int v, w;
};
vector<edge> e[maxn];
int dis[maxn], cnt[maxn], vis[maxn];
queue<int> q;
bool spfa(int n, int s) {
memset(dis, 63, sizeof(dis));
dis[s] = 0, vis[s] = 1;
q.push(s);
while (!q.empty()) {
int u = q.front();
q.pop(), vis[u] = 0;
for (auto ed : e[u]) {
int v = ed.v, w = ed.w;
if (dis[v] > dis[u] + w) {
dis[v] = dis[u] + w;
cnt[v] = cnt[u] + 1;
if (cnt[v] >= n) return false;
if (!vis[v]) q.push(v), vis[v] = 1;
}
}
}
return true;
}
题目推荐
Floyd 算法
求解任意两个结点之间的最短路
floyd的优势
适用于 任何图 ，包括有向图或无向图、边权为正或边权为负。是不是很强？
前提： 最短路必须存在
floyd的思想
对于图中两个节点S、D，SD之间最短路径有两种可能：
从S直接到达D 或 从S经过若干节点之后再到达D
floyd的过程
1.定义dp[k][i][j]表示从点i到点j只允许经过前k个点时得到的最短路径
2.如果经过第k个点，那么有dp[k][i][j]=dp[k-1][i][k]+dp[k-1][k][j]
3.如果不经过第k个点，那么dp[k][i][j]=dp[k-1][i][j]
综合：dp[k][i][j]=min(dp[k-1][i][j], dp[k-1][i][k]+dp[k-1][k][j] )
边界：dp[0][i][j]=g[i][j]，g[i][j]指i到j的边权，当无法到达时可以置为∞
floyd的实现
void floyd(){
fo(k=1;k<=n;k++)
for(i=1;i<=n;i++)
for(y=1;y<=n;y++)
f[k][i][j]=min(f[k-1][i][j],f[k-1][i][j]+f[k-1][i][j]);
}
用floyd优化floyd
证明第一维对结果无影响（不想看可以跳过）
给定第一维k的二维数组中，f[i][k]与f[k][j]在某一行和某一列,而f[i][j]则是该行和该列的交叉点上的元素。f[k][i][j]只会被用于计算f[k-1][i][j]中
所以 可以进行压缩 （你只需要看到这个就好啦！）
优化的实现
void floyd(){
for(k=1;k<=n;k++)
for(i=1;i<=n;i++)
for(y=1;y<=n;y++)
f[k][i][j]=min(f[i][j],f[x][k]+f[i][j]);
}
题目推荐
结束啦！！！
Blog by cloud_eve is licensed under CC BY-NC-SA 4.0
