比较类排序算法
算法分类
十种常见排序算法可以分为两大类:
- 比较类排序:通过比较来决定元素间的相对次序,由于其时间复杂度不能突破O(nlogn),因此也称为非线性时间比较类排序。
- 非比较类排序:不通过比较来决定元素间的相对次序,它可以突破基于比较排序的时间下界,以线性时间运行,因此也称为线性时间非比较类排序。
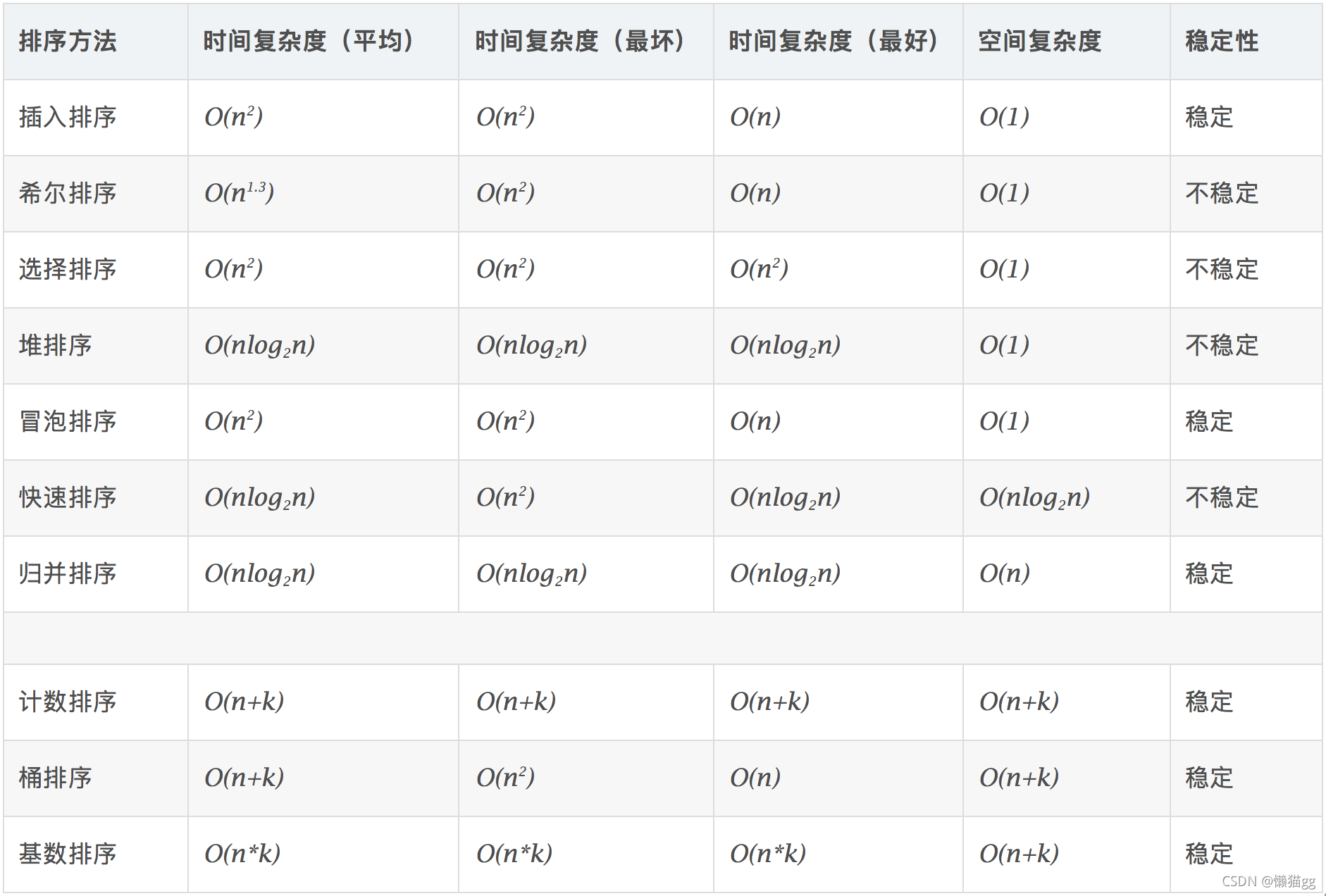
算法复杂度
一、冒泡排序
基本步骤
- 比较相邻的元素。如果第一个比第二个大,就交换它们两个;
- 对每一对相邻元素做同样的工作,从开始第一对到结尾的最后一对,这样在最后的元素就是最大的数;
- 排除最大的数,接着下一轮继续相同的操作,确定第二大的数...
- 重复步骤1-3,直到排序完成。
动图解析

Java代码
//10万个数的数组,耗时:21554毫秒
public void bubbleSort(int[] array) {
if (array == null || array.length == 0) {
return;
}
for (int i = 0; i < array.length; i++) {
// 当次循环是否发生元素交换
boolean isSwap = false;
for (int j = 0; j < array.length - 1; j++) {
int left = array[j];
int right = array[j + 1];
if (left > right) {
int temp = array[j + 1];
array[j + 1] = array[j];
array[j] = temp;
isSwap = true;
}
}
// 当次循环未发生元素交换,说明已经排好序
if (!isSwap) {
return;
}
}
}
二、快速排序(分治)
基本步骤
- 从数组中选一个数做为基准值,一般选第一个数,或者最后一个数。
- 采用双指针(头尾两端)遍历,从左往右找到比基准值大的第一个数,从右往左找到比基准值小的第一个数,交换两数位置,直到头尾指针相等或头指针大于尾指针,把基准值与头指针的数交换。这样一轮之后,左边的数就比基准值小,右边的数就比基准值大。
- 对左边的数列,重复上面1,2步骤。对右边重复1,2步骤。
- 左右两边数列递归结束后,排序完成。
动图解析

Java代码
//10万个数的数组,耗时:50毫秒
public void quickSort(int[] array) {
if (array == null || array.length == 0) {
return;
}
quickSort(array, 0, array.length - 1);
}
public void quickSort(int[] array, int low, int high) {
if (low >= high) {
return;
}
int i = low, j = high, index = array[i]; // 取最左边的数作为基准数
while (i < j) {
while (i < j && array[j] >= index) { // 向左寻找第一个小于index的数
j--;
}
if (i < j) {
array[i++] = array[j]; // 将array[j]填入array[i],并将i向右移动
}
while (i < j && array[i] < index) {// 向右寻找第一个大于index的数
i++;
}
if (i < j) {
array[j--] = array[i]; // 将array[i]填入array[j],并将j向左移动
}
}
array[i] = index; // 将基准数填入最后的坑
quickSort(array, low, i - 1); // 递归调用,分治
quickSort(array, i + 1, high); // 递归调用,分治
}
三、简单插入排序
基本步骤
- 从第一个元素开始,该元素可以认为已经被排序;
- 取出下一个元素,在前面已排序的元素序列中,从后向前扫描;
- 如果该元素(已排序)大于新元素,将该元素移到下一位置;
- 重复步骤3,直到找到已排序的元素小于或者等于新元素的位置;
- 将新元素插入到该位置后;
- 重复步骤2~5。
动图解析

Java代码
//10万个数的数组,耗时:2051毫秒
public void insertSort(int[] nums) {
if (nums == null || nums.length < 2) {
return;
}
for (int i = 0; i < nums.length - 1; i++) {
//当前值
int curr = nums[i + 1];
//上一个数的指针
int preIndex = i;
//在数组中找到一个比当前遍历的数小的第一个数
while (preIndex >= 0 && curr < nums[preIndex]) {
//把比当前遍历的数大的数字往后移动
nums[preIndex + 1] = nums[preIndex];
//需要插入的数的下标往前移动
preIndex--;
}
//插入到这个数的后面
nums[preIndex + 1] = curr;
}
}
四、希尔排序
基本步骤
把数组分割成若干(h)个小组(一般数组长度length/2),然后对每一个小组分别进行插入排序。每一轮分割的数组的个数逐步缩小,h/2->h/4->h/8,并且进行排序,保证有序。当h=1时,则数组排序完成。
解析图例

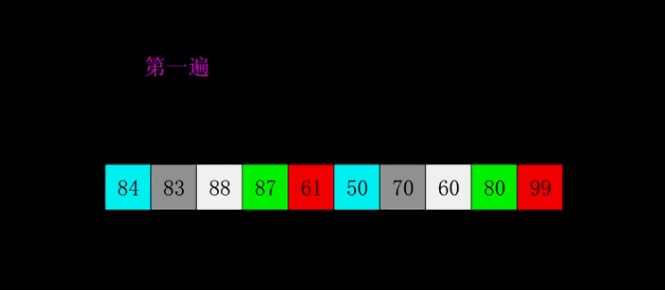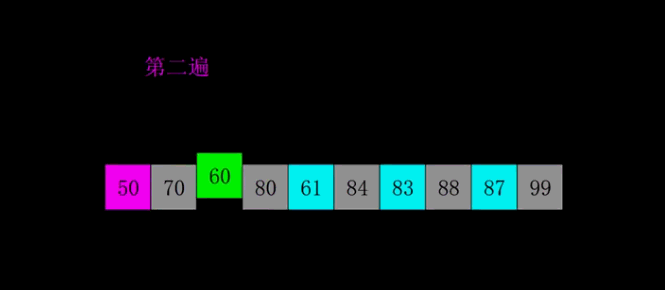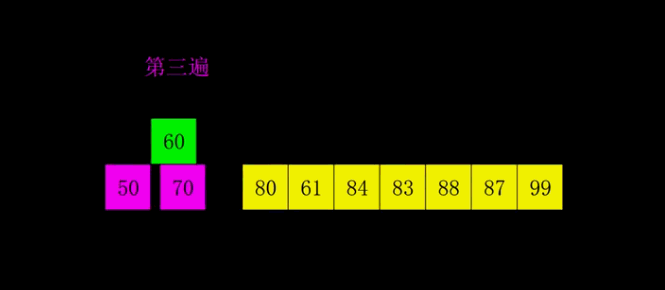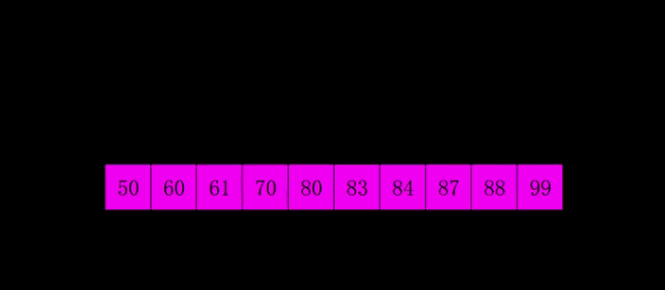
Java代码
//10万个数的数组,耗时:261毫秒
public void shellSort(int[] nums) {
if (nums == null || nums.length < 2) {
return;
}
int length = nums.length;
int temp;
//步长
int gap = length / 2;
while (gap > 0) {
for (int i = gap; i < length; i++) {
temp = nums[i];
int preIndex = i - gap;
while (preIndex >= 0 && nums[preIndex] > temp) {
nums[preIndex + gap] = nums[preIndex];
preIndex -= gap;
}
nums[preIndex + gap] = temp;
}
gap /= 2;
}
}
五、简单选择排序
基本步骤
- 第一轮,找到最小的元素,和数组第一个数交换位置。
- 第二轮,找到第二小的元素,和数组第二个数交换位置...
- 直到最后一个元素,排序完成。
动图解析
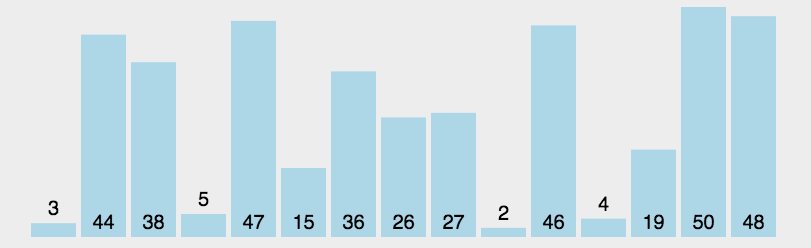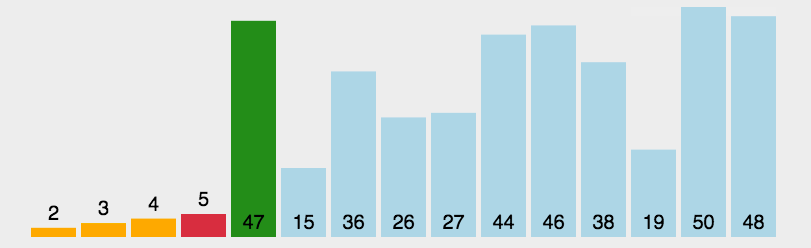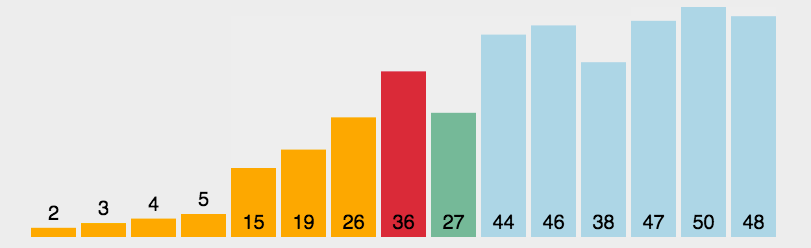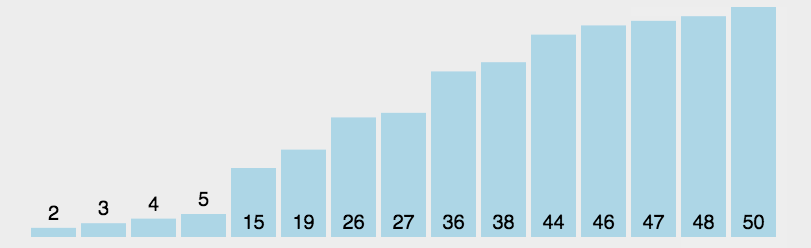
Java代码
//10万个数的数组,耗时:8492毫秒
public void selectSort(int[] nums) {
for (int i = 0; i < nums.length; i++) {
int minIndex = i;
for (int j = i + 1; j < nums.length; j++) {
if (nums[j] < nums[minIndex]) {
minIndex = j;
}
}
if (minIndex != i) {
int temp = nums[i];
nums[minIndex] = temp;
nums[i] = nums[minIndex];
}
}
}
六、堆排序
大顶堆概念:每个节点的值都大于或者等于它的左右子节点的值,所以顶点的数就是最大值。
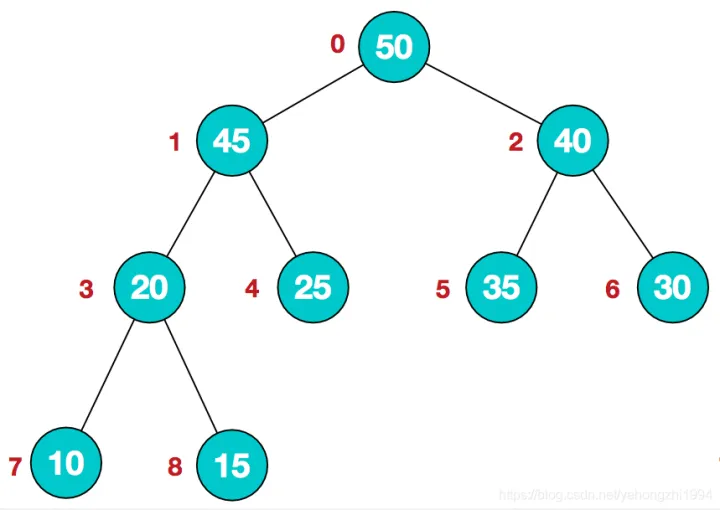
基本步骤
- 对原数组构建成大顶堆。
- 交换头尾值,尾指针索引减一,固定最大值。
- 重新构建大顶堆。
- 重复步骤2~3,直到最后一个元素,排序完成。
动图解析

Java代码
public static void sort(int[] arr) {
//1.构建大顶堆
for (int i = arr.length / 2 - 1; i >= 0; i--) {
//从第一个非叶子结点从下至上,从右至左调整结构
adjustHeap(arr, i, arr.length);
}
//2.调整堆结构+交换堆顶元素与末尾元素
for (int j = arr.length - 1; j > 0; j--) {
//将堆顶元素与末尾元素进行交换
int temp = arr[0];
arr[0] = arr[j];
arr[j] = temp;
adjustHeap(arr, 0, j);//重新对堆进行调整
}
}
public static void adjustHeap(int[] arr, int i, int length) {
int temp = arr[i];//先取出当前元素i
for (int k = i * 2 + 1; k < length; k = k * 2 + 1) {//从i结点的左子结点开始,也就是2i+1处开始
if (k + 1 < length && arr[k] < arr[k + 1]) {//如果左子结点小于右子结点,k指向右子结点
k++;
}
if (arr[k] > temp) {//如果子节点大于父节点,将子节点值赋给父节点(不用进行交换)
arr[i] = arr[k];
i = k;
} else {
break;
}
}
arr[i] = temp;//将temp值放到最终的位置
}
七、二路归并排序(分治)
归并排序是采用分治法的典型应用,而且是一种稳定的排序方式,不过需要使用到额外的空间。
归并排序的优点在于最好情况和最坏的情况的时间复杂度都是O(nlogn),所以是比较稳定的排序方式。
基本步骤
- 把数组不断划分成子序列,划成长度只有2或者1的子序列。
- 然后利用临时数组,对子序列进行排序,合并,再把临时数组的值复制回原数组。
- 反复操作1~2步骤,直到排序完成。
动图解析
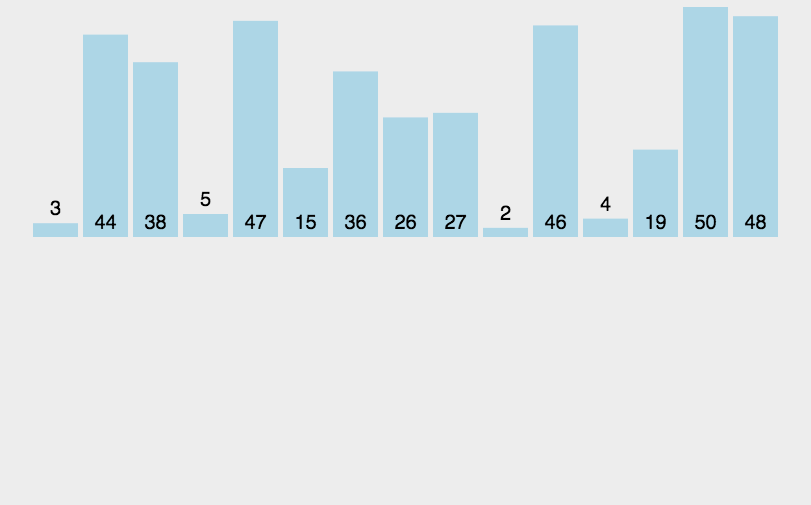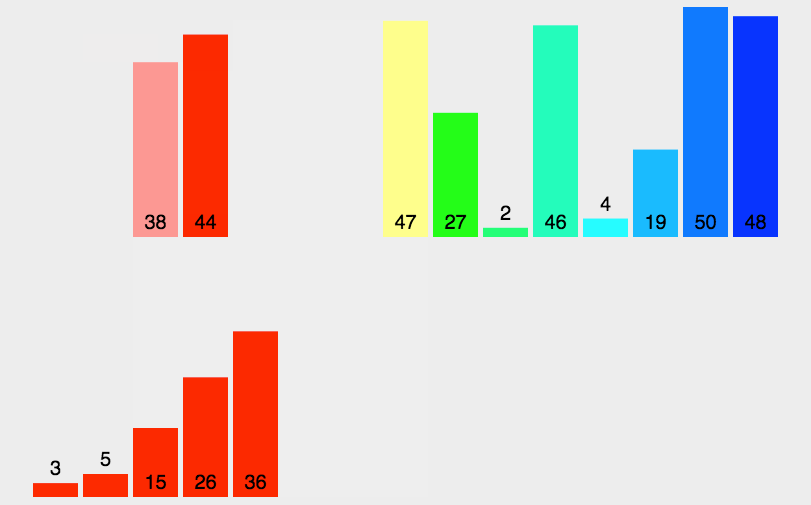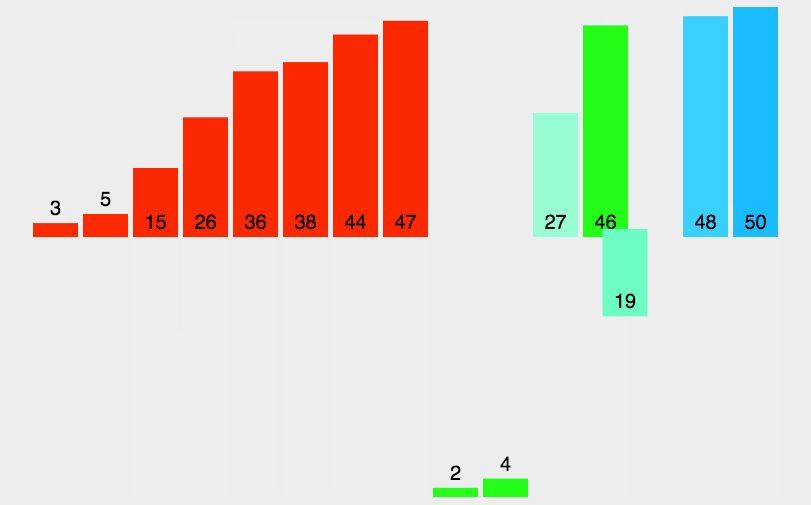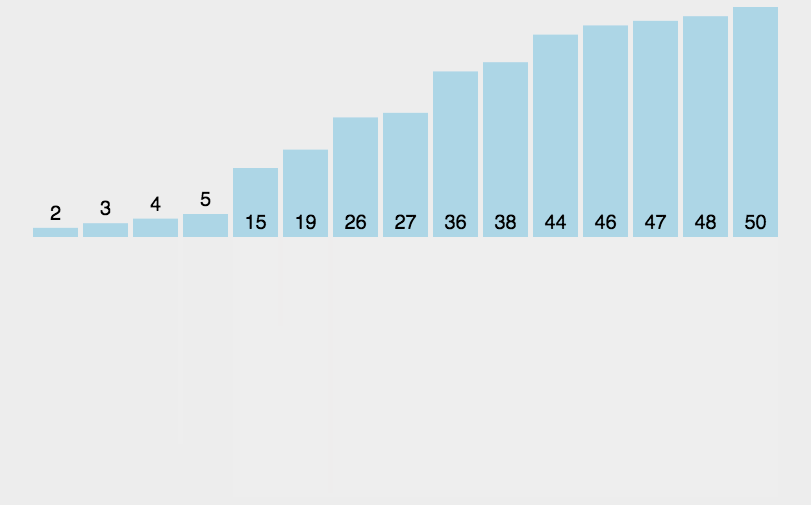
Java代码
//10万个数的数组,耗时:26毫秒
protected void sort(int[] nums) {
if (nums == null || nums.length < 2) {
return;
}
//归并排序
mergeSort(0, nums.length - 1, nums, new int[nums.length]);
}
private void mergeSort(int star, int end, int[] nums, int[] temp) {
//递归终止条件
if (star >= end) {
return;
}
int mid = star + (end - star) / 2;
//左边进行归并排序
mergeSort(star, mid, nums, temp);
//右边进行归并排序
mergeSort(mid + 1, end, nums, temp);
//合并左右
merge(star, end, mid, nums, temp);
}
private void merge(int star, int end, int mid, int[] nums, int[] temp) {
int index = 0;
int i = star;
int j = mid + 1;
while (i <= mid && j <= end) {
if (nums[i] > nums[j]) {
temp[index++] = nums[j++];
} else {
temp[index++] = nums[i++];
}
}
while (i <= mid) {
temp[index++] = nums[i++];
}
while (j <= end) {
temp[index++] = nums[j++];
}
//把临时数组中已排序的数复制到nums数组中
if (index >= 0) System.arraycopy(temp, 0, nums, star, index);
}



