[动态规划] 斜率优化DP
斜率优化
斜率优化是指在一类 DP 问题中, 我们可以通过数学方法的转化, 将转移方程改写成一个只与转移方程中的某一可变状态有关的一次函数形式, 进而通过数学方法进行优化的动态规划.
经典例题: 任务安排
注意这里的三道题数据稍微不同于李书, 但 \(n\) 应该是相同的.
任务安排 \(1\)
题目描述
机器上有 \(n\) 个需要处理的任务,它们构成了一个序列。这些任务被标号为 \(1\) 到 \(n\),因此序列的排列为 \(1 , 2 , 3 \cdots n\)。这 \(n\) 个任务被分成若干批,每批包含相邻的若干任务。从时刻 \(0\) 开始,这些任务被分批加工,第 \(i\) 个任务单独完成所需的时间是 \(T_i\)。在每批任务开始前,机器需要启动时间 \(s\),而完成这批任务所需的时间是各个任务需要时间的总和。
注意,同一批任务将在同一时刻完成。每个任务的费用是它的完成时刻乘以一个费用系数 \(C_i\)。
请确定一个分组方案,使得总费用最小。
输入格式
第一行一个整数 \(n\)。 第二行一个整数 \(s\)。
接下来 \(n\) 行,每行有一对整数,分别为 \(T_i\) 和 \(C_i\),表示第 \(i\) 个任务单独完成所需的时间是 \(T_i\) 及其费用系数 \(C_i\)。
输出格式
一行,一个整数,表示最小的总费用。
对于 \(100\%\) 的数据,\(1\le n \le 5000\),\(0 \le s \le 50\),\(1\le t_i,f_i \le 100\)。
我们刚上来一般会想出一个 \(O\left(n^3\right)\) 的做法, 但显然无论从时间还是空间上都跑不过, 不再多说.
优化空间复杂度到 \(n\), 时间复杂度到 \(O\left(n^2\right)\) 的方法: 费用先行.
费用先行?
- 因为没有规定必须分多少组, 而且任务必须按照顺序完成, 前面的分组造成的时间的滞后效应会对后面每次选择都造成一个负面的贡献, 所以我们可以直接把分组造成的时间影响压到转移方程中, 而从状态中删去, 达到减小空间开销的效果.
于是乎我们有了这个方程:
其中 \(sumT\) 为时间的前缀和, \(sumC\) 为费用的前缀和, \(S\) 为分一次组造成的时间开销,
\(S\times\left(sumC\left(N\right)-sumC\left(j\right)\right)\) 指的就是因为上一次分组而造成的累计开销.
时间复杂度: 枚举 \(i\), \(j\), \(O\left(n^2\right)\).
任务安排 \(2\)
对于 \(100\%\) 数据,\(1 \le n \le 3 \times 10^5\),\(1 \le s \le 2^8\),\(T_i \le 2^8\),\(0 \le C_i \le 2^8\)。
\(O\left(n^2\right)\) 的程序在跑 \(3e5\) 的数据范围时显然有些力不从心, 我们需要考虑如何将程序进行时间复杂度上的优化.
观察该转移方程, 我们可以对其进行移项, 得到:
- 注意:我们这里把 \(\min\)去掉了,是把 \(j\) 的取值集合所映射的 \(f\left(j\right)\) 和 \(sumC\left(j\right)\) 分别作为函数的函数值和自变量.
对于这个函数, 我们不难发现, 当 \(i\) 保持不变时, 该函数是一个与 \(j\) 有关的一次函数,
它的特征如下:
- 斜率: \(sumT\left(i\right)+S\)
- 纵截距: \(f\left(i\right) - sumT\left(i\right) \times sumC\left(i\right) - S \times sumC\left(n\right)\)
所以, 我们想要最小化 \(f\left(i\right)\) 的值, 实际上就是最小化纵截距.
我们可以在函数图像( \(x轴: sumC\left(j\right), y轴 : f\left(j\right)\) )中将这个函数表示出来, 如图( 图有点丑, 见谅 ):
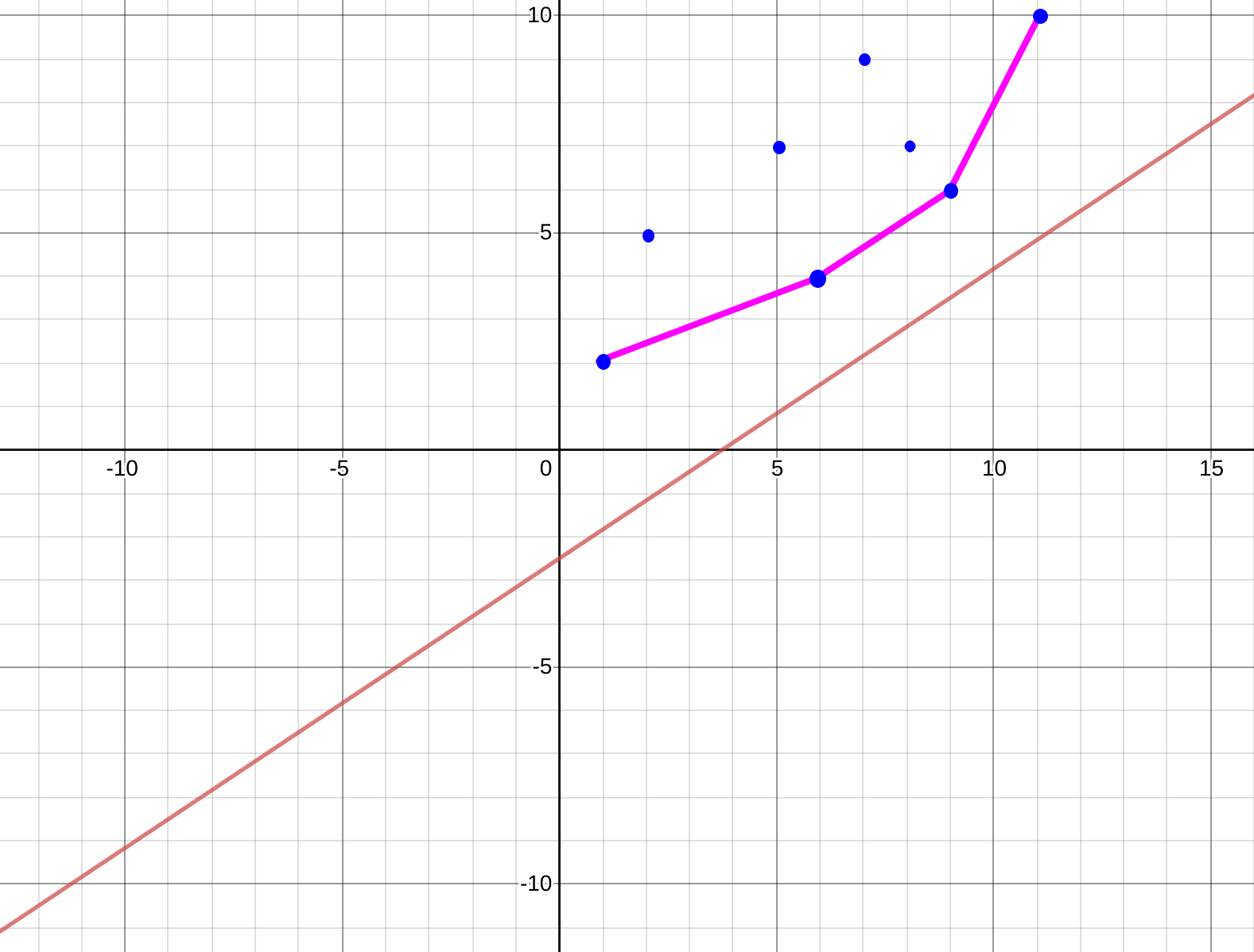
- 图中的蓝色节点表示的是每一个可以用来转移的方案, 红色直线表示任意一条斜率确定, 为 \(sumT\left(i\right)+S\) 的直线.
设这条斜率确定的直线为 \(l\), 发现我们上下移动 \(l\), 使 \(l\) 过可用的决策点时, 便可产生一种答案.
为了探究最佳决策需要满足的条件, 我们设三个决策为 \(j_1, j_2, j_3\), 且 \(j_1\lt j_2\lt j_3\).
从图中可以发现, \(j_2\) 可以成为最优决策, 当且仅当:
也就是 \(k_{j_1, j_2} \lt k_{j_2, j_3}\).
这样, 我们所需维护的答案一定是在可选方案所构成的图形的下凸壳上.
同时, 由于 \(sumC\) 单调递增, 新决策的横坐标一定大于旧决策, 又因为 \(sumT\) 单调递增, \(S + sumT\left(i\right )\), 即 \(k_l\) 单调递增, 如果我们对于凸壳上每两个相邻顶点的截距, 只保留大于 \(k_l\) 的部分, 那么最优决策一定在这个凸壳的左端点**上.
于是, 我们可以采用单调队列维护可用的决策状态( 对应图中蓝色顶点 )进行DP, 时间复杂度可以压到 \(O\left(n\right)\).
任务安排 \(3\)
对于 \(100\%\) 数据,\(1 \le n \le 3 \times 10^5\),\(1 \le s \le 2^8\),\(\left| T_i \right| \le 2^8\),\(0 \le C_i \le 2^8\)。
由于 \(T\) 可能有负数, \(sumT\) 不再单调, 所以我们需要用二分查找维护单调队列中的决策位置 \(p\), 当 \(p\) 左侧线段斜率小于 \(k_l\), 右侧线段斜率大于 \(k_l\) 时, 便为最优决策.





