流体力学基础
本文为学习王洪伟流体力学的记录
简介
气液 统称流体 ,他们的粒子之间基本无作用力
研究流体,流体与固体作用
换热器对流 香蕉球 高大建筑抗风性
对流(convection)指的是流体内部由于各部分温度不同而造成的相对流动,即流体(气体或液体)通过自身各部分的宏观流动实现热量传递的过程。 液体或气体中,较热的部分上升, 较冷的部分下降,循环流动,互相掺和,最终使温度趋于均匀。 因流体的热导率很小, 通过热传导传递的热量很少, 对流是流体的主要传热方式。
香蕉球,球飞出去的时候还带旋转,在空中受到了水平方向的力

流体和固体力学的区别,液体气体分子排布不规则,流体内部不存在拉力,固体在静态变形时内部产生剪切力
表面张力是表面存在的拉力

着眼于物体本身进行分析和着眼于空间进行分析,欧拉倡导的,为欧拉法

研究流体进出一个空间的规律

粘性
nian 性

水珠可以贴在玻璃上,因为表面张力喝吸附力,悬臂梁结构
流体的粘性力就是流体之间的动摩擦力,流体不存在静摩擦力

无滑移条件,固体和液体没有相对运动,流体与固体的摩擦力,其实是流体内部的摩擦力,表面张力和分子间的力很重要,吸附力来自分子间距离(气体之间就没有吸附力,除了气体了气体之间,其他两种介质之间接触都会有吸附力)

粘性宏观表现为流体之间的动摩擦力

牛顿流体的公式和胡克定律有相通之处,只适用于某个范围的分析
微观上粘性就是分子之间的作用力,速度不同的分子之间的化学键的变化,两层的分子之间的牵扯和挤压

微观上是分子的化学键的变化,流体分子的上下层存在 掺混作用

气体的粘性和分子的热运动有关,热运动越强粘性越大,可看不同温度的粘性
有两种粘性系数
动力粘性系数和运动粘性系数
在水中阻力大主要是水的密度大
水和空气的粘性比较要在相同加速度时比较,加速度体现了流体的运动方式
考虑流体自身的运动,要看运动粘性系数,水的粘性比空气的粘性还小一点,水和空气的运动粘性粘性系数相差不多


当流体发生连续剪切变形时产生粘性剪切力

机翼表面的分子被粘在表面,离机翼较远的地方保持较高的速度 机翼那里有很大的速度梯度,分为有粘区和无粘区

流线型的机翼有表面压力在流动方向的分量(压擦阻力)+摩擦力
阻力和粘性的关系很复杂

大铁球和小铁球下落,小铁球下落的更慢,因为小铁球粘性作用更明显
流体的可压缩性
受外界压力时体积减小的容易成都

压缩性对固体没什么意义
液体的密度不随温度变化
等温压缩比等商压缩更容易些

气体只有在外界有压力时才存在,没有压力就四散开来了

压缩问题,弹力来自两端的速度不同

声音在流体中传播是靠流体的压缩性,上流速度比下流速度大,下流逃跑速度最快就是音速,产生压缩,马赫数比较大时气体对压缩性是不能忽略的

流体加速运动就是膨胀的

纵向压差力平衡重力,横向压差力平衡惯性力
不可压缩气体不是理想气体,真实气体都很接近理想气体
不可压缩流体的密度是一个常数
流体的温度受到摩擦和换热的影响,可压缩流体有总温和静温之别,不可压缩流动总温=静温

不可压缩流动,各种方程都有一定程度的简化,更易做理论分析,不可压缩无摩擦时机械能守恒,动量和能量可以分开考虑
收缩使得气流加速是对应亚音速的情况,流动为超音速时情况正好相反,收缩使气流减速

跑的太快了,收缩堆积,堆积后使收缩后的气流减慢,汽车的运动到窄扣,下游的减速通知不到上游导致堵车一个道理
两端一样大也有可能出现流速不相同的情况,有可能进口给了一个力然后导致上游速度很快产生堆积,对可压缩流体而言
气体减速时被压缩,导致温度会上升
气体的压缩性是热机工作大基础,技术功来源就是气体的膨胀功,燃气轮机是开式大,开式工作必须高速运动,内燃机是封闭环境下运行的可以低速运动
超音速气流减速产生激波,激波是强压缩波,突气流然减速,压力升高,声音就是一种压力波,激波是可以被听到的,爆炸时也会产生激波,非常响

内燃机工作可以低速,因为是封闭环境
流体静力学

浮力定律:液体中物体受到大浮力等于排开水的重量
这门课的压力=压强(应力)

水下压力公式

静止的流体内部没有剪切力
只有压力和质量力
表面力,作用在接触面的力,表面力的合力一般是指压力在表面力上对封闭积分
质量力,作用在质量的力

同样的深度朝任何方向的压力都相同,压力和深度的关系可以类比小球堆叠

桶裂实验垂直的压力会转换成四面八方的压力
通用方程
表面力与质量力平衡


推广到三维可以看到,压力是由质量力产生的,压力沿质量力方向增加

只要流体内部没有相对运动,静力方程就是成立的
加速度不变,流体才不变形
考虑惯性力的流体静力学问题为以下两类


流体质点的运动
时间、位置、质点、速度和加速度
研究质点的运动一般是采用拉格朗日法
流体微团长得都一样,比较偏向于使用空间的欧拉法
流体的流速有可能出现没有加速度却有速度改变

空间某点对流速随时间变化对现象叫做流动对非定常性,表示为速度对时间对偏导数
定常流动,流线和迹线重合
流线:每一点都与当地速度矢量相切的曲线(同一时刻,不同流体质点的速度情况)
迹线:流体质点在空间中运动时所经过的轨迹曲线(不同时刻同一流体质点的运动)
气体不一定按照流线运动,同一点触发对质点可能按照不同的流线图运动

速度对时间的倒数是 当地加速度,表示流动的非定常性
可以理解为,这个地方,速度随时间的变化
速度随位置的变化表示了流动的不均匀性,表示的是对流加速度,流场的非均匀性,他们都不是质点那个意义的加速度,这里的
表示的是全导数,时间的变化+空间的变化,也称材料导数

下面的ax ay等等是分量加速度
水段自由下落,空间中某点的速度是一直增加的,则$ \frac{\partial u}{\partial t} \(!=0,但是由于一起下落,各点速度一致,则\) \frac{\partial u}{\partial x} $=0
无限大水箱排水,管道处的排水速度不变,则属于定常流动,排水速度有变化就是非定常流动(水面下降排水速度下降,当地加速度小于0)

欧拉法研究空间点,质点和空间点的转变需要一个关系
空间点表示的是不同时刻在这个位置的不同质点的变化,质点则只关注自己不同时刻的变化
这里的导数称为随体导数,也称材料导数,反映了物质随时间的变化和随空间对变化,当地项和对流项

流体微团的运动

收缩通道变形,微团的运动可分解为很多基本运动,变形的原因是微团各个位置的速度不一致造成的

平动、转动、变形,平动可当做质点


线变形问题,单位时间的相对伸长量就是变化率,多方向的先变形的叠加

单位时间内体积的相对变化量,矢量表示,这个表达式表示速度的散度

均匀膨胀只有线变形 是否有角变形和是否有角度变化有关
牛顿实验的运动有剪切和旋转两个运动

图里下边是微团旋转运动公式的推导,线速度除旋转半径可得到旋转角速度,然后求一下两个极限的平均
压力导致膨胀和收缩
粘性力是导致剪切和旋转的原因
流动中质量守恒
一维流动质量守恒

欧拉的质量守恒分析空间里的流出流入

不可压流动的流体微团的体积变化为零,各方向速度在各方向的梯度为0
矢量形式对倒三角称为:Nabla算子 看起来含义为各个分量在各个方向上的偏导数,含义为一个偏导数组成的向量,其实就是梯度
连续性方程本质上是质量守恒,质量等于密度乘以体积,速度散度的物理意义是流体微团的可压缩性。散度为0则表明流体不可压缩。
关于散度为0流体不可压缩的解释:单位体积的流体微团不会有流入或流出的量,如果有那么会导致压缩或膨胀(这点和不可压缩性冲突),这个流入和流出体积变化对应的就是单位体积两面流速变化,也就是速度矢量的单位体积通量为0
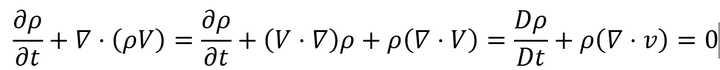
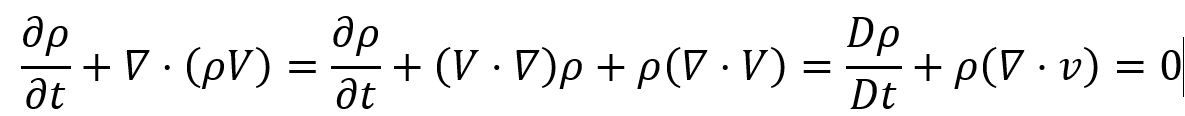
当流体微团不可压缩时表明流体密度保持不变,即密度的物质导数为0,此时根据上式速度散度为0,表明流体不可压缩。
下面质量守恒的式子力有速度散度项,表示的是微团体积的变化,乘上密度表示体积影响的微团质量的变化
密度的材料导数表示流体微团密度变化导致的微团质量变化

收缩运动至少是二维的

不同速度的流体的收缩加减速情况不同,超音速空气放大口加速
密度的变化比速度的变化大
汽车的速度运动较慢,属于不可压缩流动

当容腔只有一个开口,气流会在开口处形成很强的非定常流动(同一位置的流体速度会随时间滨化),所以会感觉到窗边有风


坡度决定流速?
流速决定横截面积

小孔位置压强低,有压强差推动流体加速(这里的问题是先有压差导致的加速,还是有速度不一致导致了压差)

加速就是因为质量守恒,不可压缩,密度为常数,面积减小,速度就变大了
流动中对动量定理
小孔加速是流体微团受到的压差力而加速


气球 air下标表示一个总的动量变化
发动力受到吊架对他的向后的推力,因为发动机给飞机向前的推力,发动机只受这一个推力T,所以气流的动量变化产生的力应当同这个T相同
升力导致空气有向下的运动趋势


斯托克斯在牛顿粘性力公式的基础上通过一定合理的假设,得到广义牛顿粘性力公式,也称为本构方程
NS方程 这里是矢量形式的动量方程
粘性力简化掉就可得到欧拉方程,流体是静止的,得到惯性力为0

(这块还需要看看书)伯努利方程的条件是 定常无粘不可压并且沿一条流线
无限长管道流动的解析解 解 管内流速分布 第三个条件是无滑移条件
流体流速沿流动方向不变,压差力和剪切力平衡
最大速度是平均速度的两倍
得到单位长度压降和管径的关系
这种流动是少数得到解析解的流动
流动中的能量守恒
热力学第一定律
吸热则Q为正,对外做功W为正

开放系统的热力学定律体现有所不同,系统从外界吸热为正,系统对外界做功为正(在物理角度的定义和化学角度的定义不一样,化学角度将系统对外做功定义为负)
流量 = $ \rho AV$
粘性力不做功,因为和壁面接触的流体没有相对运动
v是密度的倒数
轴功通过往复运动来施加,和为定常流动游有关
m的导数就是流量的意思

焓表示中的流动功可以理解为压力势能,重力做功影响重力势能,方程右边表示流体与外界的换热及能量交换
粘性影响能量方程需要通过微分形式才能看出来
流体微团在外表面上推动邻近的流体做功,就是表面力做功



张量形式的能量方程
切应力还需要带入本构方程去计算
能量方程的解释

张量使用下标表示
变量有一个下标那么他就表示一个矢量,比如图里的 \(f_i\) z这个下标是自由下标,意思该坐标有3个坐标分量
相同的单下标相乘表示矢量的点乘
当一个变量有两个下标就表示他有9个分量

表面力推动流体微团平动

总能量方程和动能方程相减得到内能方程
表面力做的功也改变内能,通过流体微团变形产生的


二维变形功:

表面力分为压力和粘性力项,粘性力项写为耗散项,永远为正,这一项是动能不可逆的转化为内能
压力导致的功就是体积功,体积功是可逆的

熵和内能的关系
熵增 = 吸热+耗散


焓方程+动能方程=总焓

轴功是什么?非定常压力做功+耗散,叶片通过旋转对流体做功,叶片给流体增加非定常压力,轮毂对流体通过粘性力做功(基本体现为损失)

伯努利方程
无粘区流动没有连续剪切变形

沿流向压力下降温度上升




流动方程的解

部分流动有微分方程特解

泊肃叶流动

解可能不唯一
流动状态:层流、湍流
湍流没有规律

什么决定了流态

计算的雷诺数和扰动有关
雷诺数2300-4000为中间状态,不稳定
稳定性:系统抵抗小扰动而保持某种状态的能力
稳定性理论只对线性系统才严格成立





扰动越大越易转捩

湍流的抗分离能力强,可以减小小球的启动阻力
尾流一般是湍流,这种转捩就是分离转捩

正确利用分离泡现象可以降低阻力

射流:往一个流体中射另一个流体
雷诺数和马赫数


这里只是借用亚里士多德,并无关系,效果就是有点力都被粘性力平衡了


阻力不只是粘性力
流体与球表面有摩擦力
速度快起来会有非定常流动

卡门涡街 中等雷诺数下,流体绕过球后形成规则的脱落涡,搜到阻力+周期性的横向激振力


低雷诺数下,粘性力大,动能转换快,大部分都是小涡

选择边界层厚度也可行为特征尺度也可以


音速并不是常数,马赫数不能直接用来判断速度大小

亚音速范围阻力系数随马赫数增大而增大

人类的活动范围和伯努利原理的描述范围相交最多



 浙公网安备 33010602011771号
浙公网安备 33010602011771号